CF1638D - Big Brush（构造性算法 + 数据结构 + 贪心 + 模拟 / 铁牌级）
1638D - Big Brush（源地址自⇔CF1638D）
tag
⇔构造性算法、⇔数据结构、⇔贪心、⇔模拟、⇔铁牌级（*2000）
题意
在一张 \(N *M\) 的画布上涂颜色，规定涂色操作如下：
-
最初的画布是没有颜色的；
-
画笔一次性对 \(2*2\) 的正方形涂色——对于选中的 \((i, j)\) 位置，同时对 \((i+1,j)，(i,j+1)，(i+1,j+1)\) 涂上颜色；
-
保证所有的格子都会被涂上颜色，一个格子可以被多次涂色。
现在要求你找到一种可能的涂色方法，并且输出步骤（注意，不能超过 \(N*M\) 次）。
思路
概要：很容易的，可以找到最后一下涂色涂的位置，而这个位置下所掩盖的颜色是不确定的，所以，我们发现可以通过逆推找到涂色的顺序。
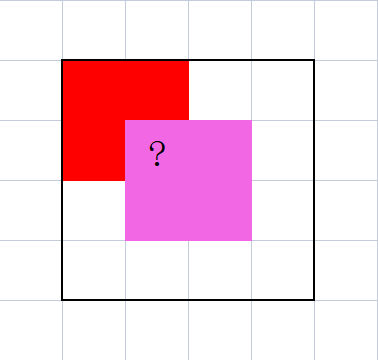
不妨将被掩盖的格子定义为“万能格”，这些格子的颜色可以通过边上的格子来确定（如图，我们可以通过三块红颜色的格子推断“？万能格“的颜色也为红色）。那么相应的，只需要暴力枚举每一种情况，就一定能得到一种可行解。模拟分析后可以知道，对于下方粉色的”万能格“，至多需要枚举 \(8\) 种情况，而这样的万能格数量至多为 \(N*M\) 个，故该算法的复杂度为 \(\mathcal{O}(N*M)\) ，可解。
AC代码
点击查看代码
//====================
int n, m, a[1010][1010];
bool Ans;
vector<tuple<int, int, int> > ans;
queue<pair<int, int> > q;
//====================
void check(int x, int y) {
if(x < 1 || x >= n || y < 1 || y >= m) return;
if(a[x][y] + a[x + 1][y] + a[x][y + 1] + a[x + 1][y + 1] == 0) return;
int color = max(a[x][y], max(a[x + 1][y], max(a[x][y + 1], a[x + 1][y + 1])));
if(a[x][y] != 0 && a[x][y] != color) return;
if(a[x + 1][y] != 0 && a[x + 1][y] != color) return;
if(a[x][y + 1] != 0 && a[x][y + 1] != color) return;
if(a[x + 1][y + 1] != 0 && a[x + 1][y + 1] != color) return;
q.push({x, y});
}
void Clear() {
}
void Solve() {
cin >> n >> m;
FOR(i, 1, n) FOR(j, 1, m) cin >> a[i][j];
FOR(i, 1, n - 1) {
FOR(j, 1, m - 1) {
if(a[i][j] == a[i + 1][j] && a[i][j] == a[i][j + 1] && a[i][j] == a[i + 1][j + 1]) {
q.push({i, j});
}
}
}
while(!q.empty()) {
auto [x, y] = q.front();
q.pop();
if(a[x][y] + a[x + 1][y] + a[x][y + 1] + a[x + 1][y + 1] == 0) continue;
int color = max(a[x][y], max(a[x + 1][y], max(a[x][y + 1], a[x + 1][y + 1])));
ans.pb({x, y, color});
a[x][y] = a[x + 1][y] = a[x][y + 1] = a[x + 1][y + 1] = 0;
check(x - 1, y - 1);
check(x - 1, y);
check(x - 1, y + 1);
check(x, y - 1);
check(x, y + 1);
check(x + 1, y - 1);
check(x + 1, y);
check(x + 1, y + 1);
}
FOR(i, 1, n) {
FOR(j, 1, m) {
if(a[i][j] != 0) {
cout << -1 << endl;
return;
}
}
}
reverse(ans.begin(), ans.end());
cout << ans.size() << endl;
for(auto [x, y, z] : ans) cout << x << " " << y << " " << z << endl;
}
错误次数
无。
文 / WIDA
2022.02.22 成文
首发于WIDA个人博客，仅供学习讨论
更新日记：
2022.02.22 成文
