CF1621D - The Winter Hike（构造性算法 + 贪心 + 数学规律 / 铜牌级）
1621D - The Winter Hike（源地址自⇔CF1621D）
tag
⇔构造性算法、⇔贪心、⇔数学规律、⇔铜牌级（*2100）
题意
一个 \(2n * 2n\) 的球形地图上有一些重量不一的雪堆，重量通过 \(c[1...2n][1...2n]\) 给出。现在，给出这张地图的平面样式，并给予每个格子唯一编号。在平面图左上角的 \(n^2\) 个格子里，每个格子都有一个小伙伴（即在每个满足 \(1 \le x,y \le n\) 的格子内都有一个小伙伴），你需要指挥他们到达地图右下角的 \(n^2\) 个格子，使得每个格子都有一个小伙伴（只要到达即可，顺序不做考虑），但是在路途中不能碰到雪堆。指挥规则如下：
- 选中一行，令这一行的所有人左（右）移一格。
- 选中一列，令这一列的所有人上（下）移一格。
- 地图是球形的，走到边界的小伙伴会从另一端出现（例如，令位于第 \(2n\) 列的小伙伴右移一格，Ta会移动至第 \(1\) 列）。
在指挥前，你可以删去任意重量的雪堆，以便完成你的指挥。保证 \(1 \le x,y \le n\) 的格子内没有雪堆，请你求出你需要删去的雪堆重量的最小值。
思路
首先显然的，右下角所有格子的雪堆必须要删去。
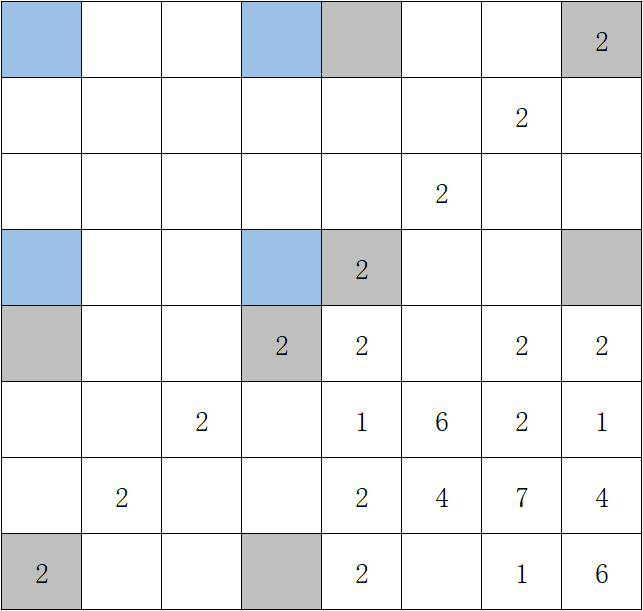
其次，我们考虑左上角四个边界处的小伙伴（他们分别位于 \((1, 1)，(1, n)，(n, 1)，(n,n)\) ，如下图，用蓝色标注），而我们发现，只要对第 \(1\) 行、或第 \(n\) 行、 或第 \(1\) 列、或第 \(n\) 列进行一次操作，这四个小伙伴必定有一个会被移动到左上角的安全区域之外（如下图，用灰色标注）——所以，我们至少应该移除这八个灰色格子中的一个的雪。而一旦这么做了，左上角与右下角就被打通了，可以证明。所有的小伙伴都可以通过这个格子到达右下角的区域并且做到每个格子一个。
AC代码
点击查看代码
//====================
LL n, ans, num, a[505][505];
bool Ans;
//====================
void Solve() {
cin >> n;
FOR(i, 1, 2 * n) {
FOR(j, 1, 2 * n) {
cin >> a[i][j];
if(i > n && j > n) ans += a[i][j];
}
}
num = MAX18;
num = min(num, a[1][n + 1]);
num = min(num, a[1][2 * n]);
num = min(num, a[n][n + 1]);
num = min(num, a[n][2 * n]);
num = min(num, a[n + 1][1]);
num = min(num, a[n + 1][n]);
num = min(num, a[2 * n][1]);
num = min(num, a[2 * n][n]);
cout << ans + num << endl;
}
错误次数
无
文 / WIDA
2022.01.18 成文
首发于WIDA个人博客，仅供学习讨论
更新日记：
2022.01.18 成文
