CF1269D - Domino for Young（数论 + 组合数学 + 构造性算法 / 铁牌级）
1269D - Domino for Young - （源地址自⇔CF）
tag
⇔数论、⇔组合数学、⇔构造性算法、⇔铁牌级（*2000）
题意
给出一张有 \(n\) 列的直方图，从左至右高度非递增。现在要用 \(2 * 1\) 或 \(1 *2\) 的多米诺骨牌覆盖这张图，求解最多可以放置多少个多米诺骨牌。
思路
结论法
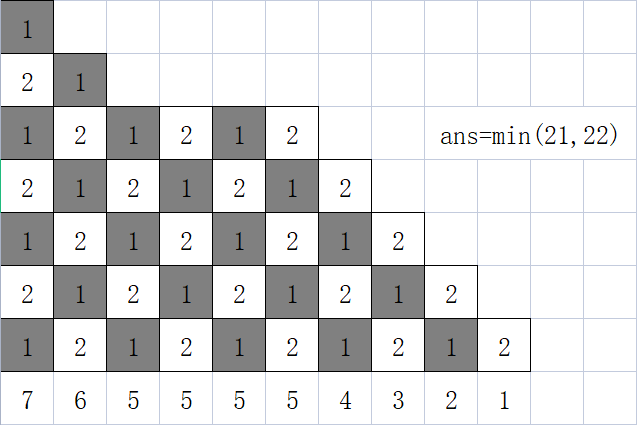
《组合数学》黑书第一章第一节提及了这一种做法——将图染上黑白两色，只需使得相邻方格颜色不同，答案即为 \(min(\) 染黑色方格数，染白色方格数 \()\) 。部分原理解释：一个多米诺骨牌必然会覆盖一黑一白两个方格，故答案数量即为颜色方格数量。【不能解释的原理：为什么需要保证直方图是非递增的才可以使用该方法？】
自己推导的方法
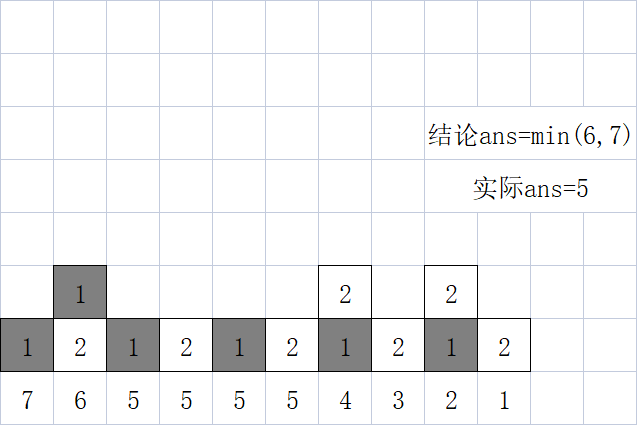
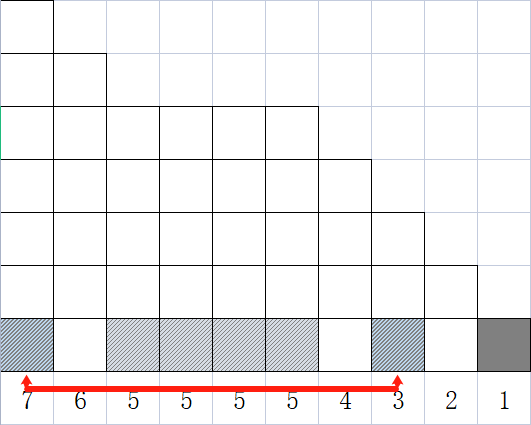
我们发现，只要我们对于每一列都从上往下竖放多米诺骨牌，最终会得到两个可能的结果：恰好放满这一列、剩余一个格子未被放置。而我们要特殊处理的就是这些多余的格子：归纳总结可以发现，对于多余的那个格子，只要有另一个多余格与其相距偶数个格子，这两个多余格便可以配对。
AC代码（结论）
点击查看代码
void Solve() {
LL num1 = 0, num2 = 0;
cin >> n;
FOR(i, 1, n) {
cin >> x;
if(i % 2 == 0) {
num1 += (x + 1) / 2;
num2 += x / 2;
}else {
num2 += (x + 1) / 2;
num1 += x / 2;
}
}
cout << min(num1, num2) << endl;
}
AC代码（自己推导）
点击查看代码
void Solve() {
LL x;
cin >> n;
FOR(i, 1, n) {
cin >> x;
ans += x / 2;
if(x % 2 == 1) {
if(S.empty() || (i - S.top() - 1) % 2 == 1) {
S.push(i);
}else if((i - S.top() - 1) % 2 == 0) { //与相邻的多余格相差偶数个格子
S.pop(); //配对并弹出
ans ++;
}
}
}
cout << ans << endl;
}
错误次数
（补题）自己推导的时候没有意识到最后一张图中标注的两个多余格也可以配对。
（补题）爆int。
文 / WIDA
2022.01.12 成文
首发于WIDA个人博客，仅供学习讨论
更新日记：
2022.01.12 成文
