CF161A - Dress'em in Vests!（暴力+贪心/二分/普及级）
161A - Dress'em in Vests!（源地址自⇔CF161A）
Problem
tag：
⇔暴力、⇔贪心、⇔二分、⇔普及级（*1300）
题意：
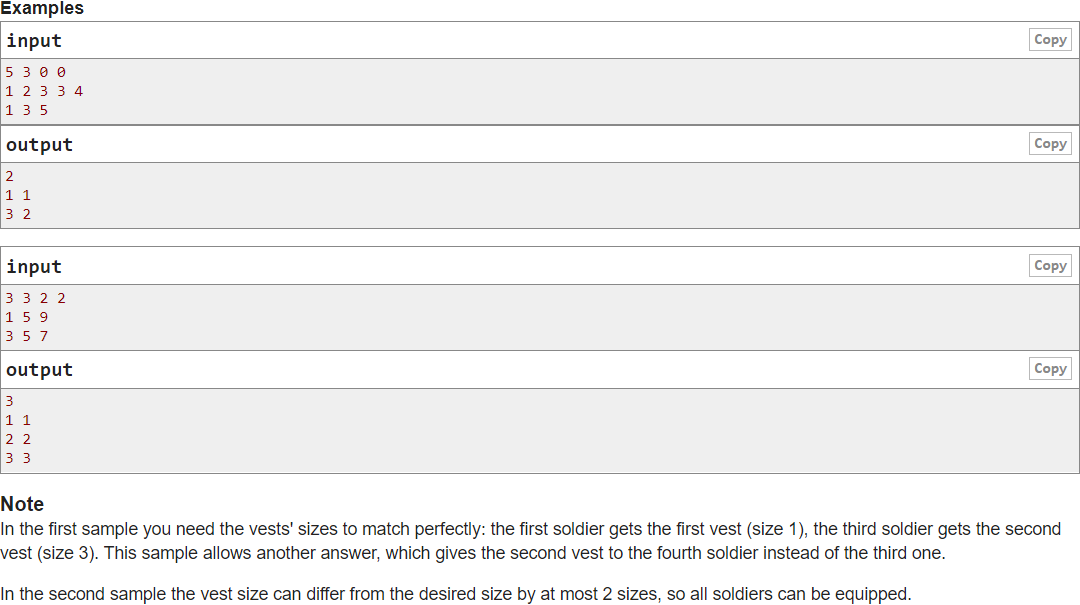
有 \(n\) 个士兵和 \(m\) 件背心，给出每个人的体型 \(a_i\) 和每件背心的大小 \(b_i\) ，当满足 \(a_i-x\leq b_j\leq a_i+y\) 时，说明第 \(j\) 件背心可以被第 \(i\) 个人穿上。使得尽可能多的士兵穿上背心，并输出这些匹配对。
思路1【二分】：
对于第 \(i\) 个士兵，二分查找可供挑选的背心，找到刚好穿上的那一件 \(b_j\) 。由于数据有序，对于下一个士兵 \(i+1\) ，他刚好能穿上的那一件大小必定大于 \(b_{j+1}\) ，故二分查找可供挑选的背心，范围是 \(j+1\) 到 \(m\) 。时间复杂度 \(O(n*log_2m)\) 。
思路2【暴力】：
上方的思路已经提到了查找范围的变化，而由于数据是有序的，只要遍历就可以。
对于第 \(i\) 个士兵，顺序查找可供挑选的背心，找到刚好穿上的那一件 \(b_j\) 。由于数据有序，对于下一个士兵 \(i+1\) ，他刚好能穿上的那一件大小必定大于 \(b_{j+1}\) ，故继续顺序查找可供挑选的背心，范围是 \(j+1\) 到 \(m\) 。时间复杂度 \(O(n+m)\) 。
AC代码1【二分】：
//A WIDA Project
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX=1e6+5;
LL n, num, m, x, y, w, ans[MAX], Ans[MAX], start = 1, M[MAX], N[MAX], t;
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n >> m >> x >> y;
for(int i = 1; i <= n; i ++) cin >> N[i];
for(int i = 1; i <= m; i ++) cin >> M[i];
for(int i = 1; i <= n; i ++) {
t = lower_bound(M + start, M + 1 + m, N[i] - x) - M;
if(M[t] <= N[i] + y && M[t] != 0) {
num ++;
ans[num] = i;
Ans[num] = t;
start = t + 1;
}
}
cout << num << endl;
for(int i = 1; i <= num; i ++) cout << ans[i] << " " << Ans[i] << endl;
return 0;
}
AC代码2【暴力】：
//A WIDA Project
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX=1e6+5;
LL n, num, m, x, y, w, ans[MAX], Ans[MAX], start = 1, M[MAX], N[MAX], t;
int main() {
cin >> n >> m >> x >> y;
for(int i = 1; i <= n; i ++) cin >> N[i];
for(int i = 1; i <= m; i ++) cin >> M[i];
for(int i = 1; i <= n; i ++) {
while(start <= m && M[start] < N[i] - x) start ++;
if(start <= m && M[start] <= N[i] + y) {
num ++;
ans[num] = i;
Ans[num] = start;
start ++;
}
}
cout << num << endl;
for(int i = 1; i <= num; i ++) cout << ans[i] << " " << Ans[i] << endl;
return 0;
}
错误次数：7次【补题：3次】
原因：背心使用后没有更新新的查找范围，重复计算了 \(b_j\) ，而不是从 \(b_{j+1}\) 开始计算，WA。
原因：背心未被使用时（即某一士兵穿不上所有的背心）没有更新新的查找范围，TLE。
原因：背心使用后，更新新的查找范围多计算了一件，导致从 \(b_j+2\) 开始查找，而不是从 \(b_{j+1}\) 开始计算，WA。
原因：（同第一次）
原因：（同第二次）
原因：（本质上和第二次一样，略加了优化，但没有修改到本质，依旧TLE）
原因：二分范围取错，取了士兵的范围进行二分，而不是背心的范围，WA。
文 / WIDA
2021.11.6成文
首发于WIDA个人博客，仅供学习讨论
更新日记：
2021.11.6 成文
