CF1372B - Omkar and Last Class of Math（贪心+数学规律+数论+普及级）

CF1372B - Omkar and Last Class of Math（源地址自⇔CF1372B）

Problem

Example

3
4
6
9

2 2
3 3
3 6

tag：

⇔贪心、⇔数学规律、⇔数论、⇔*1300

题意：

将题目给定的 \(c\) 拆分成 \(a+b=c\)，求出使得 \(LCM(a,b)\) 最大的 \(a\) 与 \(b\)。

思路：

暴力打表寻找规律，发现对于给定的 \(n\) ，求解出其最大因数 \(x\) ，而答案即为 \(x\) 与 \(n-x\) 。为了得到最大因数，我们只需要求出最小因数 \(p\) ， \(x\) 即等于 \(\frac{n}{p}\) 。

严格证明请参考官方题解：

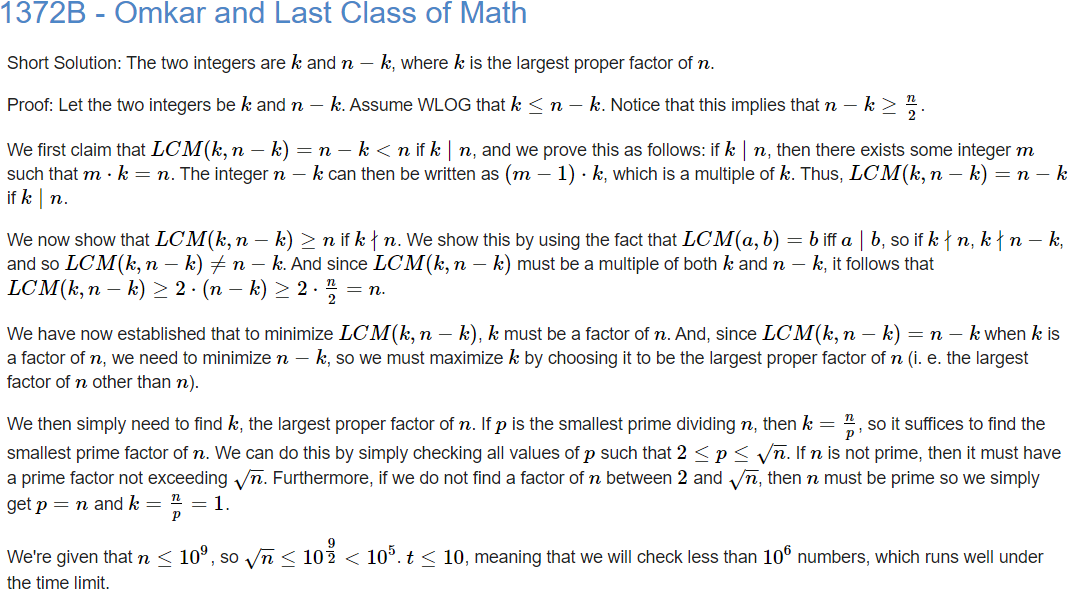
AC代码：

//A WIDA Project
#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL T,ans,n;
LL divi(LL n){
	for(LL i=2;i*i<=n;i++){
		if(n%i==0){
			ans=i;
			return ans;
		}
	}
	return 0;
}
int main(){
	ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
	cin>>T;
	while(T-->0){
		ans=0;
		cin>>n;
		ans=divi(n);
		if(ans==0) ans=n;
		else cout<<n/ans<<" "<<n-n/ans<<endl;
	}
	return 0;
}

错误次数：2次

原因：分解因数没有优化到 \(O(\sqrt{n})\) ，导致超时。

原因：未考虑给定的数字是质数的情况（最小因数为1，这种情况代码中ans=0），导致除以0的情况发生，RE一次。

---

文 / WIDA
2021.10.14成文
首发于WIDA个人博客，仅供学习讨论

---

更新日记：
2021.10.14 成文