二分图匹配——p3386 p2071 p2319 p1129(矩阵游戏)
---恢复内容开始---
二分图,就是给你一个图,可以将点分为两部分,每一部分的点都能唯一映射到另一个集合里,也就是有连边;
注:以下转自 http://blog.csdn.net/dark_scope/article/details/8880547
匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。匈牙利算法是基于Hall定理中充分性证明的思想,它是部图匹配最常见的算法,该算法的核心就是寻找增广路径,它是一种用增广路径求二分图最大匹配的算法。
-------等等,看得头大?那么请看下面的版本:
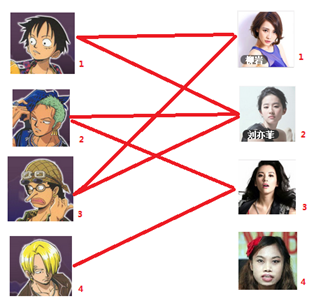
通过数代人的努力,你终于赶上了剩男剩女的大潮,假设你是一位光荣的新世纪媒人,在你的手上有N个剩男,M个剩女,每个人都可能对多名异性有好感( -_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉
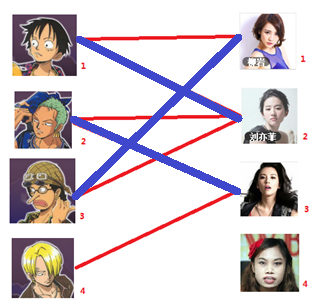
-_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉 ),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
===============================================================================
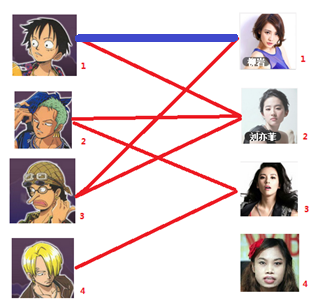
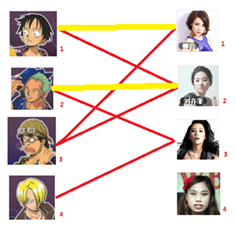
一: 先试着给1号男生找妹子,发现第一个和他相连的1号女生还名花无主,got it,连上一条蓝线
===============================================================================
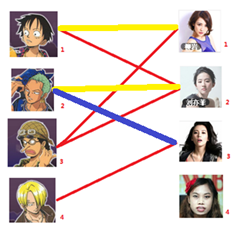
二:接着给2号男生找妹子,发现第一个和他相连的2号女生名花无主,got it
===============================================================================
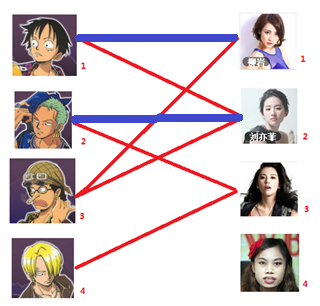
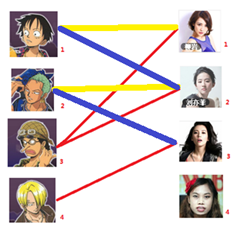
三:接下来是3号男生,很遗憾1号女生已经有主了,怎么办呢?
我们试着给之前1号女生匹配的男生(也就是1号男生)另外分配一个妹子。
(黄色表示这条边被临时拆掉)
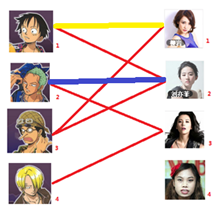
与1号男生相连的第二个女生是2号女生,但是2号女生也有主了,怎么办呢?我们再试着给2号女生的原配(
 )重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
)重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
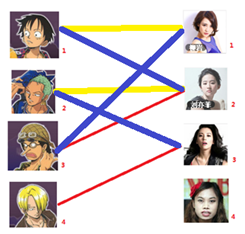
此时发现2号男生还能找到3号女生,那么之前的问题迎刃而解了,回溯回去
2号男生可以找3号妹子~~~ 1号男生可以找2号妹子了~~~ 3号男生可以找1号妹子
所以第三步最后的结果就是:
===============================================================================
四: 接下来是4号男生,很遗憾,按照第三步的节奏我们没法给4号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
===============================================================================
这就是匈牙利算法的流程,其中找妹子是个递归的过程,最最关键的字就是“腾”字
其原则大概是:有机会上,没机会创造机会也要上
这个讲的挺好的;
这个是模板,但是邻接矩阵应用限制大;
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=1010; int n,m,e; int edge[maxn][maxn]; int cp[maxn]; int ask[maxn]; int ans; bool search(int x) { for(int i=1;i<=m;i++) { if(edge[x][i]) { if(ask[i]) continue; ask[i]=1; if(!cp[i]||search(cp[i])) { cp[i]=x; return 1; } } } return 0; } void matching() { memset(cp,0,sizeof(cp)); for(int i=1;i<=n;i++) { memset(ask,0,sizeof(ask)); if(search(i)) { ans++; } } } int main() { scanf("%d%d%d",&n,&m,&e); for(int i=1;i<=e;i++) { int x,y; scanf("%d%d",&x,&y); if(x<=n&&y<=m) { edge[x][y]=1; //vis[y][x]=1; } } matching(); printf("%d",ans); return 0; }
P2071 座位安排
还是前式链向星舒服
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=5010; int n,m; int pre[maxn*2],last[maxn],other[maxn*2],l; void add(int x,int y) { l++; pre[l]=last[x]; last[x]=l; other[l]=y; } int ans,cp[maxn][5],ask[maxn][5]; //int ask2[maxn],cp2[maxn]; bool search(int x) { for(int p=last[x];p;p=pre[p]) { int v=other[p]; for(int i=1;i<=2;i++) { if(!ask[v][i]) { ask[v][i]=1; if(!cp[v][i]||search(cp[v][i])) { cp[v][i]=x; return 1; } } /*if(!ask2[i]) { ask2[i]=1; if(!cp2[i]||search(cp2[i])) { cp2[i]=x; return 1; } }*/ } } return 0; } void matching() { memset(cp,0,sizeof(cp)); for(int i=1;i<=2*n;i++) { memset(ask,0,sizeof(ask)); //memset(ask2,0,sizeof(ask2)); if(search(i)) { ans++; } } } int main() { scanf("%d",&n); for(int i=1;i<=2*n;i++) { int x,s; scanf("%d",&s); scanf("%d",&x); add(i,x); add(i,s); } matching(); printf("%d",ans); return 0; }
这个匈牙利算法我个人的理解就是先匹配,然后再递归替换;
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=2010; int n,m; int pre[maxn],last[maxn],other[maxn],l; int cp[maxn],ask[maxn]; void add(int x,int y) { l++; pre[l]=last[x]; last[x]=l; other[l]=y; } int ans; int num[maxn]; bool search(int x) { for(int p=last[x];p;p=pre[p]) { int v=other[p]; if(ask[v]) continue; ask[v]=1; if(!cp[v]||search(cp[v])) { cp[v]=x; num[x]=v; return 1; } } return 0; } void matching() { memset(cp,0,sizeof(cp)); for(int i=1;i<=n;i++) { memset(ask,0,sizeof(ask)); if(search(i)) { ans++; } else break; } } int main() { scanf("%d%d",&m,&n); for(int i=1;i<=n;i++) { int x,y; scanf("%d%d",&x,&y); if(x!=y) { add(i,x+1); add(i,y+1); } else add(i,x+1); } matching(); printf("%d\n",ans); for(int i=1;i<=ans;i++) { printf("%d\n",num[i]-1); } return 0; }
这几道题都是大同小异;
p1129矩阵游戏到是有点思维含量;
问是否可行,其实可以看出,就是行与列的匹配
如果g[i][j]==1,那么就给ij连一条边;
如果每行和每列都能成功匹配就是有解;
因为ij是1啊,如果这两个能匹配,这行和列都不能动,其他行只能找别的;
根据互换总能换成符合题意的形式;
(注意范围)
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=400; int t; int n,g[maxn][maxn]; int pre[maxn*maxn],last[maxn*maxn],other[maxn*maxn],l; void add(int x,int y) { l++; pre[l]=last[x]; last[x]=l; other[l]=y; } int cp[maxn],ask[maxn]; int ans; bool search(int x) { for(int p=last[x];p;p=pre[p]) { int v=other[p]; if(ask[v]) continue; ask[v]=1; if(!cp[v]||search(cp[v])) { cp[v]=x; return 1; } } return 0; } void matching() { memset(cp,0,sizeof(cp)); for(int i=1;i<=n;i++) { memset(ask,0,sizeof(ask)); if(search(i)) { ans++; } } } int main() { scanf("%d",&t); while(t--) { l=0;ans=0; memset(last,0,sizeof(last)); scanf("%d",&n); for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { scanf("%d",&g[i][j]); if(g[i][j]) { add(i,j); } } } matching(); if(ans==n) printf("Yes\n"); else printf("No\n"); } return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号