简单的整数划分问题——两个小时的死亡挣扎

 

将正整数n 表示成一系列正整数之和，n=n1+n2+…+nk, 其中n1>=n2>=…>=nk>=1 ，k>=1 。
正整数n 的这种表示称为正整数n 的划分。正整数n 的不同的划分个数称为正整数n 的划分数。

Input 标准的输入包含若干组测试数据。每组测试数据是一个整数N(0 < N <= 50)。 Output 对于每组测试数据，输出N的划分数。 Sample Input

5

Sample Output

7

Hint5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1

 

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int f[100][100];//和为i最大值为j
int main()
{
    for(int i=1;i<=55;i++) f[0][i]=1;
    for(int i=1;i<=55;i++)
    {
        for(int j=1;j<=55;j++)
        {
            if(i<j) f[i][j]=f[i][j-1];
            else if(i>j) f[i][j]=f[i-j][j]+f[i][j-1];
            else f[i][j]=1+f[i][j-1];//cout<<"i="<<i<<" "<<"j="<<j<<" "<<f[i][j]<<endl;
        }
    }
    
    while(scanf("%d",&n)!=EOF)
    {
        printf("%d\n",f[n][n]);
    }
    return 0;
}

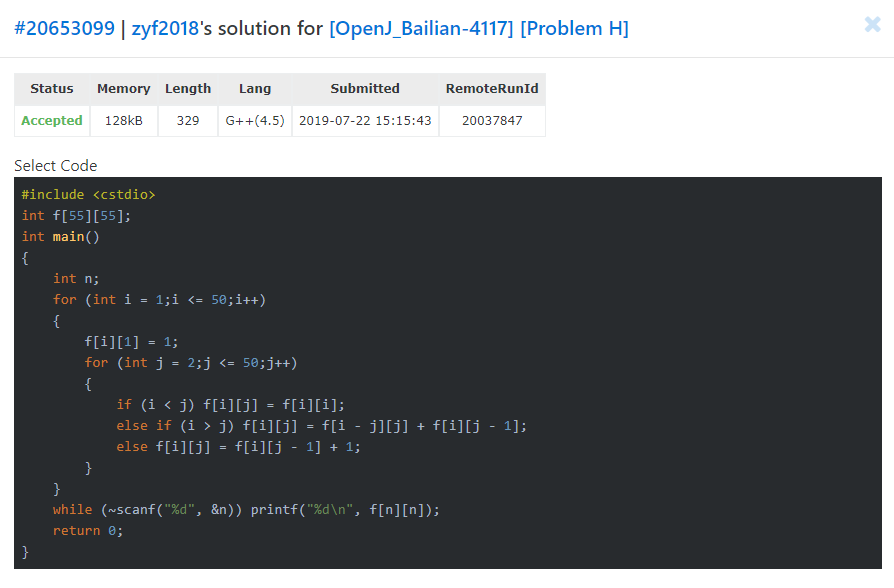
别人的代码……

天竹帮我找的代码写了一遍，应该是背包问题

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=60;
int n,f[maxn][maxn],ans;

int main()
{
    f[0][0]=1;
    for(int i=1;i<=55;i++)
    {
        for(int j=1;j<=i;j++)
        {
            f[i][j]=f[i-1][j-1]+f[i-j][j];
        }
    }
    
    while(scanf("%d",&n)==1)
    {
        ans=0;
        for(int i=1;i<=n;i++) ans+=f[n][i];
        printf("%d\n",ans);
    }
    return 0;
}

就是和为i中分出的集合分别计算最大值是j的情况数，因为我们是从小到大枚举，所以我们已经把前面的序列情况找到；

那怎么转移呢？为了不重复，我们要直接在已知的序列中加数，和为i可以从所有和为i-1最大值j-1的情况把最大值+1变成i,j;

也可以从和为i-j最大值为j的再加上j，最大值也没有变；

记住我们是一个个枚举的，最大值为1，最大值为2，最大值为3……