[CG] 二维变换

1 变换矩阵

平移矩阵

\[\begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x +t_x\\ y +t_y\\ 1 \\ \end{bmatrix} \]

缩放矩阵

\[\begin{bmatrix} s_x & 0 & 1\\ 0 & s_y & 1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} s_xx \\ s_yy \\ 1 \\ \end{bmatrix} \]

旋转矩阵

\[\begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} xcos\theta -ysin\theta\\ xsin\theta +ycos\theta\\ 1 \\ \end{bmatrix} \]

平移和缩放都很好理解，旋转矩阵可能要稍微推到一下，这里用到两角和差公式，如下：

\[\sin(\alpha\pm\theta) = \sin\alpha \cos\theta \pm \cos\alpha \sin\theta \\ \cos(\alpha\pm\theta) = \cos\alpha \cos\theta \mp \sin\alpha \sin\theta \]

P是旋转变换前的点，P'是旋转变换后的点，P与坐标轴的夹角为\(\alpha\)，P'与P的夹角为\(\theta\)，已知P的坐标和旋转的角度\(\theta\)

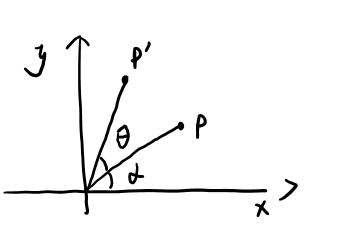
因为旋转前后P和原点的距离没有变化，所以设为\(\rho\)，则有

\[\rho\cos(\alpha+\theta) = x^{'}\\ \rho\sin(\alpha+\theta) = y^{'}\\ \rho\cos\alpha = x\\ \rho\sin\alpha = y\\ \]

利用两角和公式，即可得到

\[xcos\theta -ysin\theta = x^{'}\\ xsin\theta +ycos\theta = y^{'}\\ \]

上述的缩放也好，旋转也好都是相对于原点的，如果想相对于某个点进行缩放或者旋转，可以先把参考点平移至远点，然后再进行缩放或者旋转，完毕后，再平移回去。例如在坐标系中有一个矩形，我们想相对于它的中心进行缩放，和旋转，那么将其中心点平移至远点，然后进行缩放，然后再平移回去。
\(M_{composition} = A_{moveBack}A_{rotate}A_{scale}A_{moveToOrigin}P_{rect}\)

2 在WebGL中如何操作

在vertex shader中，对传入的顶点数据进行变换（乘变换矩阵），并赋给gl_Position

attribute vec2 a_position;
 
uniform mat3 u_matrix;//预先在js中计算出变换矩阵，然后传入shader中
 
void main() {
  // 使位置和矩阵相乘
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}

例如2D的投影矩阵，将像素空间转换为裁剪空间。像素空间默认的是原点在左上角，y轴朝下，坐标范围为[0,width]，[0,height]，而裁剪空间的原点在中心，y轴朝上，范围为[-1,1]。把在像素空间中定义的点，转换到裁剪空间中。

1. 将像素坐标缩放到[0,1]
2. 缩放到[0,2]
3. 坐标-1，变换为[-1,1]
4. 将y轴翻转

用变换矩阵来表示，就是

\[M_{projection}= \begin{bmatrix} 1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & -1\\ 0 & 1 & -1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 2 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} \frac{1}{width} & 0 & 0\\ 0 & \frac{1}{height} & 0\\ 0 & 0 & 1\\ \end{bmatrix} = \begin{bmatrix} \frac{2}{width} & 0 & -1\\ 0 & \frac{-2}{height} & 1\\ 0 & 0 & 1\\ \end{bmatrix} \]

所以在做变换的时候，可以基于像素坐标进行变换，最后再乘上投影矩阵，将像素空间变换到裁剪空间