石子合并(链+环)
链型 2021-12-27 17:21:53 星期一
链型
有N堆石子排成一排(n<=100),现要将石子有次序地合并成一堆,规定每次只能选相邻的两堆合并成一堆,并将新的一堆的石子数,记为改次合并的得分,编一程序,由文件读入堆数n及每堆石子数(<=200);
(1)选择一种合并石子的方案,使得做n-1次合并,得分的总和最少
(2)选择一种合并石子的方案,使得做n-1次合并,得分的总和最多
输入格式
第一行为石子堆数n 第二行为每堆石子数,每两个数之间用一空格分隔。
输出格式
从第1行为得分最小第二行是得分最大。
样例输入
4
4 5 9 4
样例输出
44
54
思路
在一定长度的下 更改起点终点 不断枚举分割点
代码
#include<bits/stdc++.h>
using namespace std;
int n,num[205];
int dp1[205][205],dp2[205][205],sum[205];
//dp1-min dp2-max sum-前i个石子数量和
int main (){
cin>>n;
for(int i=1;i<=n;i++){
cin>>num[i];
sum[i]=sum[i-1]+num[i];
}
for(int len=1;len<=n;len++){
for(int x=1;x<=n-len;x++){//起点
int y=x+len;//终点
dp1[x][y]=0x7fffffff;
for(int k=x;k<y;k++){// x<=k<y
dp1[x][y]=min(dp1[x][k]+dp1[k+1][y]+sum[y]-sum[x-1],dp1[x][y]);
dp2[x][y]=max(dp2[x][k]+dp2[k+1][y]+sum[y]-sum[x-1],dp2[x][y]);
}
}
}
cout<<dp1[1][n]<<endl<<dp2[1][n];
return 0;
}
环型 2021-12-30 17:04:56 星期四
环型
在一个园形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。 试设计出1个算法,计算出将N堆石子合并成1堆的最小得分和最大得分.
输入格式
数据的第1行试正整数N,1≤N≤100,表示有N堆石子.第2行有N个数,分别表示每堆石子的个数.
输出格式
输出共2行,第1行为最小得分,第2行为最大得分
样例
样例输入
4
4 4 5 9
样例输出
43
54
思路
破环成链
!!! 不能输出dp1[1][n] dp2[1][n]
因为最优解可以在整个环中任意一个长为n的链上
代码
#include<bits/stdc++.h>
using namespace std;
int n,num[205],sum[205],dp1[205][205],dp2[205][205];
int ddpp1=0x7fffffff,ddpp2;
int main (){
cin>>n;
for(int i=1;i<=n;i++){
cin>>num[i];
num[n+i]=num[i];//破环成链
//sum[i]=sum[i-1]+num[i];
//sum[i+n]=sum[i+n-1]+num[i];
}
for(int i=1;i<=n*2;i++){
sum[i]=sum[i-1]+num[i];
}
for(int len=1;len<=n;len++){
for(int x=1;x<=2*n-len;x++){
int y=x+len;
//cout<<"@@@"<<x<<" "<<y<<endl;
dp1[x][y]=0x7fffffff;
for(int k=x;k<y;k++){
// cout<<"!!!"<<k<<" "<<dp1[x][y]<<" "<<dp2[x][y]<<endl;
// cout<<dp1[x][k]<<" "<<dp1[k+1][y]<<endl;
// cout<<dp2[x][k]<<" "<<dp2[k+1][y]<<endl;
// cout<<sum[y]<<" "<<sum[x-1]<<" "<<sum[y]-sum[x-1]<<endl;
dp1[x][y]=min(dp1[x][y],dp1[x][k]+dp1[k+1][y]+sum[y]-sum[x-1]);
dp2[x][y]=max(dp2[x][y],dp2[x][k]+dp2[k+1][y]+sum[y]-sum[x-1]);
// cout<<"#"<<dp1[x][y]<<" "<<dp2[x][y]<<endl;
}
}
}
//for(int i=1;i<=2*n;i++){
// for(int j=1;j<=n*2;j++){
// cout<<setw(4)<<dp1[i][j]<<" ";
// }
// cout<<endl;
//}
for(int i=1;i<=n;i++){
ddpp1=min(dp1[i][i+n-1],ddpp1);
ddpp2=max(dp2[i][i+n-1],ddpp2);
}
//cout<<dp1[1][n]<<endl<<dp2[1][n]; 草率了
cout<<ddpp1<<endl<<ddpp2;
return 0;
}
四边形不等式优化 2021-12-30 17:47:03 星期四
优化
猜想
合并第i堆到第j堆石子的最优断开位置s[i,j]要么等于i+1,要么等于j-1,也就是说最优合并方案:
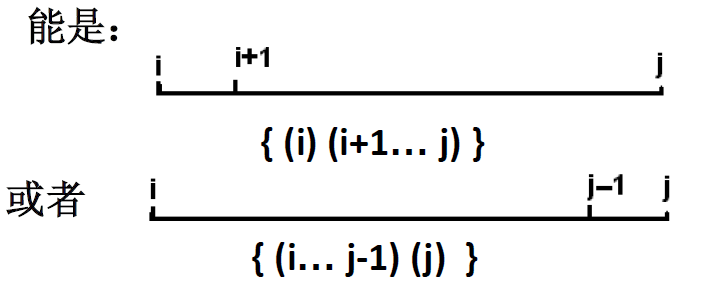
证明

#include<bits/stdc++.h>
using namespace std;
int n,num[4005],sum[4005],dp[4005][4005];
int ddpp;
int main (){
cin>>n;
for(int i=1;i<=n;i++){
cin>>num[i];
num[n+i]=num[i];
sum[i]=sum[i-1]+num[i];
}
for(int i=n+1;i<=2*n;i++){
sum[i]=sum[i-1]+num[i];
}
for(int len=1;len<=n;len++){
for(int x=1;x<=2*n-len;x++){
int y=x+len;
dp[x][y]=max(dp[x][x]+dp[x+1][y]+sum[y]-sum[x-1],dp[x][y-1]+dp[y][y]+sum[y]-sum[x-1]);//合并第i堆到第j堆石子的最优断开位置s[i,j]要么等于i+1,要么等于j-1
}
}
for(int i=1;i<=n;i++){
ddpp=max(dp[i][i+n-1],ddpp);
}
cout<<ddpp;
return 0;
}

