2016暑假集训第三次训练赛题解
A 火柴棒续
http://acm.fafu.edu.cn/problem.php?id=1665
肯定都会做。结果就是2n2+2n。
B 火柴棒再续
http://acm.fafu.edu.cn/problem.php?id=1666
很自然想到去解不等式2x2+2x<=n,求x的最大解,注意细节、sqrt精度那些问题了。有个取巧的方法是求出一个大概的值比如a,然后检查一下x分别等于...a+2、a+1、a、a-1、a-2...合不合法,因为求出大概的值后正确解就在这个值附近,这算是一个看起来挺low的技巧吧= =。。
也有一个很容易想到的思路就是枚举x,看看不等式是否成立,找到最大的x;虽然x最多只到20000多,不过这题说了数据有50000组是会超时的。
不过事实上可以发现如果一个解x=a成立,那么x=a-1也肯定成立,就是说这个解是具有单调性的,我们可以用二分去枚举这个解找到最大的解,即如果不成立x向左半区间找,而如果成立x向右边区间找。
求具有单调性的解的最值问题转化成二分枚举解的判定性问题,这是个常见的技巧。
C 迷宫的阿狸续
http://acm.fafu.edu.cn/problem.php?id=1667
直接BFS。。
当然我不会让你们无聊地一个个去搞那16个走法,注意到0到15这16个数字,它们代表着4个方向的所有组合,24种。
这时如果细心观察就会发现:这其实是把四个方向用四位二进制进行压缩,四个方向分别对应着四个二进制位;或者说一个点能走的方向集合用一个4位的二进制压缩了,二进制位为1表示该方向存在在集合中,0表示不存在。这种集合状态的压缩技巧很常见,比如状态压缩的动态规划。此外你们要熟悉位运算。
D 迷宫的阿狸再续
http://acm.fafu.edu.cn/problem.php?id=1668
题目相当于是,给一张点有权、边也有权的图,求1点到n点的最短路。
可以思考一下,把这张图转化成只有边带有权的图,这样直接跑那些最短路算法就OK了。转化的方式有两种:
第一种
考虑一下,从u点走到v点的情况(不考虑u点之前的情况):

可以发现花费是w+b,然后就显然了,即走过一条边产生的花费相当于边权与边的终点的点权的和。这样把边权和点权合并,简单转化后建图,跑最短路即可,记得加上源点1的点权。
第二种
把点一分为二,拆成两个点,中间连权为点权的边,如下:
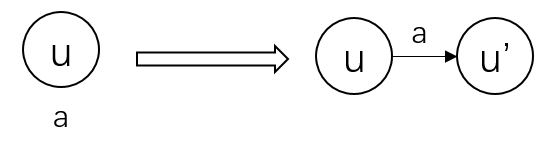
这样建图,走过一个点u,相当于必须走过u->u',于是利用拆点就把点权转化成边权了。事实上,这种拆点建图的技巧在图论的网络流中非常常见。
最后建完图就是跑最短路算法了,这题点和边都有10W个,权值也是正数,可以用堆优化的Dijkstra跑,其实也能用SPFA,简单好写。。
E Si: 渣神歿
http://acm.fafu.edu.cn/problem.php?id=1669
最朴素的解法是二重循环枚举i和j。。不过显然是会超时的。
考虑一下,如果确定了一边,比如i确定了或者j确定了,那么不就能直接求出另一边j或者i需要的aj或ai了嘛。那么直接枚举一边,然后求出另一边有多少个对应的a,累加各边贡献即可。
怎么求出另一边有多少个对应的a?直接用STL的map。map单次插入删除的时间复杂度是O(logn),于是这题就能在O(nlogn)解决。。如果你们还不知道STL的map、set这些容器做什么用的,百度一下。。
这种枚举一边,确定另一边,算是种思路吧。。
F Si: 彬神洽
http://acm.fafu.edu.cn/problem.php?id=1670
SG定理,打个表就知道了,偶数的SG值是1,奇数的SG值是0。SG值是这么求的:
#define MAXN 1111
int sg[MAXN]; bool vis[MAXN];
void get_sg(){
for(int s=1; s<MAXN; ++s){
memset(vis,0,sizeof(vis));
for(int j=1; j<s; ++j){
vis[sg[j]^sg[s-j]]=1;
}
for(int i=0; ; ++i){
if(!vis[i]){
sg[s]=i;
break;
}
}
}
}
G 周末娱乐
http://acm.fafu.edu.cn/problem.php?id=1671
首先要根据先序和中序序列建树,要保证建树的时间复杂度位O(n),而你们平时写的其实最坏情况是O(n2),因为先序各个点都会访问且只会访问一次,这是O(n);不过对于各个点都要找到在中序中的位置,这儿你们如果用循环,从中序区间开始位置到结束位置,去找的话每次最坏是O(n)的时间复杂度,这样总共就是O(n×n)的时间复杂度了(随机生成的树的期望高度可能大概是logn多几倍的水平吧,那样时间复杂度差不多就是O(nlogn)(主定理,T(n)=2T(n/2)+n => O(nlogn)),然而很容易造出一条链的数据使得时间复杂度为O(n2))。
做到O(n)很容易,只要找到在中序中的位置做到O(1)即可,注意到树的编号是1到n的,然后我不想多说什么了,一个简单的技巧即可,想一想。
建完树后,就是满足条件的点的数目了。其实相当于是有多少个点满足,它所有祖先中编号的最小值都比它的编号大。那么如何求所有祖先中编号的最小值?
考虑朴素的做法,记录每个点的父亲结点是谁,然后对于各个点,往上走一直记录最小值,直到到达树根。
这样对于树是一条链的情况显然是O(n2)的:
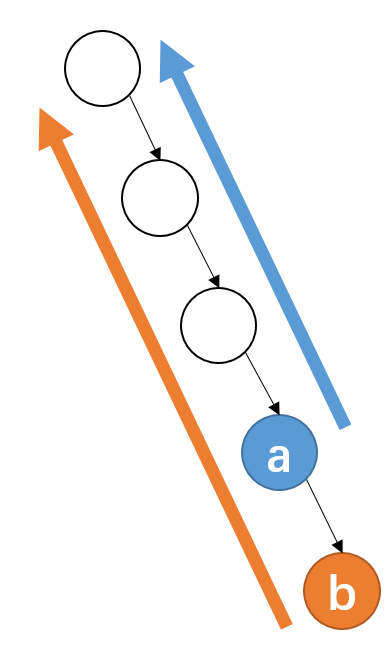
事实上可以发现这样有很多重复的计算。
比如算完a点,就能知道a点的往上祖先的最小值;而b点是a点的儿子,其祖先除了a点的所有祖先外,还有a点,而a点所有祖先的信息在计算a的时候就知道了,这完全没必要重复再往上走一遍,在a的祖先基础上加上a的信息就OK了。
那么实现的话,就是一个DFS的事情了,从根出发开始DFS,想想看怎么实现。如果对递归不熟悉的同学,还是要多练一练DFS,去理解递归、回溯的过程。
另外,这其实是个简单的树形动态规划,从树形DP的角度去理解:
- dp[u]表示 从u点到根路径上经过点的编号的最小值
- 考虑转移就是,dp[u] = min(dp[fa[u]], u)(fa[u]表示u的父亲结点)
这个很容易理解,具体实现也可以是一个DFS去转移这个方程。
当然树上面的算法很多,快速查询任意两点间链上的最小值,可以树链剖分+线段树,或者直接树上倍增,等等算法。。只不过画蛇添足,一个DFS,短短的几行,O(n)就能解决了= =。。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号