数学知识

整除

b | a：表示b 整除 a，即b是a的因数（存在一个整数q ， 使得a = qb）

---

 

素数

* 若 n 为合数 ，则n = ab 其中1 < a < n, 1 < b < n

定理

• 任何大于1的整数必有素因子
• 任何合数n都至少有一个不超过n^1/2的素因子
  • 判断n是否为素数：如果所有小于n^1/2的素数p都不能整除n 则n为素数

    int t = 2;
    for (int i = 2; i * i <= x; ++i)
        if (x % i == 0) {
             t = i;
             break;
        }
    if (x % t)
        t = x;  

     

• 算术基本定理　　
• 任何非零整数n ，可以表示成如下乘积形式
• n = p₁^k1p_2^k2 ....p_n^kn   其中p1，p2...pn 是互不相同的素数 ， k1，k2...kn是正整数
• 欧几里得定理
  
  • 素数有无穷多个

---

 

模运算

*a mod b = r  =>  a = qb + r

 有关负数取模：

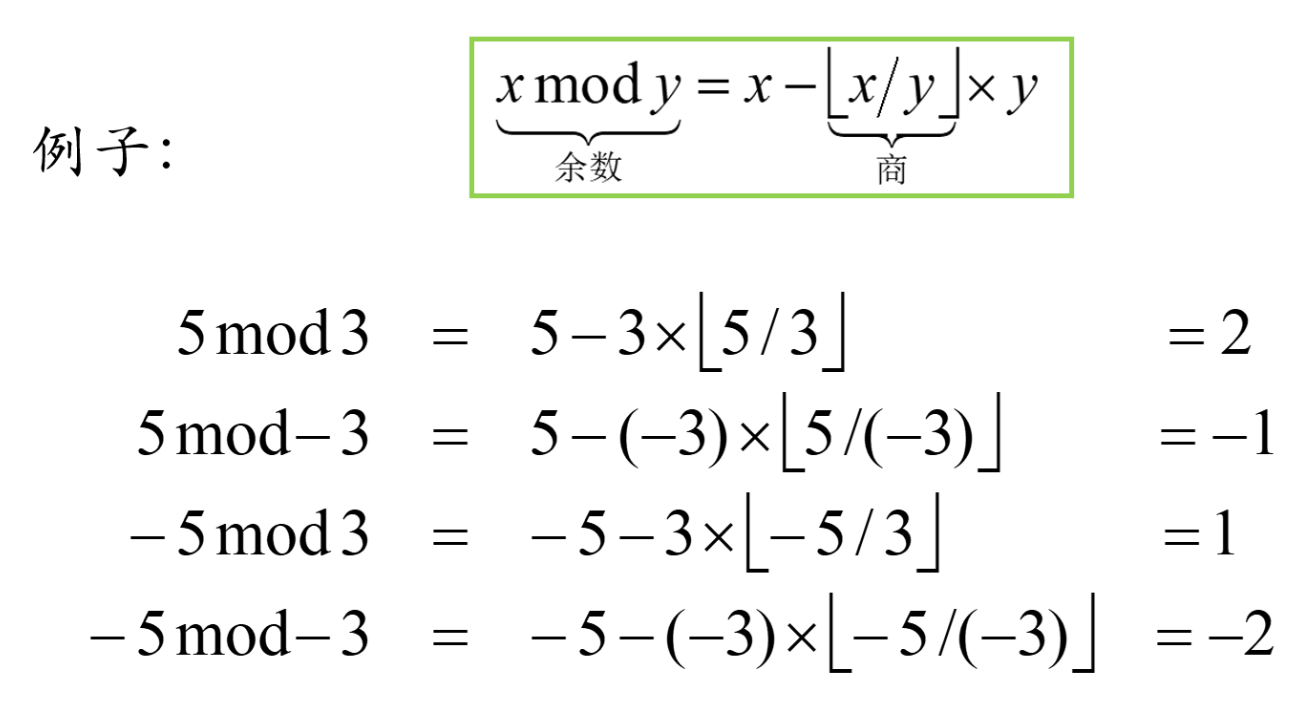
 性质

(a + b) mod n = (a mod n + b mod n) mod n

(a - b) mod n = (a mod n - b mod n  + n ) mod n   // 减法运算时可能出现负数 此时需要加上 n 

(a * b) mod n = (a mod n * b mod n) mod n

**除法没有该种性质

每一步计算都可以取模  最终结果不要忘了取模

 

---

 

最大公约数

a 与 b 的最大公约数为d 记作gcd (a , b)  = d

gcd ( a , b ) = 1 =>  a b 互素

性质

• 设 gcd (a , b ) = d  , a = q₁d  b = q₂d   则 gcd( q₁ ,  q2 ) = 1

 

• 最大公约数表示定理：
  • 设 gcd ( a , b ) = d ， 则存在x ，y ， 使得 ax + by = d  
  • 推论： d | v  ↔ ax + by = v
• 欧几里得算法
  • a = qb  +  r  则 gcd (a , b )  = gcd ( b, r  ) （辗转相除法）

  • // Version 1
    int gcd(int a, int b) {
          if (b == 0) return a;
          return gcd(b, a % b);
    }
    
    // Version 2
    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

• 扩展欧几里得算法
  • 　求不定方程 ax + by = gcd(a, b) 

    关于方程ax + by = k 给定a, b, k 的值 可以求出一组 x y 的解
     X = x * k / gcd(a, b)   
     Y = (k - a * x) / gcd(a, b)

  • int exgcd(int a, int b, int &x, int & y) {
        if (b == 0)  {
            x = 1;
            y = 0;
            return a;
         }
         int d = exgcd(b, a % b, x , y); 
         tie(x, y) = make_pair(y, x - a / b * y);
         return d;   // 返回值为是这组解(x, y)的最大公因数
    }
    
            

     

---

 

最小公倍数

a 与 b 的最小公倍数为m 记作 lcm(a , b)  = m

lcm ( a , b ) = a * b / gcd ( a, b )

另外，对于 C++14，我们可以使用自带的 __gcd(a,b) 函数来求最大公约数。而对于 C++ 17，我们可以使用 <numeric> 头中的 std::gcd 与 std::lcm 来求最大公约数和最小公倍数。

 

---

 

同余

同余：设整数 m ≠ 0 。若a 和 b 分别模 m 后得到相同的余数， 则称a 和 b 在模 m 下满足同余关系。简称同余。

定义 （同余关系）： 若 m | (a  - b ) ，称 m 为模数（模），a 同余于 b 模 m，b  是 a 对模m  的剩余。记作 a ≡ b ( mod m ) 。

运算性质： 

• a ≡ b ( mod m )  => a + c ≡ ( b + c ) ( mod m )
• a ≡ b ( mod m )  => a - c ≡ ( b - c ) ( mod m )
• a ≡ b ( mod m )  => a * c ≡ ( b * c ) ( mod m )
• a ≡ b ( mod m )  => a^c ≡  b^c ( mod m )
• a ≡ b ( mod m )   &&  c ≡ d ( mod m )  => a + c ≡ ( b + d ) ( mod m )   ( 两个式子相加减乘 同余结果也满足 ）

---

 

乘法逆元

定义：若 ax ≡ 1 ( mod m ) 则称 x 是模 m 下的乘法逆元  记作 a^-1 = x

eg ： （ 2 * 3 ） mod 5  =  1  ;  3 是模5 下 2 的乘法逆元

*注意点

• a 在模 m 内的乘法逆元 a^-1 是唯一的
• 乘法逆元存在的条件 gcd ( a, m )  = 1 ↔ 模 m 下， a 有乘法逆元
  • 模 4 下 ， 2 没有逆元

 求乘法逆元

•  扩展欧几里得算法

　　　　设 gcd ( a , m )  = 1

　　　　根据最大公约数表示定理 ， 有 ax + bm = 1；

　　　　等式两边同时模 m ， 得 ax ≡ 1 ( mod m )

　　　　易知 模 m 下 a 的逆元是 x　

　　　　

int exgcd(int a, int b, int &x, int & y) {
    if (b == 0)  {
        x = 1;
        y = 0;
        return a;
     }
     int d = exgcd(b, a % b, x , y); 
     tie(x, y) = make_pair(y, x - a / b * y);
     return d;   // 返回值为是模 b 下 a 的逆元
}