【学习笔记】基础算法:二次离线莫队/回滚莫队
【学习笔记】基础算法:二次离线莫队/回滚莫队
二次离线莫队
-
前置知识:莫队
-
前置知识:值域分块
值域分块,就是对 \(A\) 的值域进行分块,每个块维护该值域内数的个数
众所周知,莫队的复杂度是 \(O(n \sqrt m)\) 的,而在维护一些问题时左右端点移动一格并不是 \(\mathcal O(1)\) 的,此时朴素的莫队复杂度为 \(\mathcal O(kn\sqrt m )\)
如果我们对其进行二次离线,复杂度就会优化到 \(\mathcal O(nk+n\sqrt m)\) ,一般可以认为是 \(\mathcal O(n \sqrt m)\) 的
对于区间逆序对问题,有一个显然的莫队套树状数组做法,复杂度 \(\mathcal O(n \sqrt m \log n)\) (左右端点移动一格的复杂度为 \(\mathcal O(\log n)\)),原因很明显是因为每次询问我们都需要在树状数组上进行,左右移动一格需要在树状数组上 \(\log n\) 查询
但是如果我们使用 二次离线莫队 就可以优化到 \(\mathcal O(n\sqrt m)\)
区间逆序对问题
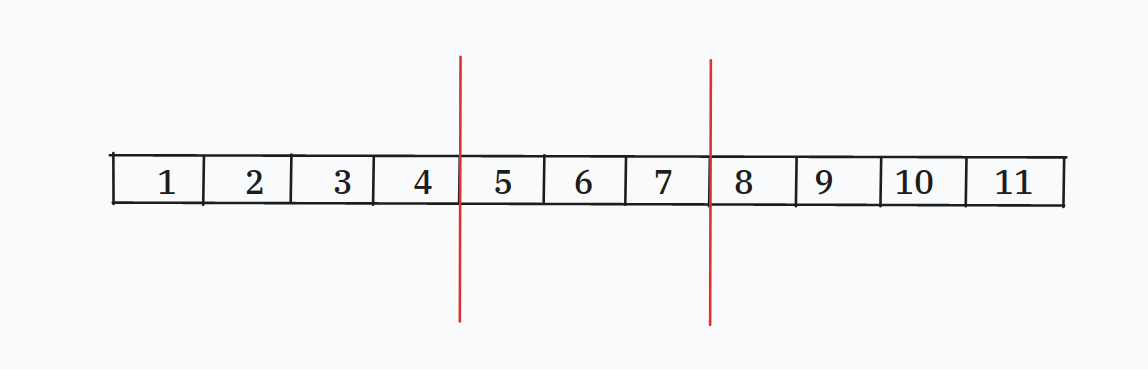
假设我们现在的区间是 \([l,r]\),也就是图中红色的部分
现在我们需要向右移动一格

这一次的移动为我们带来的贡献是 \([1\sim r]\) 内大于 \(\mathbf{val}(r+1)\) 的数量减去\([1\sim l-1]\) 内大于 \(\mathbf{val}(r+1)\)
用图中的数字来表示就是 \([1\sim 7]\) 内值大于 \(\mathbf{val(8)}\) 的数量 减去 \([1\sim 4]\) 内大于 \(\mathbf{val}(8)\) 的数量
考虑第一个(也就是 \([1\sim r]\) 内大于 \(\mathbf{val}(r+1)\) 的数量)是定值,可以直接预处理,但是在后面那个里 \(l\) 是不确定的,我们无法直接预处理,所以这个也就是主要要维护的地方
我们可以首先先对于每个位置都开一个 \(\mathbf{vector}\) 来维护,把当前询问的编号和 \(r+1\) 扔到 \(l\) 所在的 \(\mathbf{vector}\) 里,进行第二次离线
莫队一共会移动端点 \(\mathcal O(n\sqrt n)\) 次,内存较大
我们发现,从 \(r\) 移动到我们想要移动的 \(r_1\) 时 \(l\) 不会发生变化,所以我们可以直接把 \(\{r+1 \sim r_1\}\) 扔到 \(\mathbf{vector}\) 内,这样空间就是 \(\mathcal O(n)\) 的了
然后可以值域分块,单次 \(\mathcal O(1)\) 修改 \(\mathcal O(\sqrt n )\) 查询,但是我们发现我们有 \(n\sqrt n\) 次询问和 \(n\) 次修改
所以我们适当增加修改的复杂度至 \(\mathcal O(\sqrt n)\) ,借此将查询的复杂度降为 \(\mathcal O(1)\)
总复杂度 \(\mathcal O(n \log n+n \sqrt n)\),空间 \(\mathcal O(n)\)
练习题
-
P5047【YnOI2019 模拟赛】Yuno loves sqrt technology II
本题是二次离线莫队的板子题,查询区间逆序对,要求时间小于 \(\mathcal O(n^{\frac{3}{2}})\),空间 \(\mathcal O(n)\)
按照上面的区间逆序对问题来实现即可
特殊的,本题因为是 \(\mathbf{YnOI}\) 所以比较卡常,不能
#define int long long不然会TLEFastIO都救不回来那种点击查看代码
#include<bits/stdc++.h> #include <sys/mman.h> #define N 100010 #define firein(a) freopen(a".in","r",stdin) #define fireout(a) freopen(a".out","w",stdout); #define fire(a) firein(a),fireout(a) #define for_(a,b,c) for(int a=b;a<=c;a++) #define _for(a,b,c) for(int a=b;a>=c;a--) #define For_(a,b,c,d) for(int a=b;a<=c;a+=d) #define _For(a,b,c,d) for(int a=b;a>=c;a-=d) using namespace std; namespace Solve{ const char *I=(char*)mmap(0,1<<22,1,2,0,0); inline int read() { int x=0,f=0; while(*I<48)f|=*I++==45; while(*I>47)x=x*10+(*I++&15); return f?-x:x; } char O[1<<22],*o=O; void print(long long x) { if(x<0)*o++=45,x=-x; if(x>9)print(x/10); *o++=48+x%10; } struct Query{ int l,r,v,id; }q[N]; vector<Query> L[N],R[N]; int n,m,blo,a[N],b[N],c[N],d[N],mp[N],tot,pos[N],bL[N],bR[N]; long long sum1[N],sum2[N],ans[N],Ans[N]; inline bool cmp(const Query &a,const Query &b){ if((a.l-1)/blo!=(b.l-1)/blo) return (a.l-1)/blo<(b.l-1)/blo; return a.r<b.r; } namespace BIT{ #define lowbit(x) ((x)&(-x)) inline void Add(int x,int v){ For_(i,x,n,lowbit(i)) b[i]+=v; } inline int Ask(int x){ int ans=0; _For(i,x,1,lowbit(i)){ ans+=b[i]; } return ans; } } using namespace BIT; inline void Solve(){ sort(q+1,q+m+1,cmp); q[0].l=1; for_(i,1,m){ ans[i]=sum1[q[i].r]-sum1[q[i-1].r]+sum2[q[i].l]-sum2[q[i-1].l]; if(q[i-1].r<q[i].r) { L[q[i-1].l-1].push_back({q[i-1].r+1,q[i].r,-1,i}); } if(q[i].r<q[i-1].r) { L[q[i-1].l-1].push_back({q[i].r+1,q[i-1].r,1,i}); } if(q[i].l<q[i-1].l) { R[q[i].r+1].push_back({q[i].l,q[i-1].l-1,-1,i}); } if(q[i-1].l<q[i].l) { R[q[i].r+1].push_back({q[i-1].l,q[i].l-1,1,i}); } } } void In(){ n=read(),m=read(); blo=sqrt(n)+1; for_(i,1,n) { a[i]=read(); mp[i]=a[i]; } sort(mp+1,mp+n+1); tot=unique(mp+1,mp+n+1)-mp-1; for_(i,1,n) a[i]=lower_bound(mp+1,mp+tot+1,a[i])-mp; for_(i,1,n){ sum1[i]=sum1[i-1]+i-1-Ask(a[i]); Add(a[i],1); } memset(b,0,sizeof(b)); _for(i,n,1){ sum2[i]=sum2[i+1]+Ask(a[i]-1); Add(a[i],1); } for_(i,1,m){ q[i].l=read(); q[i].r=read(); q[i].id=i; } Solve(); for_(i,1,1e5){ pos[i]=(i-1)/blo+1; if(pos[i]!=pos[i-1]) { bL[pos[i]]=i; bR[pos[i-1]]=i-1; } } bR[pos[(int)1e5]]=1e5; int sum,l,r,v,id; for_(i,1,n){ for_(j,1,pos[a[i]]-1) c[j]++; for_(j,bL[pos[a[i]]],a[i]) d[j]++; int Size=L[i].size(); for_(j,0,Size-1){ l=L[i][j].l; r=L[i][j].r; v=L[i][j].v; id=L[i][j].id; sum=0; for_(k,l,r) sum+=c[pos[a[k]+1]]+d[a[k]+1]; ans[id]+=v*sum; } } memset(c,0,sizeof(c)); memset(d,0,sizeof(d)); _for(i,n,1){ for_(j,pos[a[i]]+1,blo) c[j]++; for_(j,a[i],bR[pos[a[i]]]) d[j]++; int Size=R[i].size(); for_(j,0,Size-1){ l=R[i][j].l; r=R[i][j].r; v=R[i][j].v; id=R[i][j].id; sum=0; for_(k,l,r) sum+=c[pos[a[k]-1]]+d[a[k]-1]; ans[id]+=v*sum; } } for_(i,1,m){ ans[i]+=ans[i-1]; Ans[q[i].id]=ans[i]; } for_(i,1,m) print(Ans[i]),*o++='\n'; fwrite(O,1,o-O,stdout); } } using namespace Solve; signed main(){ #ifndef ONLINE_JUDGE fire("data"); #endif In(); } -
【点缀光辉的第十四分块(前体)】
首先分析题面,考虑对于每次进行移动,贡献是 \(\{1\sim r\}\) 内和 \(\mathbf{val}(r+1)\) 异或和中 \(1\) 的个数 减去 \(\{1\sim l-1\}\) 内和 \(\mathbf{val}(r+1)\) 异或和中 \(1\) 的个数
前面依然是预处理,后面的直接
vector存进去,和上一道题一样然后我们发现,后面的值域分块维护,解决
数组开 \(100010\),交上去,诶 \(\mathbf{WA}\) 了,调了半天发现只要改到 \(200020\) 就能过
不过这道题似乎不是很卡常,没用
Fread和Fwrite也过了,直接关同步流cin/cout点击查看代码
#define ONLINE_JUDGE #include<bits/stdc++.h> #include<sys/mman.h> #include<fcntl.h> #define N 200010 #define firein(a) freopen(a".in","r",stdin) #define fireout(a) freopen(a".out","w",stdout); #define fire(a) firein(a),fireout(a) #define for_(a,b,c) for(int a=b;a<=c;a++) #define _for(a,b,c) for(int a=b;a>=c;a--) #define For_(a,b,c,d) for(int a=b;a<=c;a+=d) #define _For(a,b,c,d) for(int a=b;a>=c;a-=d) #define lowbit(x) ((x)&(-x)) #define int long long typedef long long ll; using namespace std; namespace Solve{ // #ifndef ONLINE_JUDGE // int _if=open("data.in",O_RDONLY); // FILE* _of=fopen("data.out","w"); // #else // int _if=fileno(stdin); // FILE* _of=stdout; // #endif // const char *_I=(char*)mmap(0,1<<24,1,2,_if,0); // inline ll read(){ // int x=0; // while(*_I<48)++_I; // while(*_I>47)x=x*10+(*_I++&15); // return x; // } // char O[1<<24],*o=O; // void print(ll x){ // if (x>9)print(x/10); // *o++=x%10+48; // } int a[N],bl[N],st[N],blo,top,n,m,k; ll s1[N],s2[N],s[N],ret[N],ans[N],res; struct node{ int l,r,id; inline node(){} inline node(int L,int R,int Id):l(L),r(R),id(Id){} inline bool operator <(const node &b)const{ return bl[l]==bl[b.l]?r<b.r:l<b.l; } }q[N]; inline void Init(){ int Cnt,X; for(int i=0;i<16384;++i){ Cnt=0,X=i; for(;X;X^=lowbit(X)) ++Cnt; if(Cnt==k) st[++top]=i; } } vector<node>Q[N]; inline void Solve1(){ int l=q[1].r+1,r=q[1].r; for_(i,1,m){ if(l<q[i].l){ Q[r].push_back(node(l,q[i].l-1,q[i].id<<1)); } if(l>q[i].l){ Q[r].push_back(node(q[i].l,l-1,q[i].id<<1)); } l=q[i].l; if(r<q[i].r){ Q[l-1].push_back(node(r+1,q[i].r,q[i].id<<1|1)); } if(r>q[i].r){ Q[l-1].push_back(node(q[i].r+1,r,q[i].id<<1|1)); } r=q[i].r; } } inline void Solve2(){ int l=q[1].r+1,r=q[1].r; for_(i,1,m){ if(l<q[i].l) res-=ret[q[i].id<<1]-s2[q[i].l-1]+s2[l-1]; if(l>q[i].l) res+=ret[q[i].id<<1]-s2[l-1]+s2[q[i].l-1]; l=q[i].l; if(r<q[i].r) res+=s1[q[i].r]-s1[r]-ret[q[i].id<<1|1]; if(r>q[i].r) res-=s1[r]-s1[q[i].r]-ret[q[i].id<<1|1]; r=q[i].r; ans[q[i].id]=res; } } inline void In(){ std::ios::sync_with_stdio(false); cin.tie(nullptr);cout.tie(nullptr); cin>>n>>m>>k; blo=800; Init(); for_(i,1,n){ cin>>a[i]; bl[i]=(i-1)/blo+1; } for_(i,1,m){ cin>>q[i].l>>q[i].r; q[i].id=i; } sort(q+1,q+1+m); Solve1(); for_(i,1,n){ s1[i]=s1[i-1]+s[a[i]]; for_(k,1,top) ++s[a[i]^st[k]]; s2[i]=s2[i-1]+s[a[i]]; for(vector<node>::iterator it=Q[i].begin();it!=Q[i].end();++it) for_(k,it->l,it->r) ret[it->id]+=s[a[k]]; } Solve2(); for_(i,1,m) cout<<ans[i]<<endl; } } using namespace Solve; signed main(){ // fire("data"); In(); } -
-
题意
给定一个长度为 \(n\) 的序列 \(a\) 。给定 \(m\) 个询问,每次询问一个区间中 \([l, r]\) 中所有数的「\(\mathbf{Abbi}\) 值」之和。
\(\mathbf{Abbi}\) 值定义为:若 \(a_i\) 在询问区间 \([l, r]\) 中是第 \(k\) 小,那么它的「Abbi 值」等于 \(k \times a_i\) 。
首先看到题面,一个最为暴力的思路就出现了,莫队套上一颗平衡树,复杂度 \(\Theta(n \sqrt n \log n)\),当然块长取 \(n \log n\) 时复杂度为 \(\Theta(n \sqrt {n \log n})\),当然,我们也知道这个复杂度是过不去的
我们发现主要瓶颈在于单次移动是 \(\Theta( \log n)\) 的,凭空多了个 \(\log\) 复杂度,如果去掉这个 \(\log\) 我们就能过
因此不难想到本题需要使用二次离线莫队来维护
首先我们先将原本的拆成两部分
-
定义 \(\mathbf{Ans}(l,r,k)\) 为区间 \(\{l\sim r\}\) 比 \(a_{k}\) 小的数的个数
-
定义 \(\mathbf{Sum}(l,r,k)\) 为区间 \(\{l\sim r\}\) 比 \(a_{k}\) 大的数的和
然后对于这两个部分,我们可以把原本的式子转化为只与这两个有关的情况,这样我们就可以二次离线
向右移动一格的贡献是 \(\mathbf{Ans}(l,r,r+1)\times a_{r+1}+a_{r+1}+\mathbf{Sum}(l,r,r+1)\)
然后差分这个式子,转化成可以二次离线的形式
\((\mathbf{Ans}(1,r,r+1)-\mathbf{1,l-1,r+1})\times a_{r+1}+a_{r+1}+(\mathbf{Sum}(1,r,r+1)-\mathbf{Sum}(1,l-1,r+1))\)
熟悉的预处理,剩下一堆乱七八糟的东西扔到 \(\mathbf{vector}\) 里
考虑值域分块,然后发现是 \(n\) 次修改,\(n \sqrt n\) 次询问,所以直接增加修改的复杂度,让询问降低到 \(O(1)\)
这样我们就又一次做到了 \(\mathcal O(n \sqrt n)\) 的复杂度解决问题,可过
点击查看代码
#include<bits/stdc++.h> #include<sys/mman.h> #include<fcntl.h> typedef long long valueType; typedef std::vector< valueType > vector_with_valueType; typedef std::pair< valueType,valueType > PII; #define N 500010 #define firein(a) freopen(a".in","r",stdin) #define fireout(a) freopen(a".out","w",stdout); #define fire(a) firein(a),fireout(a) #define for_(a,b,c) for(int a=b;a<=c;a++) #define _for(a,b,c) for(int a=b;a>=c;a--) #define For_(a,b,c,d) for(int a=b;a<=c;a+=d) #define _For(a,b,c,d) for(int a=b;a>=c;a-=d) #define lowbit(x) ((x)&(-x)) #define int long long namespace Solve{ int a[N],b[N],Size,T,num,POS[N],g[N]; valueType ans[N],f[N]; struct Query{ int l,r,id,bl; inline bool operator <(const Query &b)const{ return bl!=b.bl?bl<b.bl:bl&1?r<b.r:r>b.r; } }Q[N]; struct Query_In_vector{ int l,r,id; Query_In_vector(int l=0,int r=0,int id=0): l(l),r(r),id(id){} }; std::vector<Query_In_vector> vec[N<<1]; int belong[N]; class block{ public: int l,r; }bl[N]; int bl_Cnt[N],Cnt[N],Sum[N],bl_Sum[N]; inline void Init(){ Size=800,T=num/Size; for_(i,1,T){ bl[i].l=(i-1)*Size+1; bl[i].r=i*Size; } if(bl[T].r<num){ bl[T+1].l=bl[T].r+1; bl[T+1].r=num; T++; } for_(i,1,num){ belong[i]=(i-1)/Size+1; } } inline void Insert(int x,int val){ int Belong=belong[x]; for_(i,x,bl[Belong].r){ ++Cnt[i]; Sum[i]+=val; } for_(i,Belong+1,T){ ++bl_Cnt[i]; bl_Sum[i]+=val; } } inline void Clear(){ for_(i,1,num) Cnt[i]=Sum[i]=0; for_(i,1,T) bl_Cnt[i]=bl_Sum[i]=0; } inline int The_First_Query(int left,int right){ return (bl_Cnt[belong[right]]+Cnt[right])-(bl_Cnt[belong[left-1]]+Cnt[left-1]); } inline int The_Second_Query(int left,int right){ return (bl_Sum[belong[right]]+Sum[right])-(bl_Sum[belong[left-1]]+Sum[left-1]); } #define SUM1(left,right) The_First_Query(left,right) #define SUM2(left,right) The_Second_Query(left,right) inline void Sort_Pre(int n,int m){ std::sort(Q+1,Q+1+m); int l=1,r=0; for_(i,1,m){ if(l<Q[i].l){ vec[r].push_back(Query_In_vector{l,Q[i].l-1,-Q[i].id}); ans[Q[i].id]+=g[Q[i].l-1]-g[l-1]; l=Q[i].l; } if(l>Q[i].l){ vec[r].push_back(Query_In_vector{Q[i].l,l-1,Q[i].id}); ans[Q[i].id]-=g[l-1]-g[Q[i].l-1]; l=Q[i].l; } if(r<Q[i].r){ vec[l-1].push_back(Query_In_vector{r+1,Q[i].r,-Q[i].id}); ans[Q[i].id]+=f[Q[i].r]-f[r]; r=Q[i].r; } if(r>Q[i].r){ vec[l-1].push_back(Query_In_vector{Q[i].r+1,r,Q[i].id}); ans[Q[i].id]-=f[r]-f[Q[i].r]; r=Q[i].r; } } } inline void Solve_The_Problem(int n,int m){ Clear(); for_(i,1,n){ Insert(a[i],b[a[i]]); for(auto x:vec[i]){ for_(j,x.l,x.r){ valueType res=SUM1(1,a[j]-1)*b[a[j]]+SUM2(a[j]+1,num); if(x.id>0) ans[x.id]+=res; else ans[-x.id]-=res; } } } } inline void In(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr); int n,m; std::cin >> n >> m; for_(i,1,n){ std::cin >> a[i]; b[i] = a[i]; } std::sort(b+1,b+1+n); num=std::unique(b+1,b+1+n)-(b+1); for_(i,1,n){ a[i]=std::lower_bound(b+1,b+num+1,a[i])-b; } Init(); for_(i,1,n){ Insert(a[i],b[a[i]]); int res=SUM1(1,a[i]-1)*b[a[i]]+SUM2(a[i]+1,num); f[i]=f[i-1]+res+b[a[i]]; g[i]=g[i-1]+res-b[a[i]]; } int SIZE=n/sqrt(m*2/3); for_(i,1,n){ POS[i]=(i-1)/SIZE+1; } for_(i,1,m){ std::cin >> Q[i].l >> Q[i].r; Q[i].id=i; Q[i].bl=POS[Q[i].l]; } Sort_Pre(n,m); Solve_The_Problem(n,m); for_(i,1,m){ ans[Q[i].id]+=ans[Q[i-1].id]; } for_(i,1,m){ std::cout << ans[i] << '\n'; } } } using namespace Solve; signed main(){ #ifndef ONLINE_JUDGE fire("data"); #endif In(); } -
回滚莫队
我们在写莫队的时候,可以发现有的时候删除操作或者增加操作内有一种非常难以实现或者复杂度巨大
因此回滚莫队就诞生了
回滚莫队的核心思想就是:只实现一个操作,剩下的交给回滚来解决
回滚莫队又可以分为只使用增加操作的莫队和只使用删除操作的莫队
只加不减
我们可以考虑一个区间问题,在问题中加点可以很轻易的转移而删点不能,我们就可以使用以下算法
-
首先对询问进行分块,排序,左端点所在的块升序为第一关键字,右端点升序为第二关键字
-
对于处理左端点在块 \(\mathbf T\) 内的询问,我们先初始化左端点为 \({right(\mathbf T)} + 1\),右端点初始化为 \(right(\mathbf T)\)
-
对于左右端点在一个块内的询问,我们直接扫描求解即可
-
对于左右端点不在一个块内的询问,如果询问的右端点大于莫队区间的右端点,那么不断扩展右端点直至莫队区间的右端点等于询问的右端点
-
接下来不断扩展莫队区间的左端点直至莫队区间的左端点等于询问的左端点
-
回答询问,撤销莫队区间左端点的改动,让左端点回到 \({right(\mathbf T)}+1\) 的位置,继续回答询问
复杂度证明
对于左右端点在一个块内的询问,复杂度很明显是 \(\mathcal {O}(n \times \mathrm{SIZE})\),其中 \(\mathrm{SIZE}\) 是块长
对于不在一个块内的询问,因为它们的右端点是单调递增的,移动右端点的复杂度是 \(\mathcal {O}(n)\) 的,移动左端点单次不会超过 \(\mathrm{SIZE}\) 因为有 \(\frac{n}{\mathrm{SIZE}}\) 个块
所以总复杂度是 \(\mathcal O(m \times \mathrm{SIZE} + \frac{n^2}{\mathrm{SIZE}})\),当 \(\mathrm{SIZE}\) 取 \(b=\sqrt{n}\) 最优(假设 \(n\),\(m\) 同阶),此时复杂度为 \(\mathcal O(n \sqrt n)\)
只减不加
算法类似只加不减的回滚莫队,只是有略微的差距
-
首先对询问进行分块,排序,左端点所在的块升序为第一关键字,右端点升序为第二关键字
-
对于处理左端点在块 \(\mathbf T\) 内的询问,我们先初始化左端点为 \({left(\mathbf T)}\),右端点初始化为 \(n\)
-
对于左右端点在一个块内的询问,我们直接扫描求解即可
-
对于左右端点不在一个块内的询问,由于其右端点降序,从 \(n\) 的位置开始,我们对右端点只做删点操作,总共最多删点 \(n\) 次
-
接下来不断删除莫队区间的左端点直到区间的左端点等于询问的左端点
-
回答询问,撤销改动,继续回答
复杂度证明
同 "只加不减" 莫队的证明
例题
-
本题是回滚莫队的板子
观察题目发现加法很简单,减法则较难实现
考虑使用回滚莫队,每次进行扩展操作时维护区间的每一个值的最左端和最右端,暴力维护即可
点击查看代码
#include<bits/stdc++.h> #include<sys/mman.h> #include<fcntl.h> typedef long long valueType; typedef std::vector< valueType > vector_with_valueType; typedef std::pair< valueType,valueType > PII; #define N 500010 #define firein(a) freopen(a".in","r",stdin) #define fireout(a) freopen(a".out","w",stdout); #define fire(a) firein(a),fireout(a) #define for_(a,b,c) for(int a=b;a<=c;a++) #define _for(a,b,c) for(int a=b;a>=c;a--) #define For_(a,b,c,d) for(int a=b;a<=c;a+=d) #define _For(a,b,c,d) for(int a=b;a>=c;a-=d) #define lowbit(x) ((x)&(-x)) #define int long long namespace Solve{ int X[N],POS[N],Size,tot,Left[N],Right[N],Cnt,last[N],b[N],ans[N],clear[N],blo; class Query{ public: int l,r,id; inline bool operator < (const Query &B)const{ if (POS[l] == POS[B.l]) return r < B.r; return POS[l] < POS[B.l]; } }Q[N]; inline int Calc(int l,int r){ int res=0; for(int i=l;i<=r;i++) last[X[i]]=0; for(int i=l;i<=r;i++) if(last[X[i]]) res=std::max(res,i-last[X[i]]); else last[X[i]]=i; return res; } int Y[N]; inline void In(){ int n,m; std::cin >> n; Size=sqrt(n); for_(i,1,n){ std::cin >> X[i]; b[i]=X[i]; POS[i]=(i-1)/Size+1; } blo=POS[n]; std::sort(b+1,b+n+1); int num=std::unique(b+1,b+n+1)-(b+1); for_(i,1,n) X[i]=std::lower_bound(b+1,b+num+1,X[i])-b; std::cin >> m; for_(i,1,m){ std::cin >> Q[i].l >> Q[i].r; Q[i].id=i; } std::sort(Q+1,Q+m+1); int i=1; for_(j,1,blo){ int right=std::min(j*Size,n),l=right+1,r=right,now=0,Cnt=0; for(;POS[Q[i].l]==j;i++){ if(POS[Q[i].r]==j){ ans[Q[i].id]=Calc(Q[i].l,Q[i].r); continue; } while(r<Q[i].r){ r++; Right[X[r]]=r; if(!Left[X[r]]) Left[X[r]]=r,clear[++Cnt]=X[r]; now=std::max(now,r-Left[X[r]]); } int tmp=now; while(l>Q[i].l){ l--; if(!Right[X[l]]) Right[X[l]]=l; now=std::max(now,Right[X[l]]-l); } ans[Q[i].id]=now; while(l<=right){ if(Right[X[l]]==l) Right[X[l]]=0; l++; } now=tmp; } for_(k,1,Cnt) Left[clear[k]]=Right[clear[k]]=0; } for_(i,1,m) std::cout << ans[i] << "\n"; } } using namespace Solve; signed main(){ #ifndef ONLINE_JUDGE fire("data"); #endif In(); } -
我们发现对于这道题,减法是非常难以实现的
所以考虑使用回滚莫队,每次进行一次扩展操作的贡献只要按照题意模拟即可
点击查看代码
#include<bits/stdc++.h> #include<sys/mman.h> #include<fcntl.h> typedef long long valueType; typedef std::vector< valueType > vector_with_valueType; typedef std::pair< valueType,valueType > PII; #define N 500010 #define firein(a) freopen(a".in","r",stdin) #define fireout(a) freopen(a".out","w",stdout); #define fire(a) firein(a),fireout(a) #define for_(a,b,c) for(int a=b;a<=c;a++) #define _for(a,b,c) for(int a=b;a>=c;a--) #define For_(a,b,c,d) for(int a=b;a<=c;a+=d) #define _For(a,b,c,d) for(int a=b;a>=c;a-=d) #define lowbit(x) ((x)&(-x)) #define int long long namespace Solve{ int X[N],POS[N],Size,Dis[N],tot; int Cnt[N],ans[N],cnt[N]; class block{ public: int l,r; }bl[N]; class The_Query{ public: int l,r,id; }Q[N]; inline bool The_Cmp_for_Query(The_Query A,The_Query B){ if (POS[A.l] == POS[B.l]) return A.r < B.r; return POS[A.l] < POS[B.l]; } inline void build(int n,int m){ Size=800; tot=n/Size; for_(i,1,tot){ bl[i].l=(i-1)*Size+1; bl[i].r=i*Size; } if(bl[tot].r<n){ bl[tot+1].l=bl[tot].r+1; bl[tot].r=n; ++tot; } for_(i,1,tot){ for_(j,bl[i].l,bl[i].r){ POS[j]=i; } } } inline void Add(int v,int &Ans){ ++cnt[v]; Ans=std::max(Ans,cnt[v]*Dis[v]); } inline void Del(int v){ --cnt[v]; } inline void Sort(int n,int m){ int l=1,r=0,left,right,the_last_block=0; valueType The_Ans=0,tmp=0; for_(i,1,m){ if(POS[Q[i].l]==POS[Q[i].r]){ for_(j,Q[i].l,Q[i].r) ++Cnt[X[j]]; for_(j,Q[i].l,Q[i].r) ans[Q[i].id]=std::max(ans[Q[i].id],Dis[X[j]]*Cnt[X[j]]); for_(j,Q[i].l,Q[i].r) --Cnt[X[j]]; continue; } if(POS[Q[i].l]!=the_last_block) { while(r>bl[POS[Q[i].l]].r){ Del(X[r]); --r; } while(l<bl[POS[Q[i].l]].r+1){ Del(X[l]); ++l; } The_Ans=0; the_last_block=POS[Q[i].l]; } while(r<Q[i].r){ ++r; Add(X[r],The_Ans); } left=l; tmp=The_Ans; while(left>Q[i].l){ --left; Add(X[left],tmp); } ans[Q[i].id]=tmp; while(left<l){ Del(X[left]); ++left; } } } inline void In(){ std::ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr); int n,m; std::cin >> n >> m; for_(i,1,n){ std::cin >> X[i]; Dis[i]=X[i]; } for_(i,1,m){ std::cin >> Q[i].l >> Q[i].r; Q[i].id=i; } build(n,m); std::sort(Q+1,Q+1+m,The_Cmp_for_Query); std::sort(Dis+1,Dis+1+n); int num=std::unique(Dis+1,Dis+1+n)-(Dis+1); for_(i,1,n){ X[i]=std::lower_bound(Dis+1,Dis+1+num,X[i])-(Dis); } Sort(n,m); for_(i,1,m){ std::cout << ans[i] << "\n"; } } } using namespace Solve; signed main(){ #ifndef ONLINE_JUDGE fire("data"); #endif In(); } -
【沉滞留驻的第十一分块】

