【学习笔记】 字符串基础 : 后缀自动机(基础篇)
本文只介绍关于 的基本概念与实现
后缀自动机是什么
类似 自动机,后缀自动机() 是能且只能接收字符串所有后缀的自动机
我们首先要知道, 是只能接收所有后缀的结构而不是只能维护后缀的结构
事实上 的主要作用是维护字符串 的每一个子串(因为一个 的子串一定是一个 的后缀的前缀)
在下文中我们将定义 为字符集, 为字符集大小
后缀自动机的定义
是一张 ,节点被称作状态,边被称作转移
图中存在一个源点 称作初始节点,其他所有节点均可从 到达
每个边都标有一些字符,从一个节点出发的所有边都不同(也就是说没有相同的字母作为边)
存在至少一个终止的状态,从 出发最后转移到一个终止状态,那么路径上所有边链接起来一定是字符串 的一个后缀,每个字符串 的后缀都可以用一个 到某个终止状态的路径来构成
下文中我们定义以下内容
-
代表一个串的结束位置

这样我们可以把子串根据 分为若干种的等价类
我们可以得到几个重要引理(钦定 )
-
当字符串 在 中的每次出现,都是以 后缀的形式存在时,字符串 的两个非空子串 和 的 相同
证明:
-
若 和 的 相同,则 是 的一个只以 中的一个 的后缀的形式出现后缀
-
若 为 的一个后缀且在 中出现时只以后缀的形式,两个子串的 相同。
因此得证
-
-
和 的 集合要么不交,要么完全包含
两者关系为
证明:
-
在 是 的后缀时,类似上图内的 “能够接收 的串的节点一定可以接受 ”
-
若集合 与 有至少一个公共元素,那么由于字符串 与 在相同位置结束, 是 的一个后缀。
-
所以在每次 出现的位置,子串 也会出现。所以
因此得证
-
-
将一个 等价类中的所有子串按长度非递增的顺序进行排序
每个子串长度都小于等于它前一个子串且每个子串是它前一个子串的后缀
因此对于同一等价类的任一两子串,较短者为较长者的后缀且类中的子串长度恰好覆盖整个区间 。
-
-
代表一个节点能控制的最大长度,比如当一个节点可以控制 和 时其控制的最大长度( )也就是 代表的
-
一个节点其连接的 节点是其的一个后缀,因为节点是按照 来分的,所以其的 是其后缀内 集合不同的最长的后缀
后缀自动机的构建过程
假设要建立的串是 ,我们先建立一条链

然后加入一些边来维护后缀自动机,让后缀自动机能够记录所有的后缀
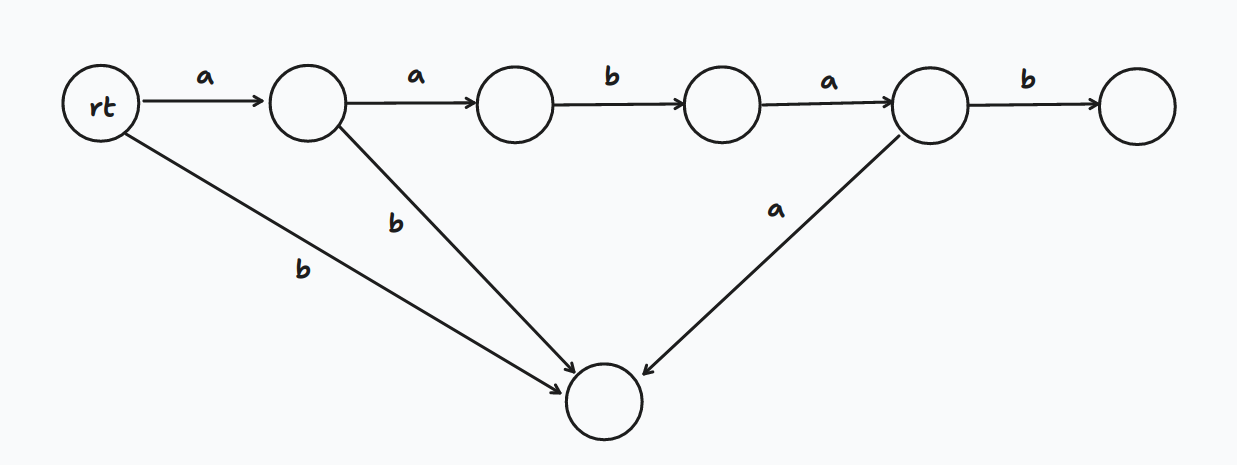
再比如说要建立的串是 ,那么建立出的后缀自动机形态为
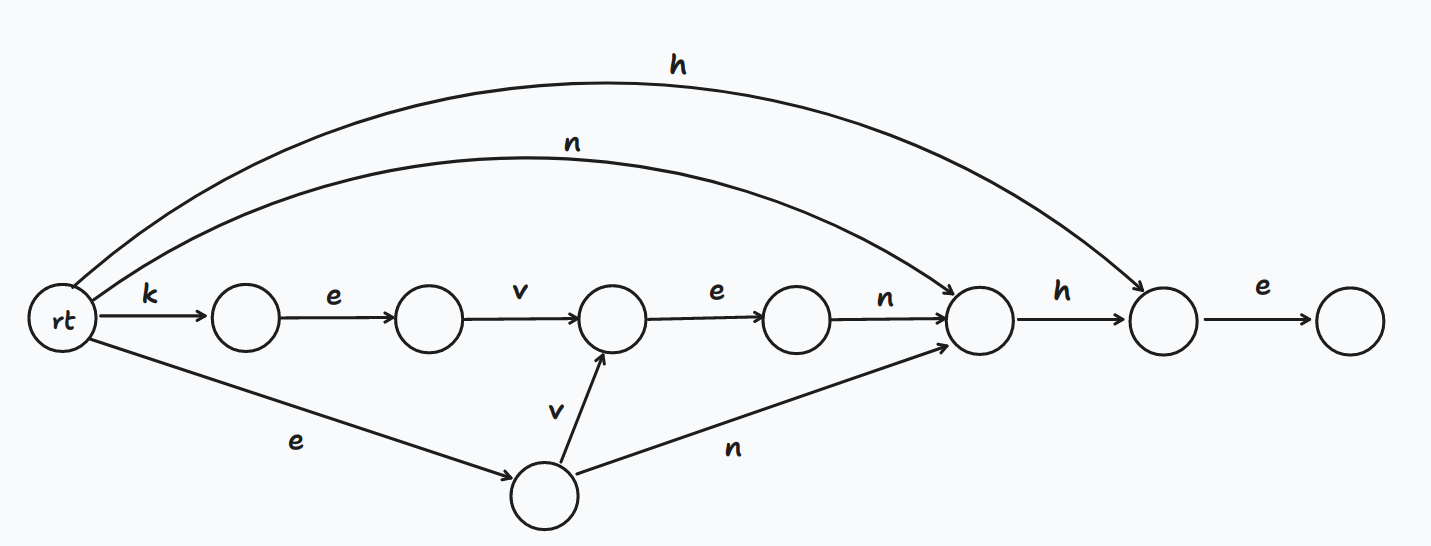
我们发现,在第一个建立完毕的 内存在多个 串,而如果我们查询 串就只能查询到第一个出现的 串(也就是先向右再向下)
因此我们需要引入一个名为 树的数据结构来统计本质相同的子串
树的建立
后缀链接
对于 树,我们需要一个名为 (后缀链接)的东西来维护
定义
考虑 中某个不是 的状态 , 对应于具有相同 的等价类。
定义 为这些字符串中最长的一个,则所有其它的字符串都是 的后缀。
同时,字符串 的前几个后缀(按长度降序考虑)全部包含于这个等价类,且所有其它后缀在其它的等价类中。
记最长的这样的后缀为 ,将 的后缀链接连到 上
一个 后缀链接 连接到对应于 的最长后缀的另一个 等价类的状态
通过 建立的树和通过 建立的树形态是相同的
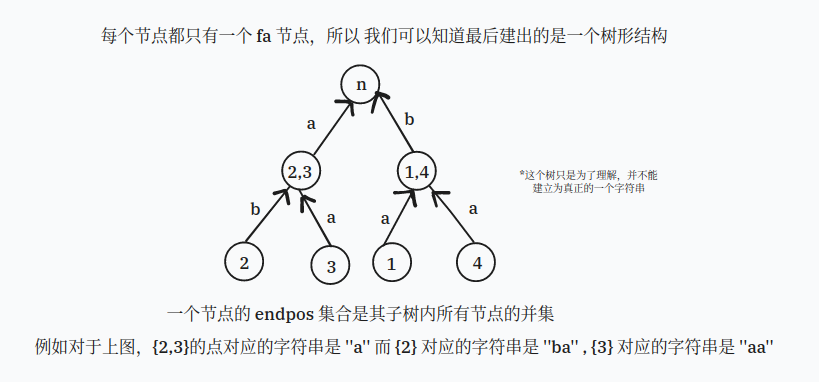
如上图
其中这些链接这些节点的边其实和后缀链接 本质相同
我们可以发现最后建立的一定是一颗树的形状,其中根节点一定是
这棵树就是我们的 树了
定理
-
设一个 等价类为 , 中最短的串为 。
那么 (这里因为如果相等会合并为一个 所以不能取等)
-
中最长的串是 的长度为 的真后缀。
的建造
我们把 树和最开始建出的 放到一起就形成了
下面的是以 为例建出的 了
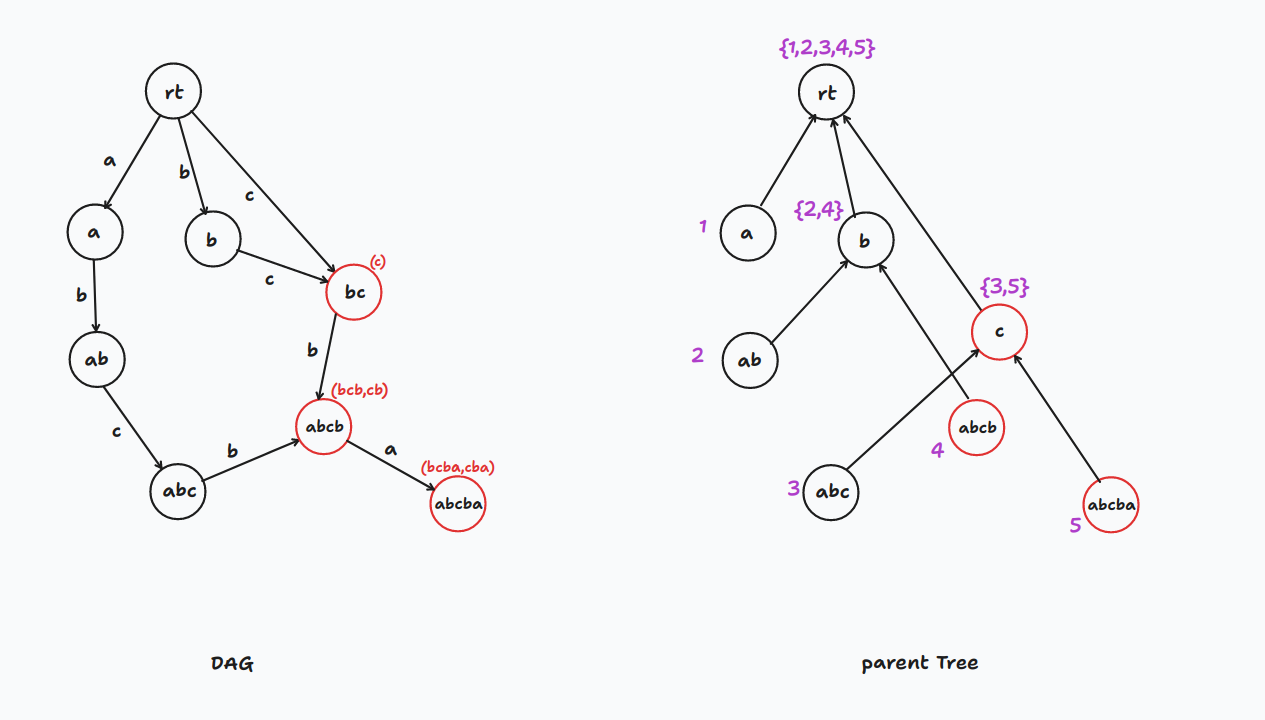
树与 公用结点,但二者的边都是独有的
构造算法
下面的是 的算法流程
初始化:,
-
令 为添加字符 之前整个字符串 所对应的结点(从 出发走到 的路径上边组成的字符串就是 ,初始 )。
-
创建一个新的状态 ,让
-
从 开始对 进行遍历,若当前结点 没有 的边,创建一条 的边并标记为
-
若遍历到了 则让 , ,回到第一步
-
如果当前结点 已经有了标记字符 的出边则停止遍历,并把这个结点标记为 ,标记 沿着标记字符 的出边到达的点为 。
-
如果 ,让 ,回到第一步。
-
复制状态 到一个新的状态 里(包括 以及所有 在 上的出边),将 赋值为 。
复制之后,再赋值
然后从 遍历后缀链接,设当前遍历到的点为 ,若 有标记为 的出边 ,则重定向这条边为
若 没有标记为 的出边或者 的标记为 的出边所到达的点不是 ,停止遍历, ,回到第一步
我们一步一步的来看这个算法
-
找到 来为后面的更新做准备
-
加入 后,我们会形成一个新的等价类(因为 包含了新字符 的位置),我们定义这个新的等价类为
根据对 的定义,我们可以发现 内最长的字符串一定是 ,所以
我们知道,新加入的字符是 ,所以新串是 ,我们需要链接一条从 到 的边,标记为 表示可以从 转移到
那么等价类 内的最长字符串一定是 ,长度显然为
-
遍历 并尝试加入关于 的转移,我们知道 是记录的所有后缀,我们只要在后面加入一个
我们知道,从 开始跳 可以跳到所有后缀,只要依次在这些等价类内向 试图加入标记为 的转移即可
然而我们只能添加与原有转移不冲突的转移。因此我们只要找到已存在的 的转移,我们就必须停止
下面的图片是对于字符串 加入一个新的字符 后的结果
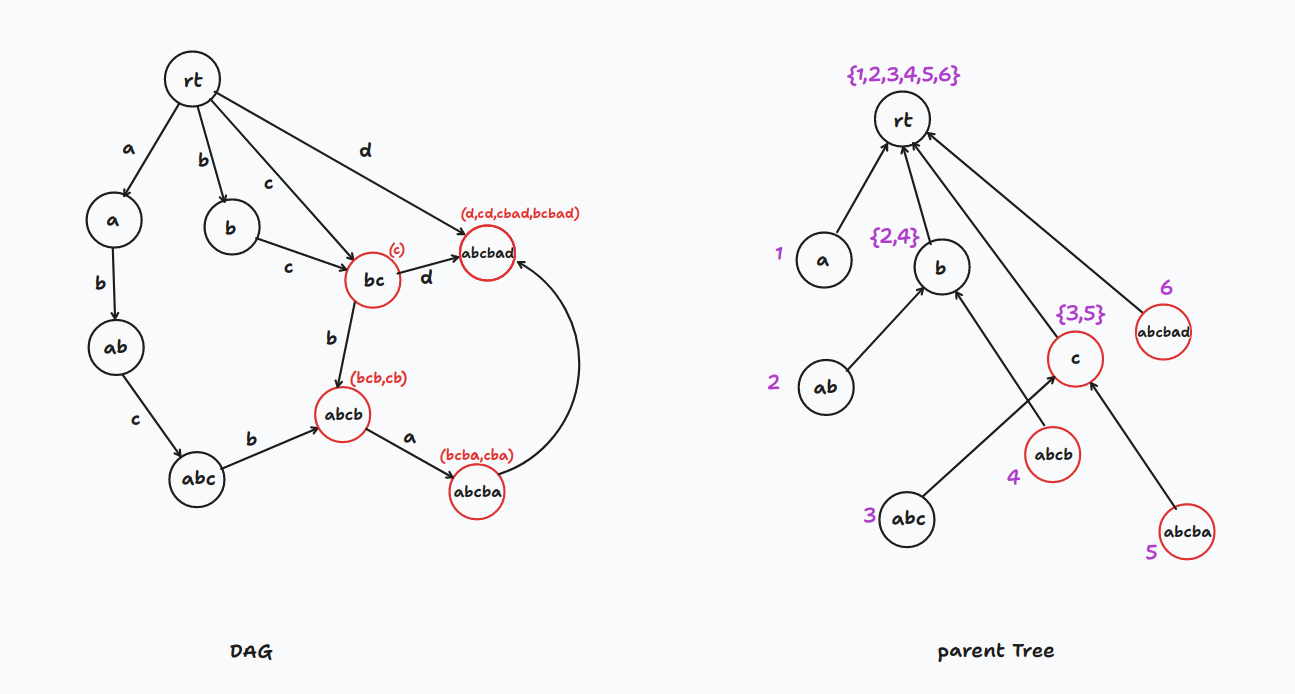
我们发现当从 一直跳 跳到了 节点,那么证明 内没有出现过 节点
-
我们到达了虚拟状态 ,这意味着我们为所有 的后缀添加了 的转移。这也意味着,字符 从未在字符串 中出现过。
因此 的后缀链接为状态
-
第二种情况,我们找到了 的状态转移,说明我们正在试图添加一个已经存在的 (为当前这个节点代表的 的后缀)
我们似乎不应该在这里加入一个标记为 的转移,所以我们应该把 连到一个 为 的状态上
-
如果 ,也就是说转移 是连续的
我们只需要让 连到 即可
-
如果 ,也就是转移 并非连续
那么这意味着状态 不只对应于长度为 的后缀 ,还对应于 的更长的子串
我们就被迫只能把 一分为二了,让第一个状态 的 为
首先我们对于 复制一个状态 ,让 ,然后把 的所有转移复制到 上
同时,我们把 的目标也设为 的目标,并且让 的目标设定为
接下来我们重定向一些边(因为分开之后我们必须要区分清哪些入边构成了被分出去的 ,哪些构成了还剩下在 中的串),然后继续遍历 并且分类讨论
-
找到了一个结点 拥有一条标记 的出边指向
说明 中的串加上 构成了 中的串,我们要把这条边重定向到 。
-
找到了一个结点 拥有一条标记 的出边,但指向结点不是
说明 中的串加上 构成了一个不在 集合中的 内最长串的后缀( 在 树上的某一级祖先中的一个串)。
因为 中的串加上 无法构成 中的串,则 的后缀加上 显然也无法构成 中的一个串。
也就是说,我们已经把所有要重定向的边完成重定向了,停止遍历即可。
-
关于 线性复杂度的证明
的复杂度是线性的必要前提是 为常数
在使用 map 的情况下时间复杂度为 ,空间复杂度为
在不使用 map 的情况下时间复杂度 , 空间复杂度为
警惕 SAM 题目常见卡 unordered_map 的坏人
我们认为字符集的大小为常数,即每次对一个字符搜索转移、添加转移、查找下一个转移的时间复杂度都为
在算法中有三处不是明显线性的,我们一一来分析
-
遍历所有状态 的后缀链接,添加字符 的转移。
对于后缀自动机大小,很明显转移数和状态数是线性的,所以这里一定是线性的
-
当状态 被复制到一个新的状态 时复制转移的过程
同上一条,后缀自动机的转移数和状态数很明显是线性的,所以是线性的
-
第三处是修改指向 的转移,将它们重定向到 的过程。
结论: 的位置单调递增,所以这个循环最多不会执行超过 次迭代
证明:
-
将最初指向 的转移重定向到 ,记 ,这是一个字符串 的后缀,每次迭代长度都递减(字符串 的位置每次迭代都单调上升)。
-
这种情况下,如果在循环的第一次迭代之前,相对应的字符串 在距离 的深度为 的位置上(深度记为后缀链接的数量)
-
那么在最后一次迭代后,字符串 将会成为路径上第二个从 出发的后缀链接(它会成为新的 的值)
-
所以 的位置单调递增
-
实现
下面是基于 map 实现的 SAM,复杂度为
当 SAM 跑的不应为字符串即为数字时改变 valueType 即可
点击查看代码
#include<bits/stdc++.h>
typedef char valueType;
namespace Suffix_AutoMaton{
#define for_(a,b,ch) for(int a=b;a<=ch;a++)
#define _for(a,b,ch) for(int a=b;a>=ch;a--)
constexpr int MaxLen=1e5+5;
class SAM{
public:
int len, Link;
std::map<valueType,int> Next;
}sam[MaxLen<<1];
int Size,Last;
inline void Init() {
sam[0].len=0;
sam[0].Link=-1;
Size++;Last=0;
}
inline void Insert(valueType ch) {
int cur=Size++,p=Last;
sam[cur].len=sam[Last].len+1;
while((p!=-1)&&(
!sam[p].Next.count(ch))){
sam[p].Next[ch]=cur;
p=sam[p].Link;
}
if(p==-1)
sam[cur].Link=0;
else {
int q=sam[p].Next[ch];
if(sam[p].len+1==sam[q].len)
sam[cur].Link=q;
else{
int E=Size++;
sam[E].len=sam[p].len+1;
sam[E].Next=sam[q].Next;
sam[E].Link=sam[q].Link;
while(p!=-1&&sam[p].Next[ch]==q){
sam[p].Next[ch]=E;
p=sam[p].Link;
}
sam[q].Link=sam[cur].Link=E;
}
}
}
#undef for_
#undef _for
}using namespace Suffix_AutoMaton;
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
}
性质
-
对于字符串 ,它的 中的状态数 不会超过
证明:
-
算法本身就可以证明,首先一开始我们会自带状态,然后第一轮和第二轮最多只会创建 个状态
后面的每轮最多只会创建 个状态,所以不会超过
-
-
对于字符串 ,它的 中的转移数 不会超过
-
分配结束标记
我们知道, 是一个能接收所有后缀的最小的 ,因此我们要分配结束标记
先构建完整颗 ,这样找到构建完毕后的 ,然后从 往根节点跳,路上的所有节点全部打一个结束标记就行了
应用
详见【学习笔记】 - 字符串基础 : 后缀自动机(进阶篇)
例题
详见【学习笔记】 - 字符串基础 : 后缀自动机(进阶篇)



