【做题纪要】4月“祝祷转过千年诗篇”- 『雪山之眼』
(做题纪要前放点闲话应该没啥问题...吧?)
禾念你虽然pv里的藏文格式全都错了但是应该不至于直接把藏文全删了吧(
还有天依游学记怎么这么快就还剩十几天就要完结了，哭哭
P2408 不同子串个数
板子题，最后结果为 \(\dfrac{n(n+1)}{2}-\sum\limits_{i=2}^{n}\text h_i\)
这个我应该在学习笔记里写了，这里挂一下
代码
点击查看代码
namespace solve{
int height[N],sa[N],oldsa[N],rk[N],oldrk[N],cnt[N],key[N];
namespace SA{
inline bool cmp(int x,int y,int w){
return (oldrk[x]==oldrk[y])&&(oldrk[x+w]==oldrk[y+w]);
}
inline void Init(char *s){
int n=strlen(s+1),m=127,tot;
for_(i,1,n)
rk[i]=s[i],
++cnt[rk[i]];
for_(i,1,m)
cnt[i]+=cnt[i-1];
_for(i,n,1) sa[cnt[rk[i]]--]=i;
for(int w=1;;w<<=1,m=tot) {
tot=0;
_for(i,n,n-w+1)
oldsa[++tot]=i;
for_(i,1,n)
if(sa[i]>w)
oldsa[++tot]=sa[i]-w;
memset(cnt,0,sizeof(cnt));
for_(i,1,n)
++cnt[key[i]=rk[oldsa[i]]];
for_(i,1,m)
cnt[i]+=cnt[i-1];
_for(i,n,1)
sa[cnt[key[i]]--]=oldsa[i];
memcpy(oldrk+1,rk+1,n*sizeof(int));
tot=0;
for_(i,1,n)
rk[sa[i]]=((cmp(sa[i],sa[i-1],w))?(tot):(++tot));
if(tot==n)
break;
}
}
inline void Init_H(char *s){
int n=strlen(s+1),tot=0;
for_(i,1,n){
if(!rk[i]) continue;
if(tot) --tot;
while(s[i+tot]==s[sa[rk[i]-1]+tot]) ++tot;
height[rk[i]]=tot;
}
}
}
using namespace SA;
inline void In(){
int n,ans=0;
char s[N];
FastI>>n>>(s+1);
Init(s);Init_H(s);
for_(i,2,n) ans+=height[i];
FastO<<((n*(n+1)/2)-ans)<<endl;
}
}
using namespace solve;
P3181 「HAOI2016」找相同字符
大到小扫描 \(\text {height}\) 数组，合并相邻后缀
当前块中的贡献就是第一个串的后缀数 $\times $ 第二个串的后缀数 \(\times\) 当前枚举的 \(\text {height}\)。
因此我们直接用并查集维护即可
代码
点击查看代码
namespace solve{
int height[N],sa[N],oldsa[N],rk[N],oldrk[N],cnt[N],key[N];
namespace SA{
inline bool cmp(int x,int y,int w){
return (oldrk[x]==oldrk[y])&&(oldrk[x+w]==oldrk[y+w]);
}
inline void Init(char *s){
int n=strlen(s+1),m=127,tot;
for_(i,1,n)
rk[i]=s[i],
++cnt[rk[i]];
for_(i,1,m)
cnt[i]+=cnt[i-1];
_for(i,n,1) sa[cnt[rk[i]]--]=i;
for(int w=1;;w<<=1,m=tot) {
tot=0;
_for(i,n,n-w+1)
oldsa[++tot]=i;
for_(i,1,n)
if(sa[i]>w)
oldsa[++tot]=sa[i]-w;
memset(cnt,0,sizeof(cnt));
for_(i,1,n)
++cnt[key[i]=rk[oldsa[i]]];
for_(i,1,m)
cnt[i]+=cnt[i-1];
_for(i,n,1)
sa[cnt[key[i]]--]=oldsa[i];
memcpy(oldrk+1,rk+1,n*sizeof(int));
tot=0;
for_(i,1,n)
rk[sa[i]]=((cmp(sa[i],sa[i-1],w))?(tot):(++tot));
if(tot==n)
break;
}
}
inline void Init_H(char *s){
int n=strlen(s+1),tot=0;
for_(i,1,n){
if(!rk[i]) continue;
if(tot) --tot;
while(s[i+tot]==s[sa[rk[i]-1]+tot]) ++tot;
height[rk[i]]=tot;
}
}
}
using namespace SA;
int f[N],g[N],A[N],B[N];
inline bool cmp1(int a,int b){
return height[a]>height[b];
}
inline int find(int x){
return f[x]=((f[x]!=x)?find(f[x]):x);
}
char s1[N],s2[N],s[N];
inline void In(){
FastI>>(s1+1)>>(s2+1);
int len1=strlen(s1+1);
int len2=strlen(s2+1);
int n=len1+len2+1;
for_(i,1,n){
if(i==len1+1) s[i]='#';
else if(i<=len1) s[i]=s1[i];
else s[i]=s2[i-len1-1];
}
Init(s);Init_H(s);
for_(i,1,n){
g[i]=i+1;f[i]=i;
if(sa[i]>len1+1) B[i]=1;
if(sa[i]<=len1) A[i]=1;
}
sort(g+1,g+1+n,cmp1);
int ans=0;
for_(i,1,n-1){
int x=find(g[i]),y=find(g[i]-1);
ans+=(A[x]*B[y]+A[y]*B[x])*height[g[i]];
A[y]+=A[x];B[y]+=B[x];
f[x]=y;
}
write(ans);
}
}
P4070「SDOI2016」生成魔咒
题意
在一个字符串后加上字符，问加上这个字符后有多少本质不同的字符串
思路
首先看到不同的字符串可以很容易的想到本题需要使用 \(\text{SA}\)
正着做不好写，所以离线，把插入字符串换成删除字符串，直接求出最后全部加入完情况下的 \(\text {height}\) 数组
静态求本质不同的字符串很好求，上面第一道题就是，结果为 \(\large \frac{n(n+1)}{2}\)
这样我们贡献就好维护了，对于删除一个位置为 \(i\) 的字符，我们定义其前一个存在的和后一个存在的后缀字符串为 last 和 nxt
结果很明显是 \(ans+ \text{LCP}(last,rk[i]) + \text{LCP}(rk[i],nxt) - \text {LCP}(last,nxt)\)
随便挂个类似 set 的东西来维护就行
代码
警钟长鸣，char数组直接存巨大数字会溢出
点击查看代码
namespace solve{
int height[N],sa[N],oldsa[N],rk[N],oldrk[N];
ll cnt[N],key[N];
namespace SA{
inline bool cmp(ll x,ll y,ll w){
return (oldrk[x]==oldrk[y])&&(oldrk[x+w]==oldrk[y+w]);
}
inline void Init(int *s,int n){
int m=127000,tot;
for_(i,1,n)
rk[i]=s[i],
++cnt[rk[i]];
for_(i,1,m)
cnt[i]+=cnt[i-1];
_for(i,n,1) sa[cnt[rk[i]]--]=i;
for(ll w=1;;w<<=1,m=tot) {
tot=0;
_for(i,n,n-w+1)
oldsa[++tot]=i;
for_(i,1,n)
if(sa[i]>w)
oldsa[++tot]=sa[i]-w;
memset(cnt,0,sizeof(cnt));
for_(i,1,n)
++cnt[key[i]=rk[oldsa[i]]];
for_(i,1,m)
cnt[i]+=cnt[i-1];
_for(i,n,1)
sa[cnt[key[i]]--]=oldsa[i];
memcpy(oldrk+1,rk+1,n*sizeof(int));
tot=0;
for_(i,1,n)
rk[sa[i]]=((cmp(sa[i],sa[i-1],w))?(tot):(++tot));
if(tot==n)
break;
}
}
inline void Init_H(int *s,int n){
int tot=0;
for_(i,1,n){
if(!rk[i]) continue;
if(tot) --tot;
while(s[i+tot]==s[sa[rk[i]-1]+tot]) ++tot;
height[rk[i]]=tot;
}
}
}
using namespace SA;
ll val[N],a[N],san[N];char s[N];
namespace STree{
class Tree{
public:
int maxm,minm,lazy,l,r;
}T[N];
inline void build(int q,int l,int r){
T[q].l=l;T[q].r=r;
if(l==r) {
T[q].maxm=T[q].minm=val[l];
}
build(lc(q),l,mid(l,r));
build(rc(q),mid(l,r)+1,r);
T[q].maxm=max(T[lc(q)].maxm,T[rc(q)].maxm);
T[q].minm=min(T[lc(q)].minm,T[rc(q)].minm);
}
inline void lazy(int q){
if(T[q].lazy){
T[lc(q)].lazy+=T[q].lazy;
T[rc(q)].lazy+=T[q].lazy;
T[lc(q)].minm+=T[q].lazy;
T[rc(q)].minm+=T[q].lazy;
T[lc(q)].maxm+=T[q].lazy;
T[rc(q)].maxm+=T[q].lazy;
T[q].lazy=0;
}
}
inline void change(int q,int l,int r,int val){
if(T[q].l>r || T[q].r<l) return;
if(T[q].lazy) lazy(q);
if(T[q].l>=l && r<=T[q].r){
T[q].maxm+=val;
T[q].minm+=val;
}
change(lc(q),l,r,val);
change(rc(q),l,r,val);
T[q].maxm=max(T[lc(q)].maxm,T[rc(q)].maxm);
T[q].minm=min(T[lc(q)].minm,T[rc(q)].minm);
}
inline int Askmin(int q,int l,int r){
if(T[q].l>r || T[q].r<l) return inf;
if(T[q].lazy) lazy(q);
if(T[q].l>=l&&r<=T[q].r) return T[q].minm;
return min(Askmin(lc(q),l,r),Askmin(rc(q),l,r));
}
inline int Askmax(int q,int l,int r){
if(T[q].l>r || T[q].r<l) return inf;
if(T[q].lazy) lazy(q);
if(T[q].l>=l&&r<=T[q].r) return T[q].maxm;
return max(Askmax(lc(q),l,r),Askmax(rc(q),l,r));
}
}
//these are useless,TianYi do not know why she wrote it QAQ
int Log[N];
namespace ST{
ll minn[N][25];
inline void build(int n){
for_(i,1,n) {minn[i][0]=height[i];}
for_(j,1,20) {
for_(i,1,n-(1<<j)+1){
minn[i][j]=min(minn[i][j-1],minn[i+(1<<(j-1))][j-1]);
}
}
}
inline ll askLCP(ll i,ll j){
ll qwq=Log[j-i];
return min(minn[i+1][qwq],minn[j-(1<<qwq)+1][qwq]);
}
}
using namespace ST;
// the ST table is useful but not SegTree QAQ
stack<int> S;
set<ll> vis;
map<ll,ll> mp;
inline void In(){
int n;read(n);
_for(i,n,1){
read(a[i]);
}
for_(i,1,n)
san[i]=a[i];
sort(san+1,san+n+1);
int SAs=unique(san+1,san+n+1)-san-1;
for_(i,1,n)
a[i]=lower_bound(san+1,san+SAs+1,a[i])-san;
Init(a,n);Init_H(a,n);
Log[1]=0;
for_(i,2,n){
Log[i]=Log[i>>1]+1;
}
build(n);
vis.insert(inf) ;
vis.insert(-inf);
ll ans=0;
_for(i,n,1){
ans+=n-i+1;
ll p=*--vis.upper_bound(rk[i]);
ll q=*vis.lower_bound(rk[i]);
if (p!=-inf && q==inf) {ans-=askLCP(p,rk[i]);}
if (p==-inf && q!=inf) {ans-=askLCP(rk[i],q);}
if (p!=-inf && q!=inf) {ans-=max(askLCP(p,rk[i]),askLCP(rk[i],q));}
write(ans,'\n');
vis.insert(rk[i]);
}
}
}
using namespace solve;
P6793「SNOI2020」字符串
题意
给定两个长度为 \(n\) 的小写字符串 \(a, b\)，求出他们所有长为 \(k\) 的子串，分别组成集合 \(\text {A, B}\) ，每次可以修改 \(\text A\) 中一个元素的后缀，费用为后缀的长度，求将 \(\text A\) 修改成 \(\text B\) 的最小费用之和。
思路
首先依然是看到后缀，所以考虑使用后缀数组来解决这个问题
还是老样子，先把字符串连起来，然后用特殊字符隔开，然后我们可以很明显的发现对于 \(x\) 和 \(y\) 两个串，如果想要让其对应我们需要的费用为 \(k-\text {LCP}(x,y)+1\)
然后我们贪心的先把 \(\text{LCP}\) 较大的串都对应起来，用并查集维护即可
代码
代码
namespace solve{
int height[N],sa[N],oldsa[N],rk[N],oldrk[N];
ll cnt[N],key[N];
namespace SA{
inline bool cmp(ll x,ll y,ll w){
return (oldrk[x]==oldrk[y])&&(oldrk[x+w]==oldrk[y+w]);
}
inline void Init(char *s){
int n=strlen(s+1),m=128,tot;
for_(i,1,n)
rk[i]=s[i],
++cnt[rk[i]];
for_(i,1,m)
cnt[i]+=cnt[i-1];
_for(i,n,1) sa[cnt[rk[i]]--]=i;
for(ll w=1;;w<<=1,m=tot) {
tot=0;
_for(i,n,n-w+1)
oldsa[++tot]=i;
for_(i,1,n)
if(sa[i]>w)
oldsa[++tot]=sa[i]-w;
memset(cnt,0,sizeof(cnt));
for_(i,1,n)
++cnt[key[i]=rk[oldsa[i]]];
for_(i,1,m)
cnt[i]+=cnt[i-1];
_for(i,n,1)
sa[cnt[key[i]]--]=oldsa[i];
memcpy(oldrk+1,rk+1,n*sizeof(int));
tot=0;
for_(i,1,n)
rk[sa[i]]=((cmp(sa[i],sa[i-1],w))?(tot):(++tot));
if(tot==n)
break;
}
}
inline void Init_H(char *s){
int n=strlen(s+1),tot=0;
for_(i,1,n){
if(!rk[i]) continue;
if(tot) --tot;
while(s[i+tot]==s[sa[rk[i]-1]+tot]) ++tot;
height[rk[i]]=tot;
}
}
}
using namespace SA;
int Log[N];
namespace ST_table{
ll minn[N][20];
inline void build(int n){
for_(i,1,n) {minn[i][0]=height[i];}
for_(j,1,20) {
for_(i,1,n-(1<<j)+1){
minn[i][j]=min(minn[i][j-1],minn[i+(1<<(j-1))][j-1]);
}
}
}
inline ll askLCP(ll i,ll j){
ll qwq=Log[j-i];
return min(minn[i+1][qwq],minn[j-(1<<qwq)+1][qwq]);
}
}
//using namespace ST_Table;
int fa[N];
inline int find(int x){
return ((fa[x]==x)?x:fa[x]=find(fa[x]));
}
inline void merge(int x,int y){
fa[x]=y;
}
char s1[N],s2[N],s[N];
vector<int> vec[300005];
int cnt1[N];
inline void In(){
Log[1]=0;
for_(i,1,N-1) Log[i]=Log[i>>1]+1;
for_(i,1,N-1) fa[i]=i;
int n,k;read(n,k);
FastI>>(s1+1)>>(s2+1);
for_(i,1,2*n+1){
if(i==n+1) s[i]='#';
else if(i<=n) s[i]=s1[i];
else s[i]=s2[i-n-1];
}
int len=n*2+1;
Init(s),Init_H(s);
int ans=(n-k+1)*k;
for_(i,1,len){
cnt1[i]=0;
if(sa[i]<=n-k+1) cnt1[i]=1;
else if(sa[i]>n+1 && sa[i]<=len-k+1) cnt1[i]=-1;
if(i>1) vec[height[i]].push_back(i);
}
_for(i,n,0){
int sz=vec[i].size();
for_(j,0,sz-1){
int qwq=vec[i][j];
int x=find(qwq-1),y=find(qwq);
ans-=((cnt1[x]*cnt1[y]>0)?(0):(min(abs(cnt1[x]),abs(cnt1[y]))))*min(i,k);
cnt1[y]=cnt1[x]+cnt1[y];
merge(x,y);
}
}
write(ans,'\n');
}
}
using namespace solve;
CF955D Scissors
思路
首先考虑对于传进来的两个串 \(s_1\) 和 \(s_2\) ，预处理出 \(s_2\) 的每个前缀在 \(s_1\) 中出现的最早位置和 \(s_2\) 每个后缀在 \(s_1\) 中出现的最晚位置
然后直接扫一遍就行了，复杂度 \(\text O(n)\)
代码
点击查看代码
namespace solve{
const int N=5e5+5;
int mod=1e9,base=131;
int n,m,k,ans1,ans2,lm[N],rm[N];
char s[N],t[N];
class Hash{
public:
int Hash[N], poww[N];
inline void Init(char *s) {
int len=strlen(s+1);
poww[0]=1;
for_(i,1,len) {
Hash[i]=(Hash[i-1]*base+s[i]-'a'+1) % mod;
poww[i]=poww[i-1]*base%mod;
}
}
inline int get(int l, int r){
return ((Hash[r]-Hash[l-1]*poww[r-l+1])%mod+mod)%mod;
}
}S,T;
inline bool Judge(){
if (n<(k<<1)||m>(k<<1)) return 0;
S.Init(s),T.Init(t);
int pos=k;
for_(i,1,m) lm[i]=n+1;
for_(i,1,min(m,k)){
while(pos<=n&&S.get(pos-i+1,pos)!=T.get(1,i))
pos++;
if(S.get(k-i+1,k)==T.get(1,i))
pos=k;
lm[i]=pos;
}
pos=n-k+1;
for_(i,1,min(m,k)){
while(pos && S.get(pos, pos + i - 1) != T.get(m - i + 1, m)) pos--;
if(S.get(n-k+1,n-k+i)==T.get(m-i+1,m)) pos=n-k+1;
rm[m-i+1]=pos;
}
for_(i,1,n-m+1){
if(S.get(i,i+m-1)==T.get(1,m)){
if(k>=i&&n-k+1<=i+m-1) continue;
ans1=min(max(1ll,i-k+1),n-k+1-k);
ans2=max(k+1,min(n-k+1,i));
return 1;
}
}
for_(i,1,m-1){
if(lm[i]<rm[i+1]&&lm[i]<=n&&rm[i+1]){
ans1=lm[i]-k+1;
ans2=rm[i+1];
return 1;
}
}
return 0;
}
inline void In() {
srand(time(0));
mod+=rand();
base+=rand()%10;
read(n,m,k);
FastI>>(s+1)>>(t+1);
if(Judge())
write("Yes\n",ans1," ",ans2);
else
write("No");
}
}
CF1037H Security
题意
给定一个字符串 \(s\) 和 \(q\) 次询问，每次询问给出一个 \(l_i,r_i\) 和 \(x_i\)，你需要选出一个满足以下条件的字符串 \(str\)。
-
\(str\) 是 \(s[l_i\sim r_i]\) 的子串。
-
\(str > x_i\)。
-
\(str\) 是所有满足以下条件内字符串字典序最小的。
输出 \(str\) 的长度，如果不存在 \(str\) 则输出 \(-1\)。
思路
先把 \(s\) 和所有的询问 \(x_i\) 串都连起来，用小于 \(a\) 的字符连接，连成字符串 \(S\)
枚举 \(T\) 的前缀，判断区间中是否存在一个子串满足以下条件
-
这个子串等于这个前缀加上一个字母
-
加上的字母大于 \(T\) 的前缀的后面一个字符
如果前缀为 \(T\) 本身，那么后面一个字符是极小的。
在 \(\text {SA}\) 上二分出一个区间，满足区间中的后缀与 \(T\) 的 \(\text{LCP}\) 长度等于正在枚举的 \(T\) 的前缀长度 \(len\)，记录上次的二分结果
求这个区间中满足 \(sa_i\in [l,r-len]\) 的最小的 \(i\) ，用主席树或者扫描线维护，复杂度 \(\text O(|S| \log |S|)\)
代码
点击查看代码
namespace solve{
const int N=4e5+5;
char stp[N];
int s[N*2],n,len;
class SA{
public:
int sa[N*2],height[N*2],cnt[N*2],rk[N*2];
void S_sort(int *s,int l,int m){
int cnt1;
for_(i,1,l) cnt[height[i]=s[i]]++;
for_(i,2,m) cnt[i]+=cnt[i-1];
_for(i,l,1) sa[cnt[height[i]]--]=i;
For_(k,1,l,k){
cnt1=0;
for_(i,l-k+1,l) rk[++cnt1]=i;
for_(i,1,l)
if(sa[i]>k)
rk[++cnt1]=sa[i]-k;
for_(i,1,m) cnt[i]=0;
for_(i,1,l) cnt[height[i]]++;
for_(i,2,m) cnt[i]+=cnt[i-1];
_for(i,l,1) sa[cnt[height[rk[i]]]--]=rk[i],rk[i]=0;
swap(height,rk);
height[sa[1]]=m=1;
for_(i,2,l)
height[sa[i]]=m=m+!(rk[sa[i]]==rk[sa[i-1]]&&rk[sa[i]+k]==rk[sa[i-1]+k]);
if(m==l) return;
}
}
inline void build(int *s,int l,int m){
int k=0;
S_sort(s,l,m);
for_(i,1,l)
rk[sa[i]]=i;
for_(i,1,l){
if(rk[i]==1) k=0;
else{
if(k>0) k--;
int j=sa[rk[i]-1];
while(i+k<=l&&j+k<=l&&s[i+k]==s[j+k])
k++;
}
height[rk[i]]=k;
}
}
}a;
class SegTree{
public:
int t[N*4],d;
inline void build(int n){
for(d=1;d<n;d<<=1);
memset(t,0x7f,sizeof(t));
}
inline int ask(int l,int r){
int mn=2e9;
for(l=l+d-1,r=r+d+1;l^r^1;l>>=1,r>>=1){
if(l&1^1) mn=min(mn,t[l^1]);
if(r&1) mn=min(mn,t[r^1]);
}
return mn;
}
inline void add(int x,int v){
for(int i=x+d;i;i>>=1)
t[i]=v;
}
}T;
pair<int,int> q[N];
namespace ST_Table{
int val[N],l[N],ans[N],ansl[N],Log[N*2],ST[20][N*2];
inline int askmin(int l,int r){
int k=Log[r-l+1];
return min(ST[k][l],ST[k][r-(1<<k)+1]);
}
}
using namespace ST_Table;
namespace Solve{
class node{
public:
int w,l,r,id,len;
};
vector<node> que[N*2];
inline void ask(int l,int r,int val,int slen,int id){
int w,cnt2=a.rk[val];
for(int j=1<<20;j;j>>=1)
((cnt2+j<=len)&&(askmin(a.rk[val]+1,cnt2+j)>=(min(slen,r-l)+1)))&&(
cnt2+=j
);
_for(i,min(slen,r-l),0){
w=cnt2;
for(int j=1<<20;j;j>>=1)
((w+j<=len)&&(askmin(cnt2+1,w+j)>=i))&&(
w+=j
);
que[cnt2+1].push_back(node{w,l,r-i,id,i});
cnt2=w;
}
}
inline void solve(){
T.build(l[0]);
int tp,id;
_for(i,len,1){
(a.sa[i]<=l[0])&&(T.add(a.sa[i],i),0);
int len1=que[i].size();
for_(j,0,len1-1)
(que[i][j].len>ansl[id=que[i][j].id]&&(tp=T.ask(que[i][j].l,que[i][j].r))<=que[i][j].w)&&(
ans[id]=a.sa[tp],ansl[id]=que[i][j].len,
0
);
}
}
}
using namespace Solve;
inline void In(){
memset(ansl,-1,sizeof(ansl));
int m;
FastI>>stp>>m;
l[0]=strlen(stp);
for_(i,0,l[0]-1)
s[++len]=stp[i];
s[++len]='z'+1;
for_(i,1,m){
read(q[i].first,q[i].second);
FastI>>stp;
l[i]=strlen(stp),val[i]=len+1;
for_(j,0,l[i]-1)
s[++len]=stp[j];
s[++len]='a'-1;
}
a.build(s,len,'z'+1);
for_(i,2,len)
ST[0][i]=a.height[i];
for(int j=1;(1<<j)<=len;j++)
for_(i,1,len-(1<<j)+1)
ST[j][i]=min(ST[j-1][i],ST[j-1][i+(1<<j-1)]);
for_(i,2,len)
Log[i]=Log[i>>1]+1;
for_(i,1,m)
ask(q[i].first,q[i].second,val[i],l[i],i);
solve();
for_(i,1,m){
if(ans[i]){
for_(j,ans[i],ans[i]+ansl[i])
write(char(s[j]));
write("\n");
}
else
write("-1\n");
}
}
}
using namespace solve;
P1117「NOI2016」优秀的拆分
题意
求一个字符串所有的子串可以拆成 \(\text{AABB}\) 的本质不同的形式个数，其中 \(\text{A,B}\) 均为任意非空字符串
多组测试
思路
多测不清空，亲人两行泪
之前听说过好几次这道 \(\text{NOI2016}\) 的后缀数组好题，所以直接考虑如何使用后缀数组来解决这道题
题目要求 \(\mathbf{AABB}\) 的数量，我们拆分问题可以转化为求每个点相邻的 \(\mathbf{AA}\) 串的数量（以这个点为头或以这个点为尾）
定义 \(pre_i\) 以 \(s[i]\) 为结尾的 \(\mathbf{AA}\) 串的数量，\(nxt_i\) 为以 \(s[i]\) 开头的 \(\mathbf{AA}\) 串的数量
这样我们就可以把两个相连的 \(\mathbf{AA}\) 的合并成一个 \(\mathbf{AABB}\) 的拆分，答案为 \(ans=\sum\limits_{i=1}^{n-1} pre_{i+1} \times nxt_i\)
可暴力求明显是 \(O(n^2 log n)\) 的，会超时
我们枚举 \(len\) 代表 \(\mathbf{AA}\) 形子串的 \(\dfrac{1}{2}\) 长度，然后判断 \(\text{LCP}\) 和 \(\text{LCS}\)，然后
代码
P5048【 YnOI2019 模拟赛】Yuno loves sqrt technology II
查询区间逆序对，要求时间小于 \(\mathcal O(n^{\frac{3}{2}})\)，空间 \(\mathcal O(n)\)
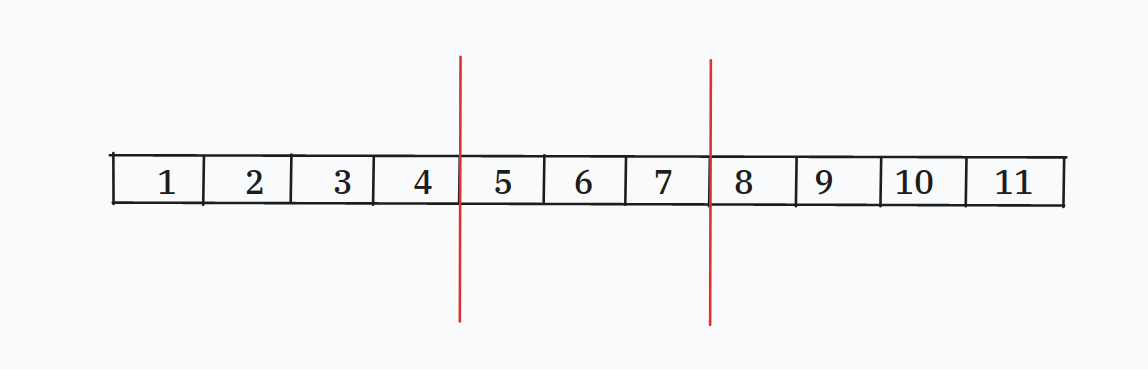
假设我们现在的区间是 \([l,r]\)，也就是图中红色的部分
现在我们需要向右移动一格
这一次的移动为我们带来的贡献是 \([1\sim r]\) 内大于 \(\mathbf{val}(r+1)\) 的数量减去\([1\sim l-1]\) 内大于 \(\mathbf{val}(r+1)\)
用图中的数字来表示就是 \([1\sim 7]\) 内值大于 \(\mathbf{val(8)}\) 的数量 减去 \([1\sim 4]\) 内大于 \(\mathbf{val}(8)\) 的数量
考虑第一个(也就是 \([1\sim r]\) 内大于 \(\mathbf{val}(r+1)\) 的数量)是定值，可以直接预处理，但是在后面那个里 \(l\) 是不确定的，我们无法直接预处理，所以这个也就是主要要维护的地方
我们可以首先先对于每个位置都开一个 \(\mathbf{vector}\) 来维护，把当前询问的编号和 \(r+1\) 扔到 \(l\) 所在的 \(\mathbf{vector}\) 里，进行第二次离线
莫队一共会移动端点 \(\mathcal O(n\sqrt n)\) 次，内存较大
我们发现，从 \(r\) 移动到我们想要移动的 \(r_1\) 时 \(l\) 不会发生变化，所以我们可以直接把 \(\{r+1 \sim r_1\}\) 扔到 \(\mathbf{vector}\) 内，这样空间就是 \(\mathcal O(n)\) 的了
然后可以值域分块，单次 \(\mathcal O(1)\) 修改 \(\mathcal O(\sqrt n )\) 查询，但是我们发现我们有 \(n\sqrt n\) 次询问和 \(n\) 次修改
所以我们适当增加修改的复杂度至 \(\mathcal O(\sqrt n)\) ，借此将查询的复杂度降为 \(\mathcal O(1)\)
总复杂度 \(\mathcal O(n \log n+n \sqrt n)\)，空间 \(\mathcal O(n)\)
按照上面的区间逆序对问题来实现即可
特殊的，本题因为是 \(\mathbf{YnOI}\) 所以比较卡常，不能#define int long long不然会 TLE
FastIO都救不回来那种
点击查看代码
#include<bits/stdc++.h>
#include <sys/mman.h>
#define N 100010
#define firein(a) freopen(a".in","r",stdin)
#define fireout(a) freopen(a".out","w",stdout);
#define fire(a) firein(a),fireout(a)
#define for_(a,b,c) for(int a=b;a<=c;a++)
#define _for(a,b,c) for(int a=b;a>=c;a--)
#define For_(a,b,c,d) for(int a=b;a<=c;a+=d)
#define _For(a,b,c,d) for(int a=b;a>=c;a-=d)
using namespace std;
namespace Solve{
const char *I=(char*)mmap(0,1<<22,1,2,0,0);
inline int read() {
int x=0,f=0;
while(*I<48)f|=*I++==45;
while(*I>47)x=x*10+(*I++&15);
return f?-x:x;
}
char O[1<<22],*o=O;
void print(long long x) {
if(x<0)*o++=45,x=-x;
if(x>9)print(x/10);
*o++=48+x%10;
}
struct Query{
int l,r,v,id;
}q[N];
vector<Query> L[N],R[N];
int n,m,blo,a[N],b[N],c[N],d[N],mp[N],tot,pos[N],bL[N],bR[N];
long long sum1[N],sum2[N],ans[N],Ans[N];
inline bool cmp(const Query &a,const Query &b){
if((a.l-1)/blo!=(b.l-1)/blo) return (a.l-1)/blo<(b.l-1)/blo;
return a.r<b.r;
}
namespace BIT{
#define lowbit(x) ((x)&(-x))
inline void Add(int x,int v){
For_(i,x,n,lowbit(i))
b[i]+=v;
}
inline int Ask(int x){
int ans=0;
_For(i,x,1,lowbit(i)){
ans+=b[i];
}
return ans;
}
}
using namespace BIT;
inline void Solve(){
sort(q+1,q+m+1,cmp);
q[0].l=1;
for_(i,1,m){
ans[i]=sum1[q[i].r]-sum1[q[i-1].r]+sum2[q[i].l]-sum2[q[i-1].l];
if(q[i-1].r<q[i].r) {
L[q[i-1].l-1].push_back({q[i-1].r+1,q[i].r,-1,i});
}
if(q[i].r<q[i-1].r) {
L[q[i-1].l-1].push_back({q[i].r+1,q[i-1].r,1,i});
}
if(q[i].l<q[i-1].l) {
R[q[i].r+1].push_back({q[i].l,q[i-1].l-1,-1,i});
}
if(q[i-1].l<q[i].l) {
R[q[i].r+1].push_back({q[i-1].l,q[i].l-1,1,i});
}
}
}
void In(){
n=read(),m=read();
blo=sqrt(n)+1;
for_(i,1,n) {
a[i]=read();
mp[i]=a[i];
}
sort(mp+1,mp+n+1);
tot=unique(mp+1,mp+n+1)-mp-1;
for_(i,1,n)
a[i]=lower_bound(mp+1,mp+tot+1,a[i])-mp;
for_(i,1,n){
sum1[i]=sum1[i-1]+i-1-Ask(a[i]);
Add(a[i],1);
}
memset(b,0,sizeof(b));
_for(i,n,1){
sum2[i]=sum2[i+1]+Ask(a[i]-1);
Add(a[i],1);
}
for_(i,1,m){
q[i].l=read();
q[i].r=read();
q[i].id=i;
}
Solve();
for_(i,1,1e5){
pos[i]=(i-1)/blo+1;
if(pos[i]!=pos[i-1]) {
bL[pos[i]]=i;
bR[pos[i-1]]=i-1;
}
}
bR[pos[(int)1e5]]=1e5;
int sum,l,r,v,id;
for_(i,1,n){
for_(j,1,pos[a[i]]-1)
c[j]++;
for_(j,bL[pos[a[i]]],a[i])
d[j]++;
int Size=L[i].size();
for_(j,0,Size-1){
l=L[i][j].l;
r=L[i][j].r;
v=L[i][j].v;
id=L[i][j].id;
sum=0;
for_(k,l,r)
sum+=c[pos[a[k]+1]]+d[a[k]+1];
ans[id]+=v*sum;
}
}
memset(c,0,sizeof(c));
memset(d,0,sizeof(d));
_for(i,n,1){
for_(j,pos[a[i]]+1,blo)
c[j]++;
for_(j,a[i],bR[pos[a[i]]])
d[j]++;
int Size=R[i].size();
for_(j,0,Size-1){
l=R[i][j].l;
r=R[i][j].r;
v=R[i][j].v;
id=R[i][j].id;
sum=0;
for_(k,l,r)
sum+=c[pos[a[k]-1]]+d[a[k]-1];
ans[id]+=v*sum;
}
}
for_(i,1,m){
ans[i]+=ans[i-1];
Ans[q[i].id]=ans[i];
}
for_(i,1,m)
print(Ans[i]),*o++='\n';
fwrite(O,1,o-O,stdout);
}
}
using namespace Solve;
signed main(){
#ifndef ONLINE_JUDGE
fire("data");
#endif
In();
}
P4887 第十四分块(前体)
点缀光辉的第十四分块(前体)，分块不可做，二次离线莫队
首先分析题面，考虑对于每次进行移动，贡献是 \(\{1\sim r\}\) 内和 \(\mathbf{val}(r+1)\) 异或和中 \(1\) 的个数 减去 \(\{1\sim l-1\}\) 内和 \(\mathbf{val}(r+1)\) 异或和中 \(1\) 的个数
前面依然是预处理，后面的直接 vector 存进去，和上一道题一样
然后我们发现，后面的值域分块维护，解决
数组开 \(100010\)，交上去，诶 \(\mathbf{wa}\) 了，调了半天发现只要改到 \(200020\) 就能过
不过这道题似乎不是很卡常，没用 Fread 和 Fwrite 也过了，直接关同步流 cin/cout
点击查看代码
#define ONLINE_JUDGE
#include<bits/stdc++.h>
#include<sys/mman.h>
#include<fcntl.h>
#define N 200010
#define firein(a) freopen(a".in","r",stdin)
#define fireout(a) freopen(a".out","w",stdout);
#define fire(a) firein(a),fireout(a)
#define for_(a,b,c) for(int a=b;a<=c;a++)
#define _for(a,b,c) for(int a=b;a>=c;a--)
#define For_(a,b,c,d) for(int a=b;a<=c;a+=d)
#define _For(a,b,c,d) for(int a=b;a>=c;a-=d)
#define lowbit(x) ((x)&(-x))
#define int long long
typedef long long ll;
using namespace std;
namespace Solve{
// #ifndef ONLINE_JUDGE
// int _if=open("data.in",O_RDONLY);
// FILE* _of=fopen("data.out","w");
// #else
// int _if=fileno(stdin);
// FILE* _of=stdout;
// #endif
// const char *_I=(char*)mmap(0,1<<24,1,2,_if,0);
// inline ll read(){
// int x=0;
// while(*_I<48)++_I;
// while(*_I>47)x=x*10+(*_I++&15);
// return x;
// }
// char O[1<<24],*o=O;
// void print(ll x){
// if (x>9)print(x/10);
// *o++=x%10+48;
// }
int a[N],bl[N],st[N],blo,top,n,m,k;
ll s1[N],s2[N],s[N],ret[N],ans[N],res;
struct node{
int l,r,id;
inline node(){}
inline node(int L,int R,int Id):l(L),r(R),id(Id){}
inline bool operator <(const node &b)const{
return bl[l]==bl[b.l]?r<b.r:l<b.l;
}
}q[N];
inline void Init(){
int Cnt,X;
for(int i=0;i<16384;++i){
Cnt=0,X=i;
for(;X;X^=lowbit(X))
++Cnt;
if(Cnt==k)
st[++top]=i;
}
}
vector<node>Q[N];
inline void Solve1(){
int l=q[1].r+1,r=q[1].r;
for_(i,1,m){
if(l<q[i].l){
Q[r].push_back(node(l,q[i].l-1,q[i].id<<1));
}
if(l>q[i].l){
Q[r].push_back(node(q[i].l,l-1,q[i].id<<1));
}
l=q[i].l;
if(r<q[i].r){
Q[l-1].push_back(node(r+1,q[i].r,q[i].id<<1|1));
}
if(r>q[i].r){
Q[l-1].push_back(node(q[i].r+1,r,q[i].id<<1|1));
}
r=q[i].r;
}
}
inline void Solve2(){
int l=q[1].r+1,r=q[1].r;
for_(i,1,m){
if(l<q[i].l)
res-=ret[q[i].id<<1]-s2[q[i].l-1]+s2[l-1];
if(l>q[i].l)
res+=ret[q[i].id<<1]-s2[l-1]+s2[q[i].l-1];
l=q[i].l;
if(r<q[i].r)
res+=s1[q[i].r]-s1[r]-ret[q[i].id<<1|1];
if(r>q[i].r)
res-=s1[r]-s1[q[i].r]-ret[q[i].id<<1|1];
r=q[i].r;
ans[q[i].id]=res;
}
}
inline void In(){
std::ios::sync_with_stdio(false);
cin.tie(nullptr);cout.tie(nullptr);
cin>>n>>m>>k;
blo=800;
Init();
for_(i,1,n){
cin>>a[i];
bl[i]=(i-1)/blo+1;
}
for_(i,1,m){
cin>>q[i].l>>q[i].r;
q[i].id=i;
}
sort(q+1,q+1+m);
Solve1();
for_(i,1,n){
s1[i]=s1[i-1]+s[a[i]];
for_(k,1,top)
++s[a[i]^st[k]];
s2[i]=s2[i-1]+s[a[i]];
for(vector<node>::iterator it=Q[i].begin();it!=Q[i].end();++it)
for_(k,it->l,it->r)
ret[it->id]+=s[a[k]];
}
Solve2();
for_(i,1,m)
cout<<ans[i]<<endl;
}
}
using namespace Solve;
signed main(){
// fire("data");
In();
}
