【学习笔记】字符串基础:后缀数组
yspm讲课内表示不会可以哈希+二分
最后还是听了不知道从 ftp 里搞出来的 yspm 讲课视频才听懂的,但是 yspm 用的屏幕绘画是看不见的比较尊贵,然后开了画图
本文约定字符串下标从 \(1\) 开始
后缀数组
后缀数组,即 \(\text{SA(Suffix Array)}\),主要关系到两个数组:
-
\(sa\)
对于 \(sa_i\) 表示将所有后缀排序后第 \(i\) 小的后缀的编号,也就是排名为 \(i\) 的后缀的位置
此处的排序是按照字典序排的
-
\(rk\)
\(rk_i\) 表示从第 \(i\) 个位置开始的后缀的排名
根据定义我们发现两个数组满足以下性质 \(sa[rk_i]=rk[sa_i]=i\),两者是互逆的
借用 \(\text{OI-wiki}\) 的一张图用于解释后缀数组内的 \(sa\) 和 \(rk\) 数组

求后缀数组
-
\(\text O(n^2\log n)\)
最为暴力的想法
直接大力
sort排序,不难发现排序需要进行 \(\text O(n\log n)\) 次字符串比较,每次比较复杂度均为 \(\text O(n)\),所以是 \(\text O(n^2\log n)\)的这个很明显非常不优,肯定是不推荐的
-
\(\text O(n \log^2n)\)
倍增做法
首先对字符串 \(s\) 的所有长度为 \(1\) 的子串进行排序,得到排序后的编号数组 \(sa_1\) 和排名数组 \(rk_1\)。
用两个连起来的长度为 \(1\) 的子串作为排序的两个关键字(靠前的子串为第一关键字)进行排序,这样就可以获得长度为 \(2\) 的子串排序的结果
然后我们再用两个长度为 \(2\) 的子串作为排序的两个关键字排序,以此类推,假设倍增后长度为 \(w\) 则当 \(i+w\) 加起来比 \(n\) 大的时候视 \(s_{i+w}\) 为无限小
在最后我们倍增出来的长度已经大于等于 \(n\) 的时候就可以得到我们需要的后缀数组 \(sa\)
显然倍增的过程是 \(\text O(\log n)\) ,而每次倍增用
sort对子串进行排序是 \(\text O(n\log n)\) ,而每次子串的比较花费 \(2\) 次字符比较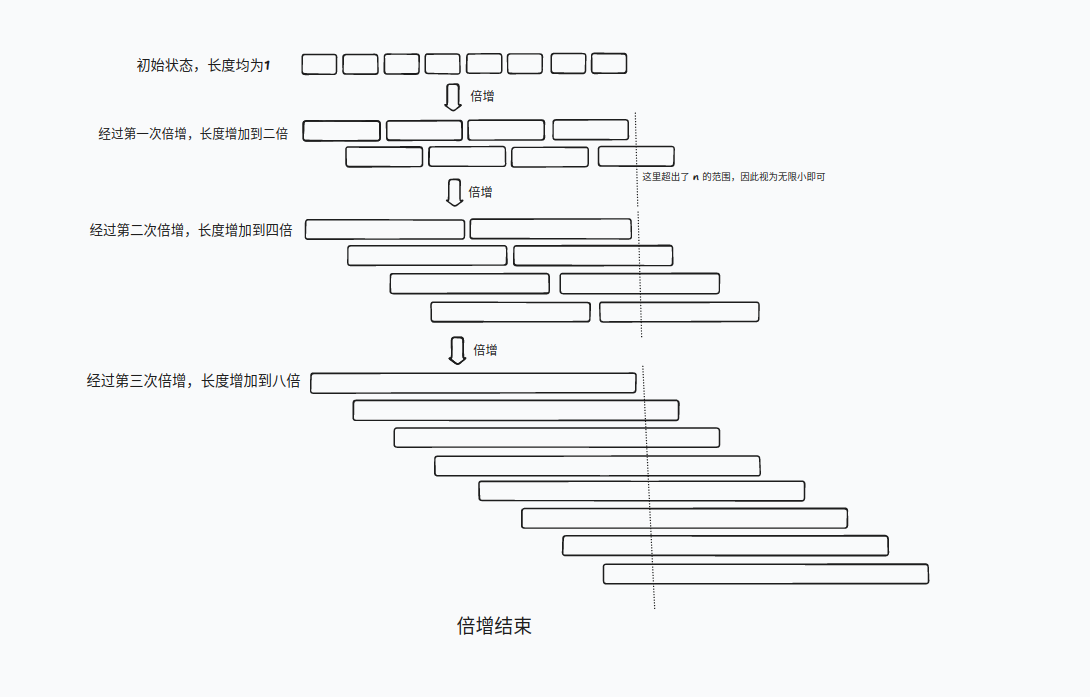
这个看起来就优多了,复杂度是 \(\text{O}(n \log^2 n)\) 的
点击查看代码
namespace SA{ int sa[N],rk[N],oldrk[N]; inline bool cmp(int x,int y,int w){ return (rk[x]!=rk[y])?(rk[x+w]<rk[y+w]):(rk[x]<rk[y]); } inline void Init(char *s){ int n=strlen(s+1); for_(i,1,n){ sa[i]=i; rk[i]=s[i]; } for(int w=1;w<n;w<<=1){ sort(sa+1,sa+1+n,cmp); memcpy(oldrk,rk,sizeof(rk)); int tot=0; for_(i,1,n){ if(oldrk[sa[i]]==oldrk[sa[i-1]]&&oldrk[sa[i]+w]==oldrk[sa[i-1]+w]) rk[sa[i]]=tot; else rk[sa[i]]=++tot; } } } } using namespace SA;解释一下代码
首先
cmp是双关键字的,这是因为字典序排的没啥好说的为什么我们要复制一遍
rk呢?(oldrk)这很明显是因为在计算同时也在修改
rk,原本的rk会被覆盖最后的判断是因为如果两个子串的字典序相同我们则需要去重
-
\(\text{ O}(n \log n)\)
虽然上面那份代码已经可以通过 LOJ 的后缀排序,但我们还是认为 \(\text O(n \log^2 n)\) 不够优怎么办?发现主要瓶颈在于 \(\text O(n \log n)\) 的
sort排序我们发现后缀数组的排序是双关键字,而且值域是排名也就是严格 \(\text O(n)\) 的
所以可以使用基数排序来优化我们上面的倍增做法,这样我们就可以得到一份常数巨大的 \(\text O(n \log n)\) 做法(其实是因为我狂暴
memset而且数组开的巨大的原因)常数巨大到连 \(\text O(n \log^2 n)\) 都跑不过,甚至很可能会T掉,因此我们进行需要常数优化
-
第二关键字无需基数排序
第二关键字排序的实质其实就是把超出字符串范围的 \(sa_i\) 放到 \(sa\) 数组头部,剩下的依原顺序放入
因此我们完全可以直接完成而不是基数排序
-
优化计数排序的值域
我们在计算完 \(rk\) 只会就会留下一个 \(tot\),这个 \(tot\) 就是当前排序的值域,可以来跑基数排序而不再用 \(n\)
这两个(尤其是第二个)优化非常显著,这样就可以跑过 \(\text O(n \log^2 n)\) 了,跑不过就是写假了,因为常数很小
点击查看代码
namespace SA{ int sa[N],rk[N],oldrk[N],oldsa[N],w,cnt[N],key[N]; inline bool cmp(int x,int y,int w){ return (oldrk[x]==oldrk[y])&&(oldrk[x+w]==oldrk[y+w]); } inline void Init(char *s){ int n=strlen(s+1),m=127,tot; for_(i,1,n) rk[i]=s[i], ++cnt[rk[i]]; for_(i,1,m) cnt[i]+=cnt[i-1]; _for(i,n,1) sa[cnt[rk[i]]--]=i; for(int w=1;;w<<=1,m=tot) { tot=0; _for(i,n,n-w+1) oldsa[++tot]=i; for_(i,1,n) if(sa[i]>w) oldsa[++tot]=sa[i]-w; memset(cnt,0,sizeof(cnt)); for_(i,1,n) ++cnt[key[i]=rk[oldsa[i]]]; for_(i,1,m) cnt[i]+=cnt[i-1]; _for(i,n,1) sa[cnt[key[i]]--]=oldsa[i]; memcpy(oldrk+1,rk+1,n*sizeof(int)); tot=0; for_(i,1,n) rk[sa[i]]=((cmp(sa[i],sa[i-1],w))?(tot):(++tot)); if(tot==n) break; } } } using namespace SA;这里有一些可以卡常的点,但是意义不大
-
将 \(rk[oldsa_i]\) 存下来,减少不连续内存访问
-
用函数来计算是否重复减少不连续内存访问
-
-
\(\text O(n)\)
一般是用不到的,\(\text O(n)\) 做法虽然跑的比倍增要快但是空间和码量都巨大
有两种做法,
SA-IS和DC3,我都不会
\(\text{height}\) 数组
定义
首先我们要进行一些定义
-
后缀 \(i\)
我们为了方便把从 \(i\) 开始的后缀称为后缀 \(i\)
-
\(\text{LCP}\) (最长公共前缀)
\(\text{LCP}(x,y)\) 是指字符串 \(x\) 与字符串 \(y\) 的最长公共前缀(的长度),在这里指后缀 \(x\) 与后缀 \(y\) 的最长公共前缀(的长度)
-
\(\text{height}\) 数组的定义
\(height_i=\text {LCP}(sa_i,sa_{i-1})\) ,即第 \(i\) 名的后缀与它前一名的后缀的最长公共前缀
\(height_1=0\),因为没有在其前面的了
-
update
通过聆听 yspm 的讲解我发现我写的这里有一处问题,就是我这里的 \(\text{height}\) 数组应该叫做 \(\text h\) 数组
两者之间存在一定差异
-
关系
\(\text {height}\) 数组与 \(\text h\) 数组的关系如下
\(\text{height}[rk_i]=h[i]\)
也就是说事实上 \(\text h\) 数组才是排名 \(i\) 的后缀和排名 \(i-1\) 的后缀之间的LCP,而 \(\text{height}\) 数组却是后缀 \(i\) 和后缀 \(i-1\) 的 \(\text{LCP}\)
但是一般用不到 \(\text {height}\) 数组所以我们把 \(\text h\) 数组叫做 \(\text{height}\) 数组基本不会产生歧义
本文所有的 \(\text{height}\) 数组均为 \(\text h\) 数组
-
-
\(\text{LCP}\)性质及其证明
\(\text{LCP Lemma}\)
这个是重要性质,下面证明 \(\text{LCP Theorem}\) 要用
-
概念:
\[\text{LCP}(x,y)=\min_{x\le i<j<k\le y}\{\text {LCP}(i,j),\text{LCP}(j,k)\} \] -
证明
假设 \(\min(\text {LCP}(i,j),\text {LCP}(j,k))=p\)
我们可以得知后缀 \(i\) 和后缀 \(j\) 前 \(p\) 个字符相同,后缀 \(j\) 和后缀 \(k\) 前 \(p\) 个字符相同
所以可以得知后缀 \(i\) 和后缀 \(j\) 的前 \(p\) 个字符相同
接下来用反证法,假设 \(\text{LCP}(i,k)>p\)
根据假设我们可以得知后缀 \(i\) 的第 \(p+1\) 位一定和后缀 \(k\) 的第 \(p+1\) 位相同,后缀 \(i\) 和后缀 \(k\) 的第 \(p+1\) 位一定和后缀 \(j\) 的第 \(p+1\) 位不同
因为在 \(sa\) 数组内三者的前 \(p\) 位相同,因此我们可以得知后缀 \(i\) 的第 \(p+1\) 位$\le $后缀 \(j\) 的第 \(p+1\) 位 \(\le\) 后缀 \(k\) 的第 \(p+1\) 位
我们知道 \(i\) 和 \(k\) 的第 \(p+1\) 位相同,一次 \(j\) 的第 \(p+1\) 位一定也相同
而这样就和条件相互违背,因此 \(\text{LCP}(i,k)>p\) 不成立
得证
\(\text {LCP Theorem}\)
-
概念
\[\text{LCP}(x,y)=\min_{x< i\le y}\{\text {LCP}(i-1,i)\} \]当然也可以写成
\[\text{LCP}(x,y)=\min_{x< i\le y}\{\text {height}_i\} \] -
证明
首先我们可以把 \(\text{LCP}(x,y)\) 拆成两部分:\(\text {LCP}(x,x+1)\) 和 \(\text{LCP}(x+1,y)\)
根据 \(\text{LCP Lemma}\) 可知 \(\text {LCP}(x,y)=\min(\text {LCP}(x,x+1),\text{LCP}(x+1,y))\),显然正确
而后我们可以把后面的 \(\text {LCP(x+1,y)}\) 继续拆成 \(\text{LCP}(x+1,x+2)\) 和 \(\text{LCP}(x+2,y)\)
以此类推,根据数学归纳法得证
实现
实现 \(\text O(n)\) 求 \(\text{height}\) 数组需要一个引理
- \(height[{rk_{i}}]\ge height[{rk_{i-1}-1}]\)
这个引理非常好啊,让人脑洞大开(物理)
下面是证明
-
update
最上面的两个性质我在上面证明了,这个图我就不改了

当我们知道这个引理之后我们就可以暴力通过引理求 \(\text{height}\) 数组了
inline void Init_H(){
int tot=0;
for_(i,1,n){
if(rk[i]==0) continue;
if(tot) --tot;
while(s[i+tot]==s[sa[rk[i]-1]+tot]) ++tot;
height[rk[i]]=tot;
}
}
\(k\) 不会超过 \(n\) ,因此最多减 \(n\) 次,所以最多也就只会加 \(2n\) 次
复杂度是严格 \(\text{O}(n)\) 的
应用
这里摘自 \(\text{OI-wiki}\) 并乱改了一番
-
两子串最长公共前缀
这个我们直接上 \(\text{height}\) 数组,根据 \(\text{LCP Theorem}\) 所以显然正确
然后就转化成了 \(\text{RMQ}\) 问题,随便用个东西维护一下就行,推荐使用 \(\text{ST}\) 表来 \(\text O(1)\) 查
-
比较一个字符串的两个子串的大小关系
假设比较的是 \(S_1=S\{a\sim b\}\) 和 \(S_2=S\{c\sim d\}\) 两个子串
如果 \(\text {LCP}(a,c)\ge \min(|S_1|,|S_2|)\),满足 \(|S_1|>|S_2|\) 则 \(S_1>S_2\),也就是两者长度较长的比较大
否则如果 \(rk_{S_1}>rk_{S_2}\) 则 \(S_1>S_2\),也就是 \(rk\) 数组较大的比较大
-
理解
容易发现当 \(\text{LCP}(a,c)\ge \min(|S_1|,|S_2|)\) 时\(S_1\)和\(S_2\)内肯定有一个已经被全部比较完的情况下与另一个比较的结果是完全相同的
因为只要超出了原本长度就会自动视为无限小,所以长度较长的较大
因为已经判断完会不会有一大片都是完全一样了,所以此时直接对 \(rk\) 数组进行比较即可
-
-
计算不同的子串个数
计算可以相同的子串个数很明显是 \(\large \frac{n(n+1)}{2}\),只要让可以相同的减去相同的子串个数即可
我们知道子串其实就是后缀的前缀,所以我们可以直接按照后缀排序的顺序去枚举后缀,然后每次新增的子串其实就减去与上一个相比的 \(\text{LCP}\)
而 \(\text{LCP}\) 不用处理,因为在 \(\text{LCP}\) 最开始出现的时候就已经被记录为并非重复的子串
因此最后的结果就是 \(\frac{n(n+1)}{2}-\sum\limits_{i=2}^{n}\text{height}_i\)
-
出现至少 \(k\) 次的子串的最大长度
我们知道出现至少 \(k\) 次代表着至少有 \(k\) 个后缀以之为前缀
所以只要查询每相邻的 \(k-1\) 个 \(\text{height}\) 数组的最小值,最后在所有我们查询出来的取一个最大值即可
这样就又转化成了 \(\text{RMQ}\) 问题,随便糊一个上去就行
题目
后缀数组的题目非常多啊,我们一一列举
-
这个是模板题,没啥好说的直接求即可
-
模板题,不知道为什么说普通的 \(\text O(n)\) 过不去,但是 \(O(n \log n)\) 直接过去了
哦哦 SPOJ 换机子了,那不说啥了
-
最暴力的思路就是直接暴力比较子串和子串,复杂度 \(O(n^2)\)
但是我们直接就发现实际上求得是 \(\text{height}\) 数组最大值
因为BZOJ交不了所以我没写,口胡的思路
-
都说是 \(\text{SA}\) 板子题,但是我一眼没看出来,菜
哦我读假题了,这里其实是长度为 \(n\) 的一堆子串而不是全排序
仔细看一看就可以发现其是一个环,然后把环直接大力展开,这样我们就得到了一个二倍长度的字符串
然后我们就可以跑后缀数组了,求出 \(sa\) 之后直接大力判其后缀有没有第 \(n\) 个后缀即可,复杂度 \(\text O(n \log n)\) 完全可过
-
核心代码
inline void In(){ scanf("%s",s+1); int len=strlen(s+1); for_(i,1,len) s[i+len]=s[i]; Init(s); int newlen=strlen(s+1); for_(i,1,newlen){ if(sa[i]+len>2*len) continue; putchar(s[sa[i]+len-1]); } }
-
-
做的第一道不是板子的后缀数组题纪念
先前后作差求出其差值也就是新的字符串,然后把所有串连接在一起,用后缀数组求出\(\text{LCP}\),然后二分长度,每次从头到尾扫一遍
代码比较冗长
-
核心代码
inline void In(){ n=read(); for_(i,1,n){ l[i]=read(); for(int j=1;j<=l[i];++j){ a[i][j]=read(); if(j>1)mx=max(mx,a[i][j]-a[i][j-1]); } rt=min(rt,l[i]); } for(int i=1;i<=n;++i){ for(int j=2;j<=l[i];++j){ b[++tot]=a[i][j]-a[i][j-1]; id[tot]=i; } b[++tot]=++mx; } for_(i,1,tot){ mn=min(mn,b[i]); } for_(i,1,tot){ b[i]=b[i]-mn+1; mx=max(mx,b[i]); } Init(); Init_H(); while(lt<=rt){ if(check(mid=(lt+rt)>>1)) ans=mid+1,lt=mid+1; else rt=mid-1; } print(ans,"\n"); }
-
-
这个题目看起来就非常板啊,首先我们发现前面两项其实是定值,为 \(\frac{n(n-1)(n+1)}{2}\),没啥好说的
然后后面的 \(\text{LCP}\) 如何维护呢?
在我对 \(\text{height}\) 数组引理证明时用了两个定理
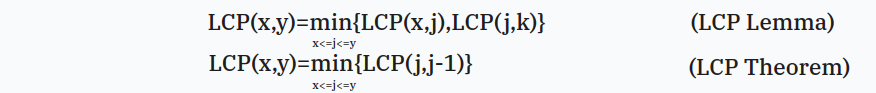
这两个定理随便挑一个再肆意转化一下就能发现 \(\text{LCP}(i,j)\) 其实就是 \(\min\{height[rk_i+1]\sim height[rk_j]\}\),然后这样就是一个非常经典的单调栈问题了
-
核心代码
inline void In(){ scanf("%s",s+1); Init(s); Init_H(s); int n=strlen(s+1),ans=0; for_(i,1,n){ while(height[STA[top]]>height[i]) --top; l[i]=i-STA[top]; STA[++top]=i; } STA[++top]=n+1; height[n+1]=-1; _for(i,n,1){ while(height[STA[top]]>=height[i])--top; ans-=2*height[i]*l[i]*(STA[top]-i); STA[++top]=i; } print(ans+n*(n-1)*(n+1)/2,"\n"); }
-
-
CF1073G Yet Another LCP Problem
这个题一眼看过去和上个题很像,直接建 \(\text{ST}\) 表,然后跑单调栈似乎就过去了,复杂度 \(\text O(n \log n)\) 完全可过
先建立后缀数组,我们查询 LCP 时依然要用到重要引理
\[LCP(i,j)=\min_{i<x\le j}\{height_x\} \]然后挂个 \(\text{ST}\) 表来 \(O(1)\) 查询,然后暴力枚举是 \(\text{O}(n^2)\) 会被卡,所以我们再挂个单调栈即可
-
一眼看过去似乎没什么思路,但是发现用AC自动机可以随便搞啊!但是这是后缀数组题单所以我要用后缀数组(悲
发现\(n\)和\(m\)的范围很小,所以可以用一个非常暴力的思路来解决这个题
先把所有串连起来跑一个后缀数组,然后对每一个询问向前、向后扫描并把答案放入
set,set判重并输出size异常暴力的思路,还真能过
-
你咋是绿题啊?这么菜,这不是 \(\text{SA}\) 吗,\(\text{SA}\) 板子不是紫吗
这个是板子,直接先跑后缀数组,然后按照后缀排序之后去求出 \(\text{height}\) 数组
然后去查询 \(\text{LCP}\),求出每 \(k-1\) 个数之间的 \(\text{LCP}\) 的 \(\min\)
此时再在所有查出来的 \(\text{LCP}\) 内取 \(\max\) 即可
-
核心代码
int val[N]; inline void In(){ int n=read(),k=read()-1; for_(i,1,n) val[i]=read(); Init(val,n);Init_H(val,n); deque<int> q; for_(i,2,k+1){ while(!q.empty()&&height[i]<=height[q.back()]) q.pop_back(); q.push_back(i); } int ans=height[q.front()]; for_(i,k+2,n){ while(!q.empty()&&i-q.front()>=k) q.pop_front(); while(!q.empty()&&height[i]<=height[q.back()]) q.pop_back(); q.push_back(i); ans=max(ans,height[q.front()]); } print(ans,"\n"); }
-



 浙公网安备 33010602011771号
浙公网安备 33010602011771号