【做题纪要】冲刺NOIP逆天题单之动态规划篇
Game on Sum(Easy Version)
题面
Alice 和 Bob 正在玩一个游戏,游戏分为 \(n\) 个回合,Alice 和 Bob 要轮流对一个数 \(x\) 进行操作,已知这个数初始值是 \(0\)。
具体每个回合的行动规则如下:
-
Alice 选择一个在区间 \([0,k]\) 之间的实数 \(t\)。
-
Bob 可以选择让 \(x\) 变成 \(x+t\) 或者 \(x-t\),但是 Bob 在 \(n\) 个回合之内至少选择 \(m\) 次让 \(x\) 变成 \(x+t\)。
Alice想让最终的 \(x\) 最大,Bob 想让最终的 \(x\) 最小。
已知双方均采用最优策略,求最终的 \(x\) 值(对 \(10^9+7\) 取模)。
数据范围保证:\(1\le m\le n\le 2000,k\le10^9+7\)。
(题解)
逆天冲刺 NOIP 题单可做题之一。
首先看到题目是一个想让最后结果较大,一个想让最后结果较小,两者均选择最优策略,所以可以考虑 \(\text{dp}\),经典套路了。
然后设 \(f_{i,j}\) 为用掉 \(i\) 轮且使用了 \(j\) 次加法后的对应的 \(x\) 的值,可以知道 \(f_{n,m}\) 为最后的结果。
然后对于 Bob (他想要让最后结果较小) 的转移方程就很明显了。
这里\(f_{i-1,j}\)表示上一次不使用加法,\(f_{i-1,j-1}\)表示上一次使用加法(似乎很明显吧)。
而 Alice 希望这个结果最大,因此我们可知其会让 \(f_{i-1,j}-t=f_{i-1,j-1}+t\) (很明显是因为这里要取 \(\min\) )。
那么用最基本的等式的基本性质可以解一下上面那个式子去求出 \(t\) 的值。
我们解出 \(t\) 的之后可以带回原本的转移方程来求出对应的 \(f_{i,j}\) 了。
边界值\(f_{i,0}=0,f_{i,i}=i\times k\),然后直接大力 \(\text{dp}\) 即可。
这是朴素代码,复杂度是 \(\text O(Tnm)\) 无法通过此题。
点击查看代码
namespace solve{
inline int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline void write(const int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
inline void print(const int x,string s){
if(x<0) putchar('-');
write(x<0?-x:x);
int len=s.size();
for_(i,0,len-1) putchar(s[i]);
}
int f[2000][2000];
inline void In(){
const int mod=1e9+7,inv=5e8+4;
int T=read();
while(T--){
int n=read(),m=read(),k=read();
for_(i,1,n){
f[i][i]=i*k%mod;
}
for_(i,2,n){
for_(j,1,i-1){
f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod*inv%mod;
}
}
print(f[n][m],"\n");
}
}
}
那咋办呢?完全可以 \(\text O(nm)\) 预处理一遍,然后 \(\text O(1)\) 去查询。
但是这样就有个问题,原本我们是让 \(f_{i,i}=i\times k\),而现在我们需要让 \(f_{i,i}=i\),在查询 \(f_{n,m}\) 的时候乘上 \(k\) 。
复杂度 \(\text{O}(nm)\) 可以通过此题
点击查看代码
int f[3000][3000];
inline void In(){
const int mod=1e9+7,inv=5e8+4;
for_(i,1,2005){
f[i][i]=i;
}
for_(i,2,2005){
for_(j,1,i-1){
f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod*inv%mod;
}
}
int T=read();
while(T--){
int n=read(),m=read(),k=read();
print(f[n][m]*k%mod,"\n");
}
}
Hard Version 是尊贵数学,先咕了
Birds
题面
一条直线上有 \(n\) 棵树,第 \(i\) 棵树上有 \(c_i\) 只鸟。
在第 \(i\) 棵树底下召唤一只鸟的魔法代价是 \(\text{cost}_i\)。每召唤一只鸟,魔法上限会增加 \(\text B\)。从一棵树走到另一棵树,会增加魔法 \(\text X\)。一开始的魔法和魔法上限都是 \(\text W\)。
问最多能够召唤的鸟的个数。
(题解)
逆天冲刺 NOIP 题单可做题之二。
首先看数据范围,肯定不能用魔法上限和魔法做 \(\text{dp}\) 的决策。
考虑 \(f_{i,j}\) 表示在走到第 \(i\) 棵树,买了 \(j\) 只鸟的时候的最大魔力数。
-
为什么不需要记录魔力上限?
因为魔力上限为 \(\text W+i\times \text{cost}_i\),可以直接计算,不需要记录。
然后很明显的我们存在一个转移方程。
因为存在魔力上限和魔力下限,因此 \(f_{i,j}>0\) 且 \(f_{i,j}<\text W+\text{cost}_i \times j\)。
这里有一个边界,\(f_{0,0}=\text W\),因为此时没有选择任何一只鸟而且没有走任何一棵树。
最后只要倒序枚举去判断是否存在即可,这样就能求出最大的鸟数。
点击查看代码
namespace solve{
inline int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline void write(const int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
inline void print(const int x,string s){
if(x<0) putchar('-');
write(x<0?-x:x);
int len=s.size();
for_(i,0,len-1) putchar(s[i]);
}
int c[1005],C[1005],sum[1005],f[1005][10005];
inline void In(){
int n=read(),W=read(),B=read(),X=read();
for_(i,1,n){
c[i]=read();
}
for_(i,1,n){
C[i]=read();
}
for_(i,1,n){
sum[i]=sum[i-1]+c[i];
}
memset(f,-1,sizeof(f));
f[0][0]=W;
for_(i,1,n){
for_(j,0,sum[i]){
int len=min(j,c[i]);
for_(k,0,len){
if(f[i-1][j-k]-C[i]*k>=0){
if(f[i-1][j-k]!=-1){
f[i][j]=max(f[i-1][j-k]+X-C[i]*k,f[i][j]);
}
}
}
if(f[i][j]>W+B*j) f[i][j]=W+B*j;
}
}
_for(i,sum[n],1){
if(f[n][i]!=-1){
print(i,"\n");
return;
}
}
print(0,"\n");
}
}
Helping People
题面
有一个长为 \(n\) 的数列,初始时为 \(a_{1..n}\)。
给你 \(q\) 个操作,第 \(i\) 个操作将 \([l_i,r_i]\) 内的数全部加一,有 \(p_i\) 的概率被执行。保证区间不会交错,即:\(\forall i,j\in[1,q],l_i\le r_i<l_j\le r_j\) 或 \(l_i\le l_j\le r_j\le r_i\) 或 \(l_j\le r_j<l_i\le r_i\) 或 \(l_j\le l_i\le r_i\le r_j\) 。
求操作完成后数列的最大值的期望。
逆天冲刺 NOIP 题单可做题之三。
因为我脑瘫记错题面里的变量名了,下面的\(m\)其实是\(q\),但是应该不影响阅读
首先我们要知道\(\text{E}(\max\{\})\ne \max\{\text{E()}\}\),不然就会理解错题意,然后错误的像我一样感觉是数据结构题。
观察题面可以发现本题保证区间不会交错,要么包含要么不交,所以根据以往的经验我们选择直接树形 \(\text{dp}\)。
这是因为区间不交我们就可以把其建成一个树形的结构,然后来大力 \(\text{dp}\)。
首先每个区间可以建立一个树,然后如果包含起来就可以直接去合成一颗比起原来更大的树,把包含的区间变成这个区间的子树,最后我们会形成一棵森林。
对于森林我们可以建立一个\(\{1\sim n\}\)的区间,这样整个森林就可以形成单独的一颗树,从而维护,这个区间我们对其编号为\(m+1\)。
然后可以比较暴力的去想,\(f_{i,j}\) 表示节点 \(i\) 的子树(点 \(i\) 所对应的区间)在经过操作后的最大值小于等于 \(j\) 的概率。
但是我们能够发现一个性质,对于某个区间,定义 \(mx\) 为其 \(\max\),那么 \(j\in\{mx,mx+m\}\)(这里很明显是因为每次 \(mx\) 至多都只会 \(+1\) 且有且只有 \(m\) 次操作,所以 \(mx\) 的最大值就是 \(mx+m\))。
那么我们就可以改变 \(f\) 数组的定义,定义 \(f_{i,j}\) 为节点 \(i\) 的子树(点 \(i\) 所对应的区间)在经过操作后最大值小于等于 \(j+maxn_i\) 的概率(\(0\le j\le m\)),时空都优化了。
然后这很明显是非常对的,因为 \(\text P(A+B)=\text P(A)+\text P(B)\)。
再用ST表去求出最开始每个区间的 \(mx\) 就可以做出来这道题了。
最后的答案很明显是\(\text E(m+1)=\text P(m+1)\times \text{val}(m+1)=\sum\limits_{i=0}^{m}((f_{m+1,i}-f_{m+1,i-1})(i+mx_{m+1}))\)。
点击查看代码
namespace solve{
inline int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline void write(const int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
inline void print(int x,string s){
if(x<0) putchar('-');
write(x<0?-x:x);
int len=s.size();
for_(i,0,len-1) putchar(s[i]);
}
vector<int> vec[5005];
struct node{
int l,r,maxn;db p;
node(){}
node(int ll,int rr,double pp,int maxm){
l=ll,r=rr,p=pp,maxn=maxm;
}
}q[5005];
db f[5005][5005];
int n,m,fa[100005],arr[100005],ans[100005][105],maxn=-1;
inline void build(){
int t=fa[n]+1;
for_(i,1,n)
ans[i][0]=arr[i];
for_(j,1,t-1)
for_(i,1,n-(1<<j)+1)
ans[i][j]=max(ans[i][j-1],ans[i+(1<<(j-1))][j-1]);
}
inline int query(int l,int r){
return max(ans[l][fa[r-l+1]],ans[r-(1<<fa[r-l+1])+1][fa[r-l+1]]);
}
inline bool cmp(node x,node y){
if(x.l!=y.l) return x.l<y.l;
else return x.r>y.r;
}
inline void dfs(int u){
int v;
for_(i,0,(int)vec[u].size()-1){
dfs(vec[u][i]);
}
f[u][0]=1-q[u].p;
for_(i,0,(int)vec[u].size()-1){
v=vec[u][i],
f[u][0]*=f[v][q[u].maxn-q[v].maxn];
}
for_(i,1,m){
ldb p1=1,p2=1;
for_(j,0,(int)vec[u].size()-1){
v=vec[u][j];
p1*=f[v][min(i-q[v].maxn+q[u].maxn-1,m)];
p2*=f[v][min(i-q[v].maxn+q[u].maxn,m)];
}
f[u][i]=q[u].p*p1+(1-q[u].p)*p2;
}
}
inline void In(){
n=read(),m=read();
for_(i,1,n){
arr[i]=read();
maxn=max(maxn,arr[i]);
if(i!=1)
fa[i]=fa[i>>1]+1;
}
build();
for_(i,1,m){
q[i].l=read();q[i].r=read();
FastI>>q[i].p;
q[i].maxn=query(q[i].l,q[i].r);
}
q[++m]=node(1,n,0.0,query(1,n));
sort(q+1,q+1+m,cmp);
for_(i,2,m){
_for(j,i-1,1){
if(q[j].l<=q[i].l&&q[i].r<=q[j].r){
vec[j].push_back(i);
break;
}
}
}
dfs(1);
ldb sum=0;
for_(i,0,m)
sum+=((f[1][i]-(!i?0:f[1][i-1]))*(i+maxn));
printf("%.9Lf",sum);
}
}
Positions in Permutations
题面
称一个 \(1\sim n\) 的排列的完美数为有多少个 \(i\) 满足 \(|P_i-i|=1\) 。
求有多少个长度为 \(n\) 的完美数恰好为 \(m\) 的排列。答案对 \(10^9+7\) 取模。
\(1 \le n \le 1000,0 \le m \le n\)。
逆天冲刺 NOIP 题单可做题之四。
二项式反演啊。
首先惯用套路,把恰好变为至少。
设 \(f(k)\) 表示至少有 \(k\) 个位置满足条件的排列数也就是我们转化出来的东西,\(g(k)\) 表示恰好有 \(k\) 个位置满足条件的排列数也就是我们最后要求的东西。
一个很明显的关系就是\(f(k)=\sum_{i=k}^n\binom{i}{k}g(i)\)
然后二项式反演(应该都会吧) \(g(k)=\sum_{i=k}^n(-1)^{i-k}\binom{i}{k}f(i)\)
结论:除开 \(p_1\) 和 \(p_n\) 外,每个位置有且只有两个数字可选择,且相邻的奇(偶)位置可选择的数字内有\(1\)个是相同的。
那么 \(\text{dp}\) 就很显然了,设 \(f_{i,j,k}\) 表示前 \(i\) 个位置中,有 \(j\) 个位置满足要求,第 \(i\) 个位置的选择情况\(k\)(\(0\le k\le 2\),\(0\)为不选,\(p_1,p_n\) 进行特殊处理)。
易得转移方程
点击查看代码
namespace solve{
const int mod=1e9+7;
inline int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline void write(const int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
inline void print(int x,string s){
if(x<0) putchar('-');
write(x<0?-x:x);
int len=s.size();
for_(i,0,len-1) putchar(s[i]);
}
int n,k;
int fact[N],Inserve[N],final[N],f[M][M][3],ans,o[2];
inline int qpow(int a,int b){
int ans=1;
while(b){
if(b&1) ans=ans*a%mod;
a=a*a%mod;b>>=1;
}
return ans;
}
inline int Comb(int n,int m){
if(n<m) return 0;
return Inserve[m]*(fact[n]*Inserve[n-m]%mod)%mod;
}
inline void In(){
fact[0]=1;o[1]=-1;o[0]=1;
for_(i,1,N){
fact[i]=fact[i-1]*i%mod;
}
Inserve[N]=qpow(fact[N],mod-2);
_for(i,N,0){
Inserve[i-1]=Inserve[i]*i%mod;
}
n=read(),k=read();
if(n==1){
if(k==0) puts("1");
else puts("0");
return;
}
if(n==2){
if(k==1) puts("0");
else puts("1");
return;
}
f[1][0][0]=f[1][1][2]=f[2][0][0]=f[2][1][1]=f[2][1][2]=1;
for_(i,3,n){
f[i][0][0]=1;
for_(j,1,(i+1)>>1){
for_(k,0,2){
if(k==0){
f[i][j][k]=(f[i-2][j][0]+f[i-2][j][1]%mod)+f[i-2][j][2]%mod;
continue;
}
if(k==1){
f[i][j][k]=(f[i-2][j-1][1]+f[i-2][j-1][0])%mod;
continue;
}
if(i==n){
continue;
}
else f[i][j][k]=(f[i-2][j-1][2]+f[i-2][j-1][1]+f[i-2][j-1][0])%mod;
}
}
}
for_(i,n-1,n){
for_(j,0,(i+1)>>1){
f[i][j][2]=(f[i][j][0]+f[i][j][1]+f[i][j][2])%mod;
}
}
for_(i,k,n){
int tmp=0;
for_(j,0,i){
tmp=(tmp+f[n][j][2]*f[n-1][i-j][2])%mod;
}
final[i]=tmp*fact[n-i]%mod;
((ans=(ans+((o[(i-k)%2]*Comb(i,k)%mod)*final[i]%mod))%mod)+=mod)%=mod;
}
print(ans,"\n");
}
}
Tavas in Kansas
题面
- 给定一张 \(n\) 个点 \(m\) 条边的可能有自环和重边的无向连通图,每条边都有一个非负边权。
- 小 X 和小 Y 在这张图上玩一个游戏,在游戏中,第 \(i\) 个城市有一个权值 \(p_i\)。
- 一开始,小 X 在城市 \(s\) 中,小 Y 在城市 \(t\) 中,两人各有一个得分,初始为 \(0\),小 X 为先手,然后轮流进行操作。
- 当轮到某一个人时,他必须选择一个非负整数 \(x\),以选定所有与他所在的城市的最短距离不超过 \(x\) 的还未被选定过的城市,他的得分将会加上这些城市的权值。
- 另外,每个人每次必须能够至少选定一个城市。
- 当没有人可以选择时,游戏结束,得分高者获胜。
- 现在请你计算出,在两人都使用最佳策略的情况下,谁会获胜(或者判断为平局)。
- \(n \le 2 \times 10^3\),\(m \le 10^5\),\(|p_i| \le 10^9\)。
逆天冲刺 NOIP 题单可做题之五。
真可做吗?CF评分*\(2900\)。
肯定要先预处理出 \(\text{A,B}\) 两点到所有点的距离,直接离散化然后跑两遍 Dijkstra ,复杂度\(\text O(n \log n)\)
然后用经典套路维护两个人的差值
很明显由于一个人选的距离只能越来越大,所以两人最后选择的距离是有用的信息,而在此之前选择的均无用
可建出一个二维平面,根据到 \(A,B\) 两点的距离\(A_i,B_i\),把每个点表示为二维平面上的一个点 \((xA_i,xB_i)\),点权为 \(a_i\),对点数和点权分别做二维前缀和得出 \(c_{i,j}\) 和 \(s_{i,j}\)
设 \(f_{i,j,0/1}\) 表示现在轮到先手/后手操作,两人上次操作分别选择了距离\(i,j\)
转移方程为
\(s_{i+1,j+1}\)直接提出,明显可以对每一列和每一行分别开一个指针维护可转移的最小位置,并分别维护最大值/最小值便于转移
最后只要判断\(f_{0,0,0}\)的符号即可。
点击查看代码
namespace solve{
const int mod=1e9+7;
inline int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline void write(const int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
inline void print(int x,string s){
if(x<0) putchar('-');
write(x<0?-x:x);
int len=s.size();
for_(i,0,len-1) putchar(s[i]);
}
int vis[M],dis[M],div[M];
int p[M],q[M],u[M],v[M],f[M][M][2];
int n,m,A,B,a[M],tot;
int xA[M],xB[M],c[M][M],s[M][M];
int ver[N],TO[N],nxt[N],head[N];
inline void Dijkstra(int s,int* d){
priority_queue<PII,vector<PII>,greater<PII > > q;
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s]=0;
q.push(make_pair(0,s));
while(!q.empty()){
int k=q.top().second; q.pop();
if(!vis[k]){
vis[k]=1;
for(int i=head[k];i;i=nxt[i]){
if(dis[k]+ver[i]<dis[TO[i]]){
dis[TO[i]]=dis[k]+ver[i];
q.push(make_pair(dis[TO[i]],TO[i]));
}
}
}
}
for_(i,1,n)
div[i]=dis[i];
sort(div+1,div+n+1);
int qwq=unique(div+1,div+n+1)-div-1;
for_(i,1,n)
d[i]=lower_bound(div+1,div+qwq+1,dis[i])-div;
}
inline void add(int x,int y,int z){
TO[++tot]=y;
ver[tot]=z;
nxt[tot]=head[x];
head[x]=tot;
}
inline void dp(){
int i,j;
for(i=0;i<=n;++i) p[i]=q[i]=n;
memset(u,-0x3f,sizeof(u));
memset(v,0x3f,sizeof(v));
for(i=n;~i;--i){
for(j=n;~j;--j){
while(c[p[j]+1][j+1]!=c[i+1][j+1]){
u[j]=max(u[j],f[p[j]][j][1]-s[p[j]+1][j+1]);
--p[j];
}
while(c[i+1][q[i]+1]!=c[i+1][j+1]) {
v[i]=min(v[i],f[i][q[i]][0]+s[i+1][q[i]+1]);
--q[i];
}
if(p[j]!=n)
f[i][j][0]=u[j]+s[i+1][j+1];
if(q[i]!=n)
f[i][j][1]=v[i]-s[i+1][j+1];
}
}
if(!f[0][0][0]) FastO<<"Flowers";
else if(f[0][0][0]>0) FastO<<"Break a heart";
else FastO<<"Cry";
}
inline void In(){
n=read(),m=read(),A=read(),B=read();
for_(i,1,n)
a[i]=read();
for_(i,1,m){
int x=read(),y=read(),z=read();
add(x,y,z),add(y,x,z);
}
Dijkstra(A,xA);
Dijkstra(B,xB);
for_(i,1,n){
c[xA[i]][xB[i]]+=1;
s[xA[i]][xB[i]]+=a[i];
}
for(int i=n;~i;--i){
for(int j=n;~j;--j) {
c[i][j]+=c[i+1][j],s[i][j]+=s[i+1][j];
}
}
for(int i=n;~i;--i) {
for(int j=n;~j;--j){
c[i][j]+=c[i][j+1],s[i][j]+=s[i][j+1];
}
}
dp();
}
}
ZS Shuffles Cards
题面
有 \(n+m\) 张牌,其中前 \(n\) 张牌上分别标着 \(1,2,\cdots,n\) 的数字,后 \(m\) 张牌是鬼牌。现在我们打乱这些牌,然后开始抽牌游戏,每一轮你可以抽一张牌:
- 如果抽到了一张标有数字 \(x\) 的牌,就移除这张牌,并将 \(x\) 加入一个集合 \(S\) ;
- 如果抽到了鬼牌,就把移除的牌重新加入牌堆,再次打乱所有牌的顺序,重新开始抽牌。如果你抽到了鬼牌,并且集合 \(S\) 已经包括了 \([1,n]\) 中全部 \(n\) 个数,那么抽牌游戏结束。
询问抽牌游戏结束的期望轮数。
逆天冲刺 NOIP 题单可做题之六。
很明显已经开始上难度了,CF评分*3000好题。
下面的步数代表的是抽到 joker 的个数。
一眼过去应该是期望 \(\text{dp}\),首先按照题意分析。
很明显如果暴力去想是非常有难度的,至少我不会。
所以我们可以先计算每一轮抽到的期望牌数再计算抽到 joker 牌的期望。
一张数字牌在 joker 牌之前的概率很明显是 \(\frac{1}{m+1}\),那么一轮的期望牌数是 \(\frac{n}{m+1}+1\)。
定义 \(f_k\) 为还剩 \(k\) 个数没有进入集合时的期望步数,转移方程如下。
对于这个式子我们可以解方程。
边界值\(f_{0}=1\),那么很明显我们甚至不需要带入方程可以直接求得 \(f_n=1+\sum\limits_{i=1}^{m}\frac{m}{i}=1+m\sum\limits_{i=1}^{m}\frac{1}{i}\)。
最后很明显是期望轮数乘上每轮期望牌数。
代码如下
点击查看代码
namespace solve{
const int mod=998244353;
inline int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline void write(int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
inline void print(int x,string s){
if(x<0) putchar('-');
write(x<0?-x:x);
int len=s.size();
for_(i,0,len-1) putchar(s[i]);
}
int n,m,inv[N]={0,1},ans;
inline void In(){
n=read(),m=read();
for(int i=2;i<N;i++)
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
for(int i=1;i<=n;i++){
ans+=inv[i];
ans%=mod;
}
print((ans*m%mod+1)*(n*inv[m+1]%mod+1)%mod,"\n");
}
}
using namespace solve;
Bear and Cavalry
逆天冲刺 NOIP 题单可做题之七。
经过 @wang54321 的讲解我大概懂了这道题怎么写了,拜谢大佬。
首先我们考虑一个弱化版的问题,如果没有每个士兵不能骑自己的马如何解决?
很明显可以直接排序,然后用排序后的 \(w_i\) 和 \(h_i\) 相乘即可。
不能骑自己的马明显也需要排序,我们先记录每个马对应的士兵是谁,然后考虑分类讨论。
如果此时的 \(w_i\) 和 \(h_i\) 并不对应就可以直接将二者连起来

如果此时的 \(w_i\) 和 \(h_i\) 对应肯定要考虑形成这样的图形
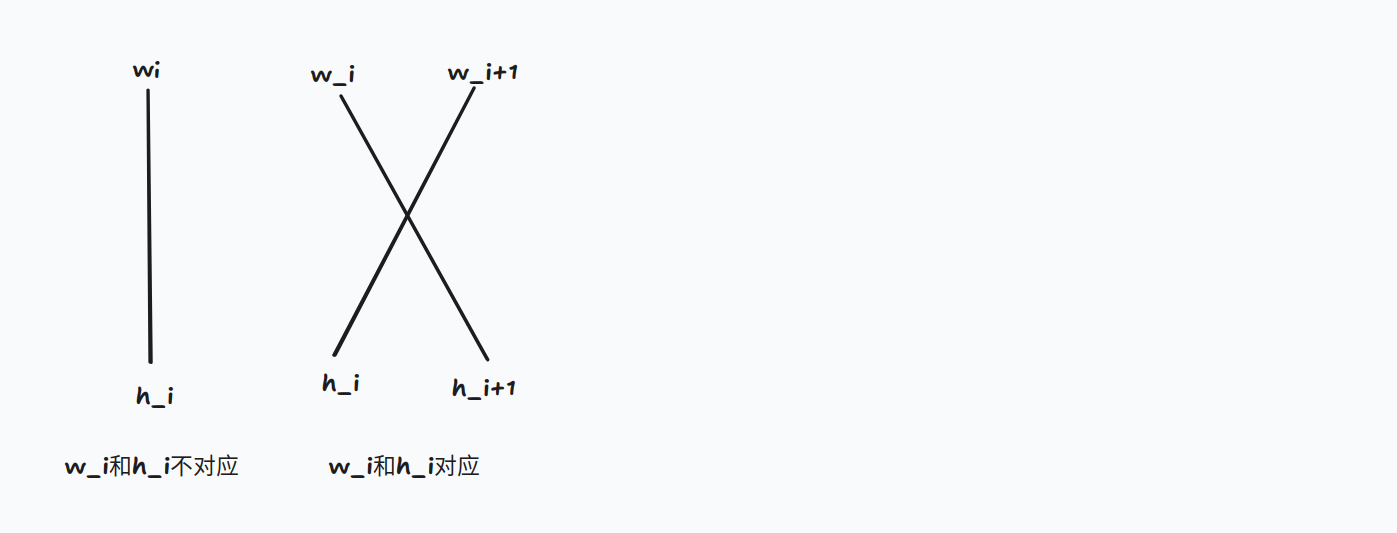
也就是让 \(w_{i}\) 和 \(h_{i+1}\) 连起来,\(w_{i+1}\) 和 \(h_i\) 连起来,可以发现这样是最优的
如果 \(w_{i}\) 和 \(h_{i}\) 对应,\(w_{i+1}\) 和 \(h_{i+1}\) 对应,\(w_{i+2}\) 和 \(h_{i+2}\) 对应(连续三个对应起来的)怎么办呢。
如果我们还是让 \(w_{i}\) 和 \(h_{i+1}\) 连起来,\(w_{i+1}\) 和 \(h_i\) 连起来,此时最后的 \(w_{i+2}\) 和 \(h_{i+2}\) 只能对应起来,那么我们就输透了。
所以我们考虑用其他方式维护,也就是形成这样的图形
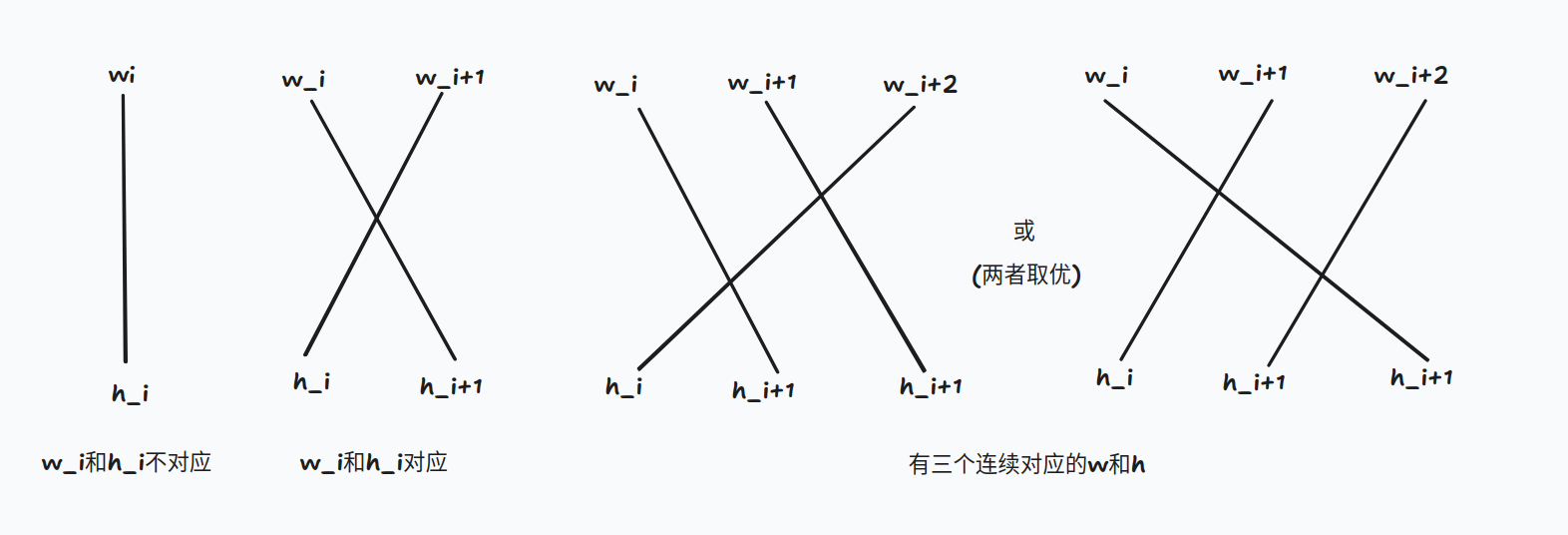
如果有超过三个呢?假设有 \(4\) 个连续对应的,我们发现可以拆成两个第二个图形。
那么我们就能发现在图中就只会存在上图内的 \(4\) 种图形,本题也就迎刃而解了。
然后设 \(f_i\) 表示前 \(i\) 个点匹配的答案,能列出 \(O(nq)\) 转移方程,卡卡常就能过。
点击查看代码
namespace solve{
inline int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline void write(const int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
inline void print(int x,string s){
if(x<0) putchar('-');
write(x<0?-x:x);
int len=s.size();
for_(i,0,len-1) putchar(s[i]);
}
struct dp{int v,id;};
inline bool cmp(dp a,dp b){return a.v<b.v;}
int posa[N],posb[N],ban[N],w1[N],w2[N],w3[N],f[N];
dp a[N],b[N];
inline void In(){
int n=read(),q=read();
for_(i,1,n){
a[i].v=read();a[i].id=i;
}
for_(i,1,n){
b[i].v=read();b[i].id=i;
}
sort(a+1,a+n+1,cmp);
sort(b+1,b+n+1,cmp);
for_(i,1,n){
posa[a[i].id]=posb[b[i].id]=i;
}
for_(i,1,n)
ban[i]=posb[a[i].id];
for_(i,1,n){
w1[i]=w2[i]=w3[i]=-INF;
int t1=-INF,t2=-INF;
if(i>=1&&ban[i]!=i)
w1[i]=a[i].v*b[i].v;
if(i>=2&&ban[i]!=i-1&&ban[i-1]!=i)
w2[i]=a[i].v*b[i-1].v+a[i-1].v*b[i].v;
if(i>=3&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
t1=a[i].v*b[i-2].v+a[i-1].v*b[i].v+a[i-2].v*b[i-1].v;
if(i>=3&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
t2=a[i].v*b[i-1].v+a[i-1].v*b[i-2].v+a[i-2].v*b[i].v;
w3[i]=max(t1, t2);
}
for_(k,0,q-1){
int x=read(),y=read();
x=posa[x],y=posa[y];
swap(ban[x],ban[y]);
int maxx=max(1,x-5),minx=min(n,x+5);
for_(i,maxx,minx) {
w1[i]=w2[i]=w3[i]=-INF;
int t1=-INF,t2=-INF;
if(i>=1&&ban[i]!=i)
w1[i]=a[i].v*b[i].v;
if(i>=2&&ban[i]!=i-1&&ban[i-1]!=i)
w2[i]=a[i].v*b[i-1].v+a[i-1].v*b[i].v;
if(i>=3&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
t1=a[i].v*b[i-2].v+a[i-1].v*b[i].v+a[i-2].v*b[i-1].v;
if(i>=3&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
t2=a[i].v*b[i-1].v+a[i-1].v*b[i-2].v+a[i-2].v*b[i].v;
w3[i]=max(t1, t2);
}
int maxy=max(1,y-5),miny=min(n,y+5);
for_(i,maxy,miny){
w1[i]=w2[i]=w3[i]=-INF;
int t1=-INF,t2=-INF;
if(i>=1&&ban[i]!=i)
w1[i]=a[i].v*b[i].v;
if(i>=2&&ban[i]!=i-1&&ban[i-1]!=i)
w2[i]=a[i].v*b[i-1].v+a[i-1].v*b[i].v;
if(i>=3&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
t1=a[i].v*b[i-2].v+a[i-1].v*b[i].v+a[i-2].v*b[i-1].v;
if(i>=3&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
t2=a[i].v*b[i-1].v+a[i-1].v*b[i-2].v+a[i-2].v*b[i].v;
w3[i]=max(t1, t2);
}
f[0]=0;
for_(i,1,n){
f[i]=f[i-1]+w1[i];
if(i>=2) f[i]=max(f[i],f[i-2]+w2[i]);
if(i>=3) f[i]=max(f[i],f[i-3]+w3[i]);
}
print(f[n],"\n");
}
}
}
Future Failure
本题是优秀结论题,没大量结论做不出来那种
首先我们要知道一个结论:\(n\&m=m\) 时组合数为奇数
分析题目,我们可以很明显的发现当先手可以选择改变先后手顺序时先手必胜,也就是当前串的排列数为偶数


