1.28闲话

喜提洛谷1天半体验卡，于今天晚上21:30过期

推歌：爱的狂想曲/洛天依 by JUSF周存

挺好听的，存娘调的好啊(赞赏

拿到手机，打开血族，发现自己还有好多抽，角色我抽到了，皮肤1000+rmb还是算了

---

今天被迫听字符串的课

为啥我这电脑没有极域啊，投屏投不到这里，重启之后依然没有，蚌埠住了

先讲了个字符串哈希

哈希的错误率很低，我们也不会用一个错误率很高的算法

😰😰😰😰😰

---

听破防了，我还是学主席树吧呃呃呃呃呃呃呃呃呃呃呃呃

\(6737151\) 年前，我们用二逼平衡树解决了查询区间第 \(k\) 小

现在我们打算用主席树去打

主席树是啥？是可持久化权值线段树

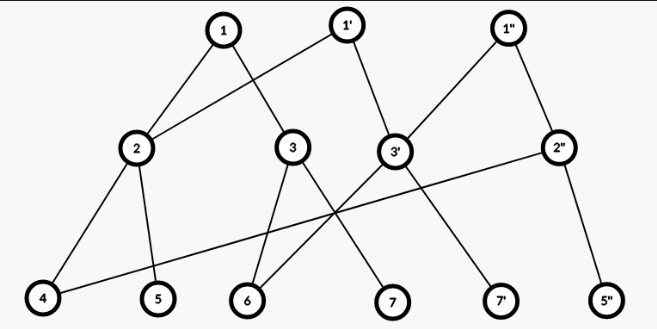
大概就是这个样子(怎么这么丑)

初始的线段树是\(1 \sim 7\)

历史版本一(就是\(1'\)开头的) 依赖初始线段树产生，内容包括 \(\{1',2,3',4,5,6,7'\}\)

历史版本二(就是\(1''\)开头的) 依赖历史版本一产生，内容包括 \(\{1'',2'',3,4,5'',6,7\}\)

我们发现每次单点修改都会创建 \(\log n\) 个新的节点

空间复杂度大致 \(O(m \log n)\)

每次新建树时依托于其修改自的版本即可

时间复杂度是尊贵的\(O(m \log n)\)

主席树 \(\ne\) 可持久化线段树

因为主席树是可持久化动态开点权值线段树

你应该(没)忘记了吧，权值线段树有个操作：查询整体第 \(k\) 小

对于查询 \([1 \sim r]\) 的区间第 \(k\) 小

我们只要通过找到插入 \(r\) 时的根节点版本，然后用普通权值线段树维护即可

如果想要查询 \([l \sim r]\) 的区间第 \(k\) 小，用\([1 \sim r]\)的信息减去\([1 \sim l-1]\)即可

---

等我把这道莫反题打出来就去打主席树的题

「Stoi2031」彩虹

目前进展

\[\begin{align}\prod_{i=1}^{r}\prod_{j=l}^{r}\text{lcm}(i,j)^{\text{lcm}(i,j)}\bmod 32465177 &=\prod_{i=1}^{r}\prod_{j=l}^{r}{(\frac{ij}{\gcd(i,j)})}^{(\frac{ij}{\gcd(i,j)})}\bmod 32465177\\ &=\prod_{d=1}^{r}\prod_{i=1}^{r}\prod_{j=l}^{r}(\frac{ij}{d})^{[\gcd(i,j)=d](\frac{ij}{d})}\bmod 32465177\\ &=\prod_{d=1}^{r}\prod_{i=1}^{\lfloor\frac rd\rfloor}\prod_{j=l}^{\lfloor\frac rd\rfloor}(ijd)^{[\gcd(i,j)=1](ijd)}\bmod 32465177\\ &=\prod_{d=1}^{r}\prod_{i=1}^{\lfloor\frac rd\rfloor}\prod_{j=l}^{\lfloor\frac rd\rfloor}(ijd)^{ijd\sum_{k|d}\mu(k)}\bmod 32465177\\ &=\prod_{d=1}^{r}\prod_{i=1}^{\lfloor\frac rd\rfloor}\prod_{j=l}^{\lfloor\frac rd\rfloor}(ijd)^{ijd\sum_{k=1}^{\lfloor\frac rd\rfloor}\mu(k)[k|i][k|j]}\bmod 32465177\\ &=\prod_{d=1}^{r}\prod_{k=1}^{r}\prod_{i=1}^{\lfloor\frac rd\rfloor}[k|i]\prod_{j=l}^{\lfloor\frac rd\rfloor}[k|j](ijd)^{ijd\times \mu(k)}\bmod 32465177\\ \end{align} \]

现在我不会了，去看了一眼题解

\[\prod_{d=1}^{r}\prod_{k=1}^{r}\prod_{i=1}^{\lfloor\frac rd\rfloor}[k|i]\prod_{j=l}^{\lfloor\frac rd\rfloor}[k|j](ijd)^{ijd\times \mu(k)}\bmod 32465177 = \prod_{d=1}^{r}\prod_{k=1}^{r}\prod_{i=1}^{\lfloor\frac r{dk}\rfloor}\prod_{j=l}^{\lfloor\frac r{dk}\rfloor}(ijdk^2)^{ijdk^2\times \mu(k)}\bmod 32465177 \]

这里是为啥啊，好像也没啥讲的比较明白的题解

正好 \(jijidawang\) 来了，直接一眼秒杀了上面那一串

这里就是相当于枚举一个新的 \(i'\) 和 \(j'\) 让 \(i'= i\times k,j'=j \times k\)，这回看懂了

\[\prod_{d=1}^{r}\prod_{k=1}^{r}\prod_{i=1}^{\lfloor\frac r{dk}\rfloor}\prod_{j=l}^{\lfloor\frac r{dk}\rfloor}(ijdk^2)^{ijdk^2\times \mu(k)}\bmod 32465177 \]

对于这一串怎么处理，我觉得其实可以提出一个\(t=dk\)

\[\prod_{t=1}^{r}\prod_{k|t}^{}\prod_{i=1}^{\lfloor\frac r{t}\rfloor}\prod_{j=l}^{\lfloor\frac r{t}\rfloor}(ijt\lfloor\frac{t}{k}\rfloor)^{ijt\lfloor\frac{t}{k}\rfloor\mu(k)}\bmod 32465177 \]

然后呢？没然后了，不会推了，换换脑子明天再推

• update:洛谷封了，写不了这道题了aaaaaaaaaaaaaaaaaaa

---

回顾一下之前打的主席树

P3919 【模板】可持久化线段树 1（可持久化数组）

思路非常简单

因为主席树会有多个根节点，每个节点不一定只有一个父节点，每个根节点都能组成一颗完整的线段树

那么我们可以保存大量根节点，借此就能建立多个历史版本

写了份代码

#include<bits/stdc++.h>
#define int long long
#define lc ls[m]
#define rc rs[m]
using namespace std;
const int N=0x66CCFF*5;
int a[N],n,q,rt[N];
int ls[N],rs[N],val[N],ans,m,v;
inline int read(){
    int f=1,x=0;char ch;
    while(ch<'0'||ch>'9'){ch=getchar();if(ch=='-')f=-1;};
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();};
    return f*x;
}
inline void build(int &q,int l,int r){
    q=++ans;
    if(l==r){val[q]=a[l];return;}
    int mid=(l+r)>>1;
    build(ls[q],l,mid);
    build(rs[q],mid+1,r);
}
inline void change(int &m,int tot,int l,int r,int q,int v){
    m=++ans;
    lc=ls[tot];rc=rs[tot];
    val[m]=val[tot];
    if(l==r){val[m]=v;return;}
    int mid=(l+r)>>1;
    if(q<=mid) change(lc,ls[tot],l,mid,q,v);
    else change(rc,rs[tot],mid+1,r,q,v);
}
inline int ask(int m,int l,int r,int q){
    if(l==r)
        return val[m];
    int mid=(l+r)>>1;
    if(q<=mid)
        return ask(lc,l,mid,q);
    else 
        return ask(rc,mid+1,r,q);
}
signed main(){
    // freopen("1.in","r",stdin);
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        a[i]=read();
    build(rt[0],1,n);
    for(int i=1;i<=m;i++){
        int tot=read(),opt=read(),x=read();
        if(opt==1)
			v=read();
			change(rt[i],rt[tot],1,n,x,v);
        if(opt==2){
			cout<<ask(rt[tot],1,n,x)<<"\n";
			rt[i]=rt[tot];
		}
    }
}