splay学习笔记

二叉搜索树

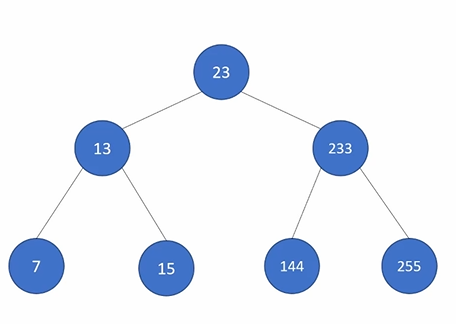
定义以下变量

• $fa[x] $

  \(x\)的父亲节点

• \(son[x][0/1]\)

  \(x\)的左/右儿子

• \(key[x]\)

  \(x\)的键值，按照键值维护节点的位置

• \(sz[x]\)

  \(x\)的子树大小

五种操作:

• insert操作

  操作含义：将一个点插入

  先令\(now=root\)

  如果\(key[now]>k\)(要插入的点的\(key\))就向左走，否则向右走

  如果已经到最底下了就可以直接插入，整棵树的大小\(+1\)，新节点的左右儿子(虽然是空的)父亲还有各项之要一一对应最后做一下它父亲的\(pushup\)

• rk操作

  寻找第\(x\)的节点的排名

  初始化\(now=root,ret=1\)

  如果当前点的\(key\le x\)，应该向左儿子走

  否则向右儿子走，此时\(ret+=\)左儿子大小\(+1\)

  最后\(pushdown\)

• kth操作

  寻找排名为k的点

  初始化now=root

  如果当前点有左子树且k比左子树的大小小则向左子树寻找

  否则向右寻找k-=左子树大小+1

  \(pushdown\)

• 求前驱/后继

  前驱:第一个小于\(x\)的数

  后继:第一个大于\(x\)的数

  对于前驱首先令tmp=root,ret=-inf如果key[tmp]< x 则 ret=max(ret,key[tmp])接着向右走

  对于后继和前驱同理不过方向相反

  如果需要更改要记得\(pushdown\)

• \(del\)操作

  现在要删除值为\(x\)的点整体思路就是用某个点把它挤掉

  先找到\(x\)在树中的编号

  为了方便删除我们希望放到一个只有一个儿子或没有儿子的位置上

  如果当前点同时有左右儿子就先找到它的前驱用前驱替换掉它

  现在删掉的点一定只有一个儿子或没有儿子，删除后直接把儿子接到父亲上就行

  在最后要一路pushup上去还要看一下整棵树的root有没有改变

二叉查找树自然是有很大缺陷的不然就不学平衡树了

二叉搜索树的缺陷就是毒瘤出题人可能会用一条链来卡你，这是非常讨厌了

平衡树

• 定义

  平衡二叉树具有以下性质：她是一颗空树或者她的左右两个子树的高度差的绝对值不超过\(1\)而且左右两个子树都是一颗平衡二叉树

  

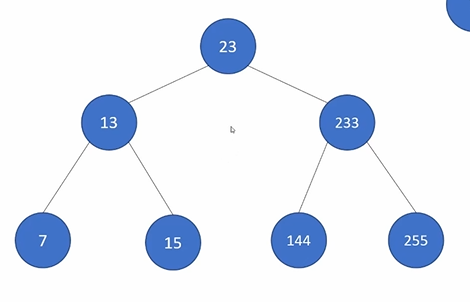
  这就是一颗平衡树

  那么平衡树怎么实现呢?

  

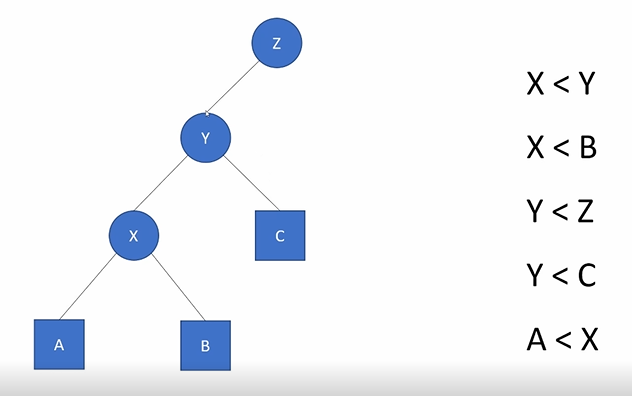
  这里的圆是一个节点而方块是一个子树

  splay有一个基本操作：旋转

  对于上面的平衡树，可以旋转为

  

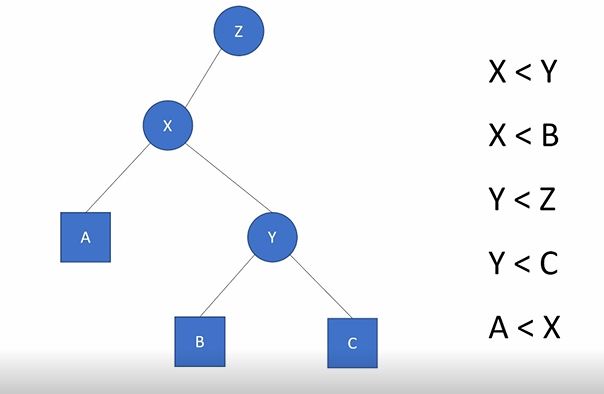
  那么是怎么实现的呢？

  • rotate操作

    在splay中有几种基本的旋转用于实现平衡：左旋和右旋

    我们可以认为3个点中有以下四种，且旋转节点都为\(x\)

    

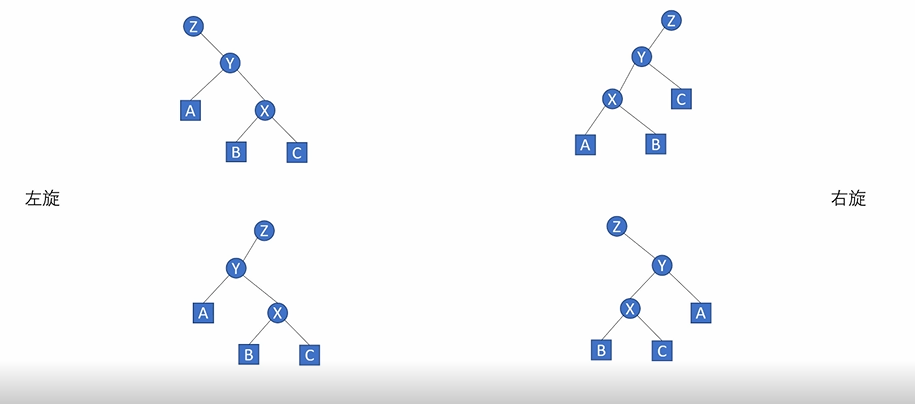
    进行左旋和右旋后的结果如下

    

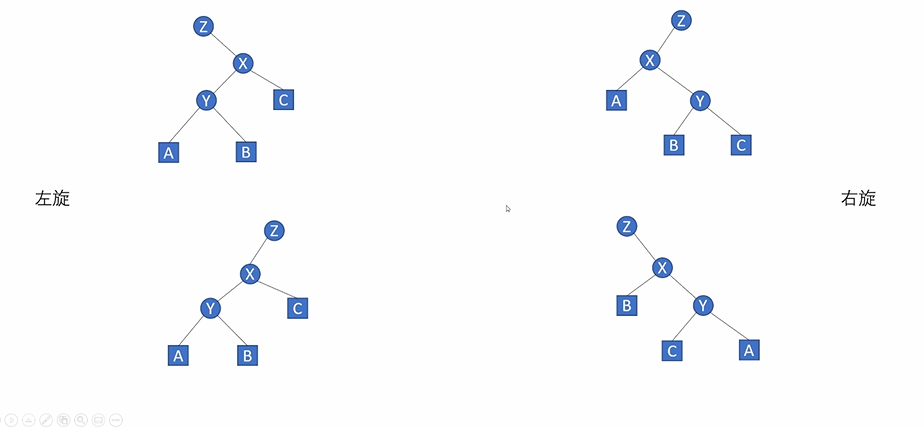
    旋转的代码非常简单

    inline void rotate(int x){
        int old=f[x],oldf=f[old],which=get(x);
        ch[old][which]=ch[x][which^1];
        f[ch[old][which]]=old;
        ch[x][which^1]=old;
        f[old]=x;
        f[x]=oldf;
        if(oldf)
            ch[oldf][ch[oldf][1]==old]=x;
        update(old);
        update(x);
        return;
    }
    

    这里的get用途是判断x是左儿子还是右儿子

    inline int get(int x){
        return ch[f[x]][1]==x;
    }
    

    而update是用于更新节点的值

    inline void update(int x){
        if(x){
            siz[x]=cnt[x];
            if(ch[x][0])
                siz[x]+=siz[ch[x][0]];
            if(ch[x][1])
                siz[x]+=siz[ch[x][1]];
        }
    }
    

    无论是左旋还是右旋都可以通过上面的rotate函数来实现

  • splay操作

    把某个点rotate到我们需要的位置

    其实splay是rotate的发展，只是在不停的rotate直到达到目标状态

    过程中需要分类讨论

    • 如果三点一线则需要先rotate掉x的父亲再rotate(x)

    • 否则直接rotate(x)

    这里的splay是直接rotate到根节点

    inline void splay(int x){
        for(int fa;fa=f[x];rotate(x))
            if(f[fa])
                rotate(get(x)==get(fa)? fa : x);
            root=x;
    }
    

  • insert操作

    相对简单，只要在正常的insert操作基础上splay防止失衡即可

    inline void insert(int v){
        if(root==0){
            root=++sz;
            ch[root][0]=ch[root][1]=f[root]=0;
            key[root]=v;
            cnt[root]=siz[root]=1;
            return;
        }
        int cur=root,fa=0;
        while(1){
            if(key[cur]==v){
                ++cnt[cur];
                update(cur);
                update(fa);
                splay(cur);
                break;
            }
            fa=cur;
            cur=ch[cur][key[cur]<v];
            if(cur==0){
                ch[++sz][0]=ch[sz][1]=0;
                key[sz]=v;
                siz[sz]=1;
                cnt[sz]=1;
                f[sz]=fa;
                ch[fa][key[fa]<v]=sz;
                update(fa);
                splay(sz);
                break;
            }
        }
    }
    

  • pre/nxt

    找前驱后继，直接根据定义在平衡树上找就行

    inline int pre(){
        int cur=ch[root][0];
        while(ch[cur][1])
            cur=ch[cur][1];
        return cur;
    }
    inline int nxt(){
        int cur=ch[root][1];
        while(ch[cur][0])
            cur=ch[cur][0];
        return cur;
    }
    

  • del操作

    单点删除

    先find一下v(查询v的排名)，然后把它splay到根

    分成多种情况讨论：

    1.t[root].cnt>1:不只有一个要删除的节点，直接 −1 即可

    2.root只有一个同时没有子节点：直接clear

    3.若root只有左儿子或右儿子：删除root，唯一的儿子做root

    4.root有两个儿子：用root的前驱做新的root，把原root的右子树接到新的root右子树上（前root一定无左子树）

    删完要update

    inline void del(int v){
        find(v);
        if(cnt[root]>1){
            --cnt[root];
            update(root);
            return;
        }
        if(!ch[root][0] && !ch[root][1]){
            clear(root);
            root=0;
            sz=0;
            return;
        }
        if(!ch[root][0]){
            int oldroot=root;
            root=ch[root][1];
            f[root]=0;
            clear(oldroot);
            --sz;
            return;
        }
        else if(!ch[root][1]){
            int oldroot=root;
            root=ch[root][0];
            f[root]=0;
            clear(oldroot);
            --sz;
            return;
        }
        int lpre=pre(),oldroot=root;
        splay(lpre);
        f[ch[oldroot][1]]=root;
        ch[root][1]=ch[oldroot][1];
        update(root);
        return;
    }
    

    splay支持区间删除

    如果我们要删除排名\([l\sim r]\)的点，我们只需要找到\(l-1\)并且旋转到根然后找到\(r+1\)旋转到根的下面

    这样就可以推出root=l-1，且son[root][1]=r+1

    然后以son[son[root][1]][0]为根的这颗子树一定是那段区间，接下来直接把它和主树的联系断开就行，然后update它的父亲和父亲的父亲

    • reserve翻转操作

    splay支持区间翻转操作

    如果要翻转排名为\([l,r]\)的点，类似删除先提取出这一区间

    先对当前节点打上翻转标记，表示它的左右儿子等待应用翻转操作

    接下来当该点的tag==1时交换其左右儿子并下传tag标记

    为了方便处理边界我们选择插入边界节点-INF和INF

    
    inline void turn( int l , int r ) {
        l=findth(l);
        r=findth(r+2);
        splay(l,0);
        splay(r,l);
        pushdown(root);
        tag[ch[ch[root][1]][0]]^=1;
    }
    
    

    注意在此时支持reserve的splay旋转需要有目标了

    但是其实还是非常简单

    inline void splay(int x,int goal){
        for(int fa;(fa=f[x])!=goal;rotate(x)){
            if(f[fa]!=goal){
                rotate((get(x)==get(fa)?fa:x));
            }
        }
        if(!goal){
            root=x;
        }
        return;
    }
    

    推平标记就是一个lazy函数

    inline void lazy(int x){
        if(x&&tag[x]){
            tag[ch[x][0]]^=1;
            tag[ch[x][1]]^=1;
            swap(ch[x][0],ch[x][1]);
            tag[x]=0;
        }
    } 
    

  接下来基本的splay操作就介绍完了

• 例题

  • 普通平衡树
  $My\ Code$

  #include<bits/stdc++.h>
  using namespace std;
  #define int long long
  const int N=100005,INF=0x3f3f3f3f3f;
  int t,opt;
  int f[N],ch[N][2],key[N],cnt[N],siz[N],sz,root;
  inline void clear(int x)
  {
      ch[x][0]=ch[x][1]=f[x]=cnt[x]=key[x]=siz[x]=0; 
  }
  inline int get(int x)
  {
      return ch[f[x]][1]==x;
  }
  inline void update(int x)
  {
      if(x)
      {
          siz[x]=cnt[x];
          if(ch[x][0])
          {
              siz[x]+=siz[ch[x][0]];
          }
          if(ch[x][1])
          {
              siz[x]+=siz[ch[x][1]];
          }
      }
      
  }
  inline void rotate(int x)
  {
      int old=f[x],oldf=f[old],which=get(x);
      ch[old][which]=ch[x][which^1];
      f[ch[old][which]]=old;
      ch[x][which^1]=old;
      f[old]=x;
      f[x]=oldf;
      if(oldf)
          ch[oldf][ch[oldf][1]==old]=x;
      update(old);
      update(x);
      return;
  }
  inline void splay(int x)
  {
      for(int fa;fa=f[x];rotate(x))
          if(f[fa])
              rotate(get(x)==get(fa)? fa : x);
          root=x;
  }
  inline void insert(int v)
  {
      if(root==0)
      {
          ++sz;
          root=sz;
          ch[root][0]=ch[root][1]=f[root]=0;
          key[root]=v;
          cnt[root]=siz[root]=1;
          return;
      }
      int cur=root,fa=0;
      while(1)
      {
          if(key[cur]==v)
          {
              ++cnt[cur];
              update(cur);
              update(fa);
              splay(cur);
              break;
          }
          fa=cur;
          cur=ch[cur][key[cur]<v];
          if(cur==0)
          {
              ++sz;
              ch[sz][0]=ch[sz][1]=0;
              key[sz]=v;
              siz[sz]=1;
              cnt[sz]=1;
              f[sz]=fa;
              ch[fa][key[fa]<v]=sz;
              update(fa);
              splay(sz);
              break;
          }
      }
  }
  inline int find(int v)
  {
      int ans=0,cur=root;
      while(1)
      {
          if(v<key[cur])
              cur=ch[cur][0];
          else 
          {
              ans+=(ch[cur][0] ? siz[ch[cur][0]] : 0);
              if(v==key[cur])
              {
                  splay(cur);
                  return ans+1;
              }
              ans+=cnt[cur];
              cur=ch[cur][1];
          }
      }
  }
  inline int findth(int k)
  {
      int cur=root;
      while(1)
      {
          if(ch[cur][0] && k<=siz[ch[cur][0]])
              cur=ch[cur][0];
          else {
              int tem=(ch[cur][0] ? siz[ch[cur][0]] : 0) +cnt[cur];
              if(k<=tem)
                  return key[cur];
              k-=tem;
              cur=ch[cur][1];
          }
      }
  }
  inline int pre()
  {
      int cur=ch[root][0];
      while(ch[cur][1])
          cur=ch[cur][1];
      return cur;
  }
  inline int nxt()
  {
      int cur=ch[root][1];
      while(ch[cur][0])
          cur=ch[cur][0];
      return cur;
  }
  inline void del(int v)
  {
      find(v);
      if(cnt[root]>1)
      {
          --cnt[root];
          update(root);
          return;
      }
      if(!ch[root][0] && !ch[root][1])
      {
          clear(root);
          root=0;
          sz=0;
          return;
      }
      if(!ch[root][0])
      {
          int oldroot=root;
          root=ch[root][1];
          f[root]=0;
          clear(oldroot);
          --sz;
          return;
      }
      else if(!ch[root][1])
      {
          int oldroot=root;
          root=ch[root][0];
          f[root]=0;
          clear(oldroot);
          --sz;
          return;
      }
      int lpre=pre(),oldroot=root;
      splay(lpre);
      f[ch[oldroot][1]]=root;
      ch[root][1]=ch[oldroot][1];
      update(root);
      return;
  }
  signed main()
  {
      cin>>t;
      int x;
      insert(INF);
      insert(-INF);
      while(t--)
      {
          cin>>opt;
          switch(opt)
          {
              case 1:
              {
                  cin>>x;
                  insert(x);
                  break;
              }
              case 2:
              {
                  cin>>x;
                  del(x);
                  break;
              }
              case 3:
              {
                  cin>>x;
                  insert(x);
                  cout<<find(x)-1<<endl;
                  del(x);
                  break;
              }
              case 4:
              {
                  cin>>x;
                  cout<<findth(x+1)<<endl;
                  break;
              }
              case 5:{
                  cin>>x;
                  insert(x);
                  cout<<key[pre()]<<endl;
                  del(x);
                  break; 
              }
              case 6:
              {
                  cin>>x;
                  insert(x);
                  cout<<key[nxt()]<<endl;
                  del(x);
                  break;
              }
          }
      }
  }
  

  • 文艺平衡树
  $My\ Code$

  #include<bits/stdc++.h>
  #define int long long
  #define ll long long
  #define N 100005
  using namespace std;
  int n , m;
  int num[N];
  int inf=0x66ccff0712;
  int sz=0,root=0;
  int ch[N][2],f[N],cnt[N] , key[N] , siz[N] , tag[N] , pos[N];
  inline int get(int x){
      return ch[f[x]][1]==x;
  }
  inline void update(int x) {
      if(x){
          siz[x]=cnt[x];
          if(ch[x][0])
              siz[x]+=siz[ch[x][0]];
          if(ch[x][1])
              siz[x]+=siz[ch[x][1]];
      }
  }
  inline void pushdown( int x ) {
      if(x&&tag[x]) {
          tag[ch[x][0]]^=1;
          tag[ch[x][1]]^=1;
          swap(ch[x][0],ch[x][1]);
          tag[x]=0;
      }
  }
  inline void rotate(int x){
      int old=f[x],oldf=f[old],which=get(x);
      pushdown(old);
      pushdown(x);
      ch[old][which]=ch[x][which ^ 1];
      f[ch[old][which]]=old;
      ch[x][which^1]=old;
      f[old]=x;
      f[x]=oldf;
      if(oldf) {
          ch[oldf][ch[oldf][1] == old] = x;
      }
      update( old );
      update( x );
      return; 
  }
  inline void splay(int x,int goal){
      for (int fa;(fa=f[x])!=goal;rotate(x)) 
          if( f[fa] != goal ) 
              rotate(( get(x)==get(fa) ? fa : x ));
      if(!goal)
          root=x;
      return;
  }
  inline int findth(int k) {
      int cur=root;
      while(true){
          pushdown(cur);
          if(ch[cur][0] && k <= siz[ch[cur][0]])
              cur=ch[cur][0];
          else{
              int tem=(ch[cur][0]?siz[ch[cur][0]]:0)+cnt[cur];
              if( k<=tem)
                  return cur;
              k-=tem;
              cur=ch[cur][1];
          }
      }
  }
  inline int build( int p , int l , int r ) {
      if(l>r)
          return 0;
      int mid=(l+r)>>1;
      int cur=++sz;
      key[cur]=pos[mid];
      f[cur]=p;
      tag[cur]=0;
      siz[cur]++;
      cnt[cur]++;
      ch[cur][0]=build(cur,l,mid-1);
      ch[cur][1]=build(cur,mid+1,r);
      update(cur);
      return cur;
  }
  inline void turn( int l , int r ) {
      l=findth(l);
      r=findth(r+2);
      splay(l,0);
      splay(r,l);
      pushdown(root);
      tag[ch[ch[root][1]][0]]^=1;
  }
  void write(int cur){
      pushdown(cur);
      if(ch[cur][0])
          write(ch[cur][0]);
      if( key[cur]!=-inf&&key[cur]!=inf)
          cout<<num[key[cur]]<<" ";
      if(key[ch[cur][1]])
          write(ch[cur][1]);
  }
  signed main() {
      cin>>n>>m;
      for(int i=1;i<=n;++i){
          num[i]=i;
          pos[i+1]=i;
      }
      pos[1]=-inf;
      pos[n+2]=inf;
      root=build(0,1,n+2);
      for (int i=1;i<=m;++i){
          int x,y;
          cin>>x>>y;
          turn(x,y);
      }
      write(root);
  }