AC自动机学习笔记
什么是自动机
一般指确定有限状态自动机，所以AC自动机不是自动AC机
自动机是一个非常广泛使用的数学模型
-
自动机是一个对信号序列进行判定的模型
解释一下上面那句话
信号序列是指一串有顺序的信号例如字符串的从前到后每一个字符
判定是指对某一个命题给出真或者假的判断
对于自动机，一共存在3种信号序列
-
不能识别
-
判定结果为真
-
判定结果为假
-
-
自动机的结构其实是一张有向图
其中自动机每个节点都是一个判定节点，节点只是状态而非任务，边可以接受多种字符
下面的是一个判断一个二进制数是不是偶数的自动机
从起始结点开始，从高位到低位接受这个数的二进制序列，看最终停在哪里。
若最终停在红圈结点，则是偶数，否则则反之
-
自动机只是数学模型，不是算法，不是数据结构
因此用不同的实现方法可以得到不同的复杂度
形式化定义
一个\(\text{DFA}\)(确定有限状态自动机,即自动机)由五部分组成
-
字符集\(\sum\) :
本自动机只能输入这些字符
-
状态集合\(Q\) :
如果把一个\(\text{DFA}\)看成有向图则\(\text{DFA}\)中的状态就相当于图上的顶点
-
起始状态\(s\) :
对于\(s\in Q\)，\(s\)是一个特殊的状态
-
接受状态集合\(F\) :
对于\(F\subseteq Q\),\(F\)是一组特殊状态
-
转移函数\(\delta\) :
\(\delta\) 是一个接受两个参数返回一个值的函数，其中第一个参数和返回值都是一个状态而第二个参数是字符集\(\sum\)中的一个字符
把一个\(\text{DFA}\)看成一张有向图，\(\text{DFA}\)中的\(\delta\)就相当于边，每条边上都有一个字符
\(\text{DFA}\)的作用是识别字符串，对于自动机 \(\text A\) ，若它能识别字符串 \(S\) ，那么 \(A(S)=\mathrm{T}\) ，反之\(A(S)=\mathrm{F}\) 。
当 \(DFA\) 读入一个字符串时，从初始状态起按照转移函数一个一个字符地转移。
如果读入完一个字符串的所有字符后位于一个接受状态，那么称 \(DFA\) 接受 这个字符串，反之称 \(DFA\) 不接受 这个字符串。
如状态 \(v\) 没有字符 \(c\) 的转移，则令 \(\delta(v,c)=\mathrm{null}\) ，而 \(\mathrm{null}\) 只能转移到 \(\mathrm{null}\) ，且 \(\mathrm{null}\) 不属于接受状态集合。
无法转移到接受状态的状态可以视作 \(\mathrm{null}\) ，也可以说 \(\mathrm{null}\) 代指所有无法转移到接受状态的状态
我们扩展定义转移函数 [\delta] ，令其第二个参数可以接收一个字符串： [\delta(v,s)=\delta(\delta(v,s[1]),s[2..|s|])] ，扩展后的转移函数就可以表示从一个状态起接收一个字符串后转移到的状态。那么， [A(s)=[\delta(start,s)\in F]] 。
下图是一个接受且仅接受字符串 "\(a\)", "\(ab\)", "\(aac\)" 的 \(\text{DFA}\)：
\(\text{AC}\)自动机
AC自动机是以Trie为基础结合KMP的思想建立的自动机
KMP算法是求单字符串对单字符串的匹配使用的,而AC自动机是求多个字符串在一个字符串上的匹配使用的
AC自动机的实现
AC自动机需要提前知道所有的需要匹配的字符串
-
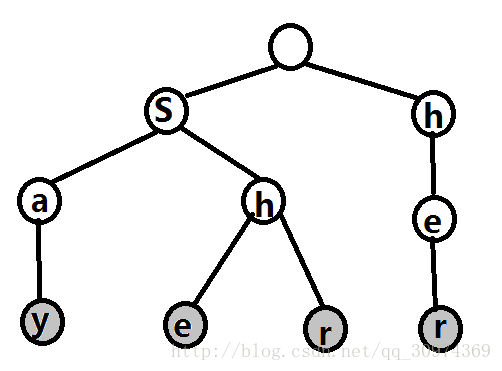
第一步 把需要匹配的字符串构建成一棵Trie树
-
第二步 对Trie树上的所有节点构造失配指针
构建Trie树
普通的Trie，该怎么建就怎么建
这里借用大佬的图片
构建失配指针
\(fail\)指针在这里的作用是每次沿着Trie树匹配，当前位置没有匹配上时，直接跳转到失配指针所指向的位置继续进行匹配
在这里\(fail\)指针指向的是一个在\(\text{Trie}\)里存在的最长的与真后缀相同的字符串。
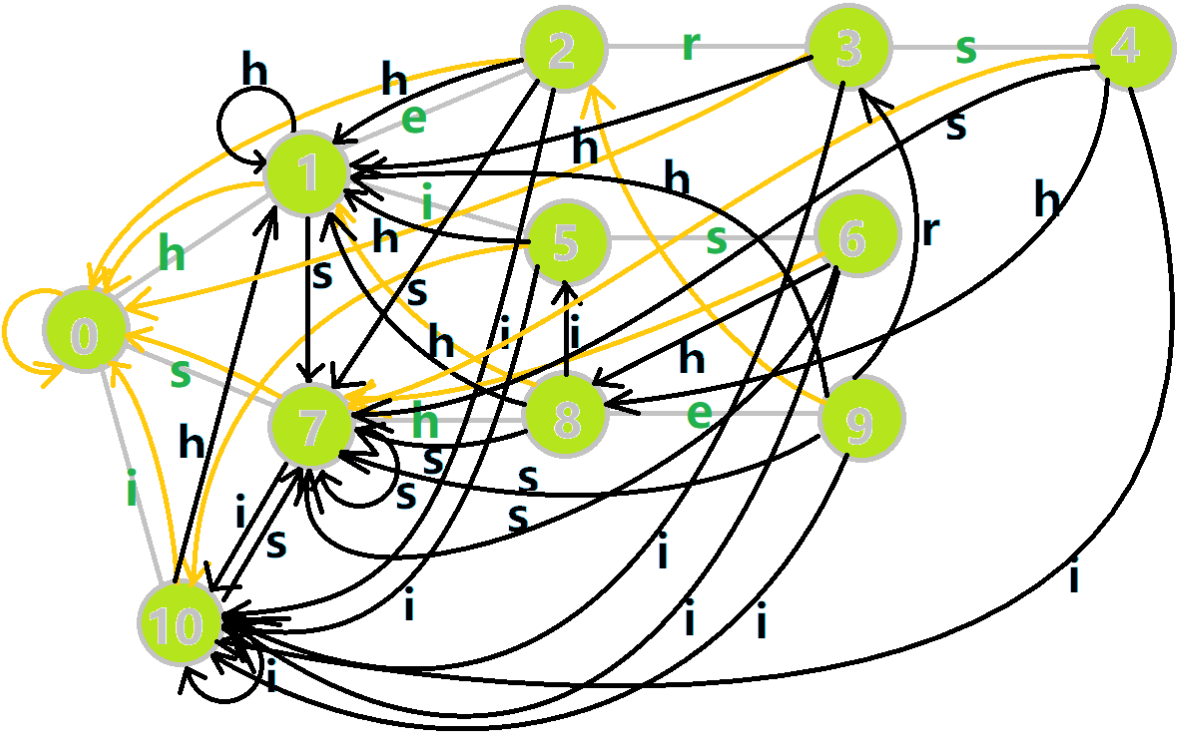
用OI-wiki的图举个例子
如 \(she\)，她的真后缀有 \(he\)，\(e\) 和 \(\varnothing\)，其中 \(he\) 和 \(\varnothing\) 存在于 \(\text{Trie}\) 树中，则让 \(9\) 号节点的 \(fail\) 指针指向最长的 \(he\) 的末尾节点 \(2\) 号节点
如 \(her\)，她的真后缀有 \(er\)，\(r\) 和 \(\varnothing\)，只有 \(\varnothing\) 存在于 Trie 树中，则让 \(3\) 号节点的 \(fail\) 指针指向根节点 \(0\)
如何求出失配指针
当前节点 \(p\) 代表的字符是 \(c\)，\(p\) 的 \(fail\) 指针应指向 \(p\) 的父亲的 \(fail\) 指针的代表 \(c\) 的儿子
如图，\(9\) 代表的字符是 \(e\)，\(9\) 的父亲是 \(8\)，\(8\) 的 \(fail\) 指针指向 \(1\)，\(1\) 的代表 \(e\) 的儿子是 \(2\)，因此 \(9\) 的 \(fail\) 指针指向 \(2\) 号节点。
如果\(p\)不存在代表\(c\)的儿子则让\(c\)的\(fail\)指针指向\(p\)的\(fail\)指针指向的节点\(p'\)的代表\(c\)的儿子
如OI-wiki上的图
这里是OI-wiki上的完整动图
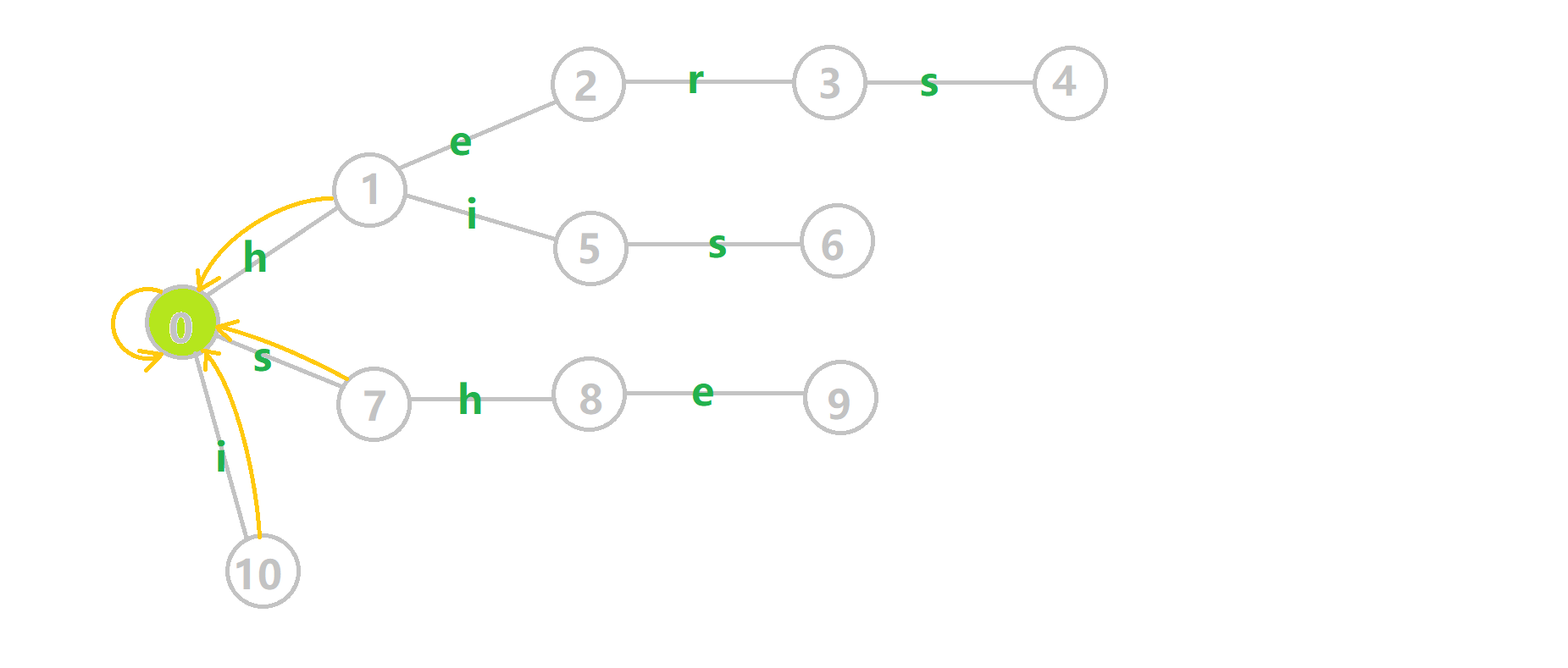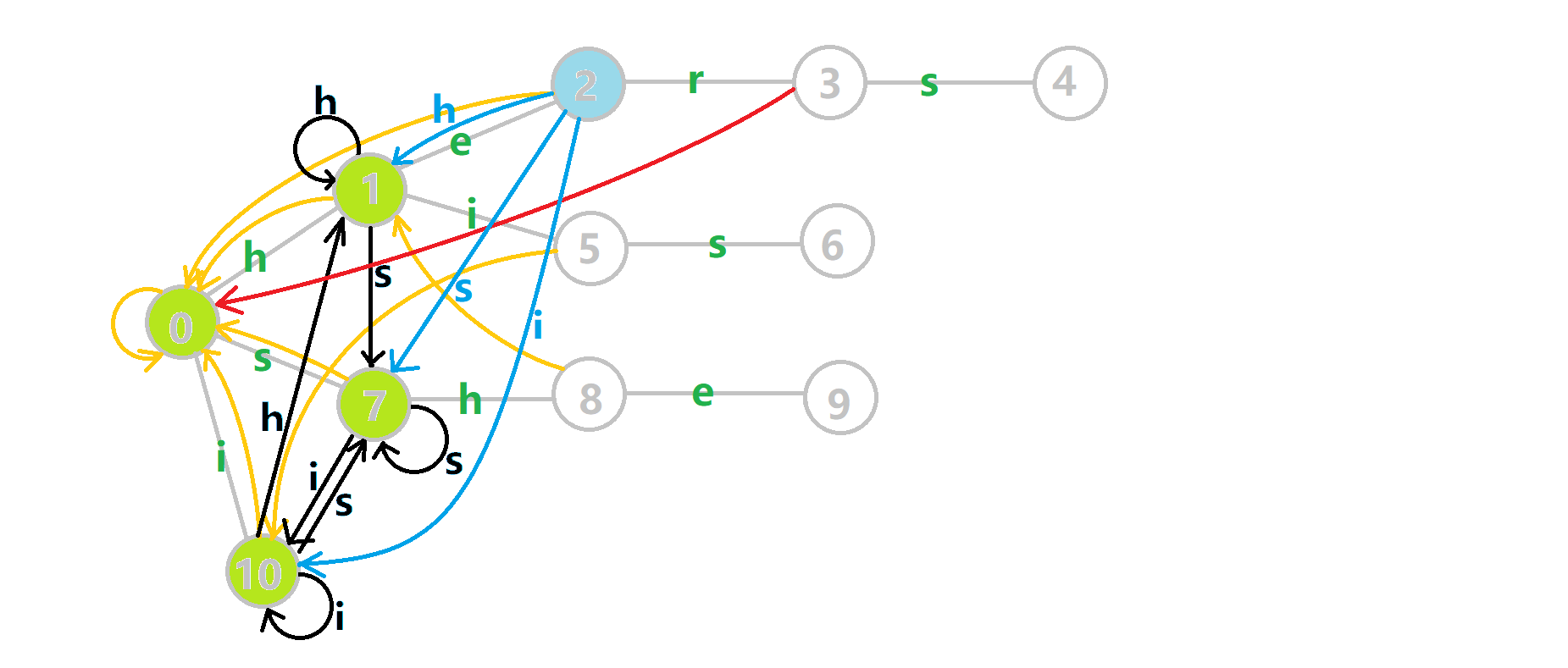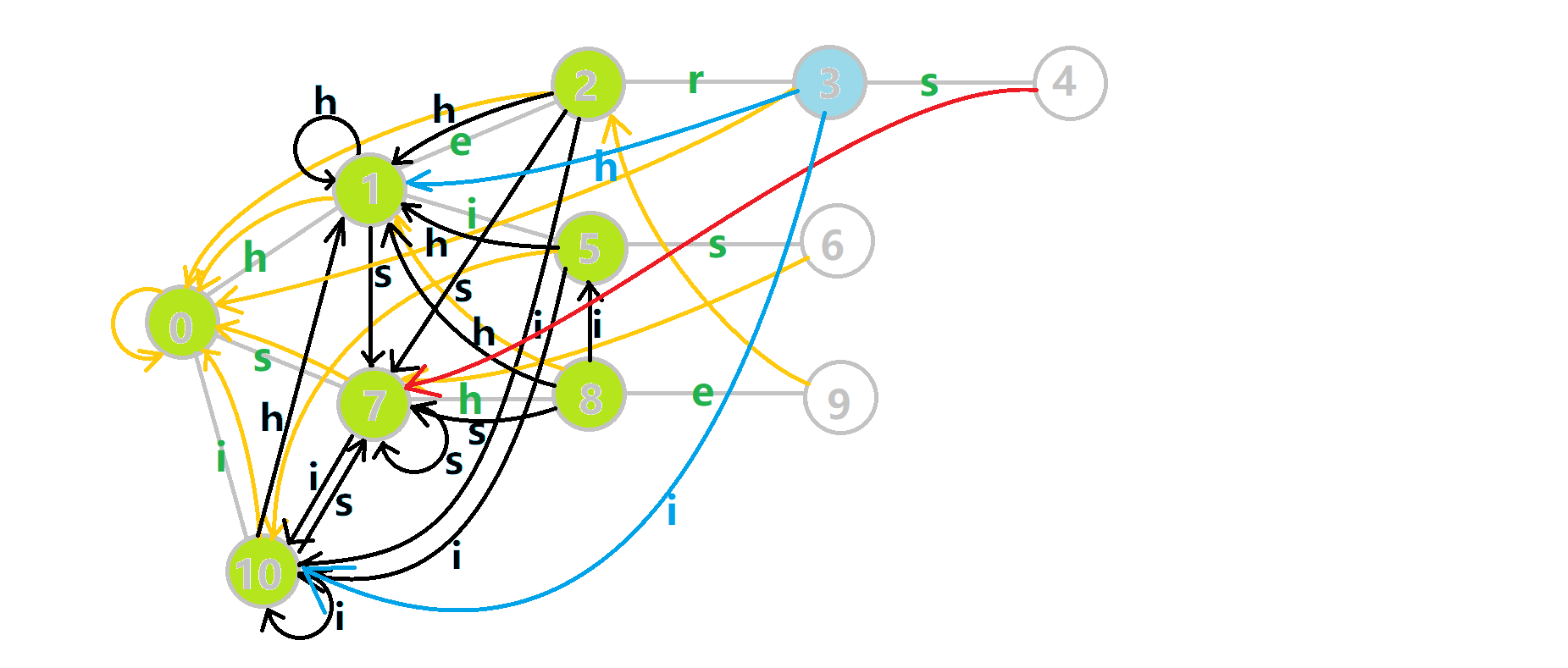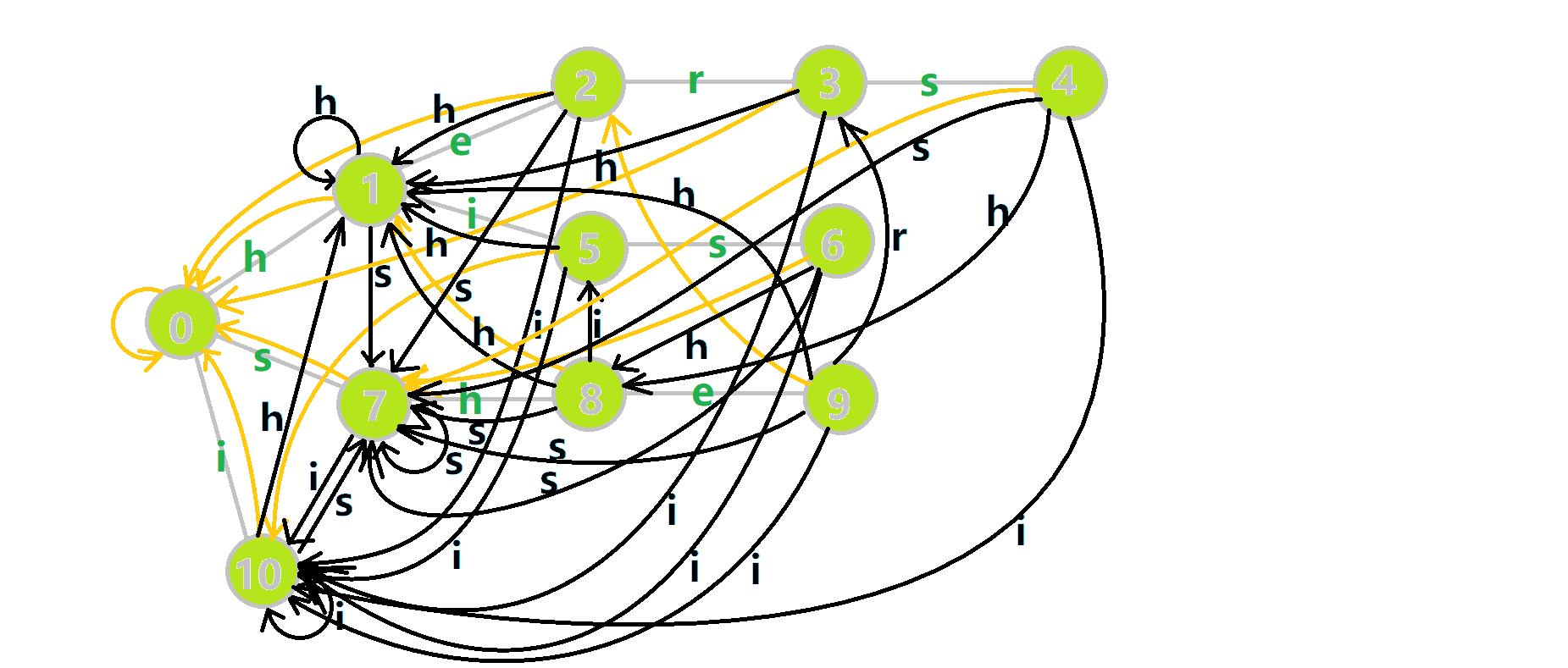
- 蓝色结点：BFS 遍历到的结点 u
- 蓝色的边：当前结点下，AC 自动机修改字典树结构连出的边。
- 黑色的边：AC 自动机修改字典树结构连出的边。
- 红色的边：当前结点求出的 fail 指针
- 黄色的边：fail 指针
- 灰色的边：字典树的边
我们可以以此来写出代码
$My\ Code$
#include<bits/stdc++.h>
using namespace std;
namespace IO{
inline void close(){std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);}
inline void Fire(){freopen(".in","r",stdin);freopen(".out","w",stdout);}
inline int read(){int s = 0,w = 1;char ch = getchar();while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}return s*w;}
inline void write(int x){char F[200];int tmp=x>0?x:-x,cnt=0;;if(x<0)putchar('-') ;while(tmp>0){F[cnt++]=tmp%10+'0';tmp/=10;}if(cnt==0)putchar('0');while(cnt>0)putchar(F[--cnt]);putchar(' ');}
}
using namespace IO;
class AC{
public:
class Trie{
public:
int fail,vis[26],end;
}Tr[1000000];
int cnt;
inline void clear(){
memset(Tr,0,sizeof(Tr));
}
inline void ins(string s){
int l=s.length(),q=0;
for(int i=0;i<l;++i){
if(!Tr[q].vis[s[i]-'a']) Tr[q].vis[s[i]-'a']=++cnt;
q=Tr[q].vis[s[i]-'a'];
}
Tr[q].end+=1;
}
inline void Get(){
queue<int>Q;
for(int i=0;i<26;++i){
if(Tr[0].vis[i]!=0){
Tr[Tr[0].vis[i]].fail=0;
Q.push(Tr[0].vis[i]);
}
}
while(!Q.empty()){
int u=Q.front();
Q.pop();
for(int i=0;i<26;++i){
if(Tr[u].vis[i]!=0){
Tr[Tr[u].vis[i]].fail=Tr[Tr[u].fail].vis[i];
Q.push(Tr[u].vis[i]);
}
else
Tr[u].vis[i]=Tr[Tr[u].fail].vis[i];
}
}
}
inline int Ask(string s){
int l=s.length(),q=0,ans=0;
for(int i=0;i<l;++i){
q=Tr[q].vis[s[i]-'a'];
for(int t=q;t&&Tr[t].end!=-1;t=Tr[t].fail){
ans+=Tr[t].end;
Tr[t].end=-1;
}
}
return ans;
}
}AC;
signed main(){
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
string s;
int m=read();
while(m--){
int n=read();
AC.clear();
for(int i=1;i<=n;++i){
cin>>s;
AC.ins(s);
}
AC.Get();cin>>s;
write(AC.Ask(s));
puts("");
}
}
洛谷的完整题面
【模板】AC 自动机（简单版）
题目描述
给定 \(n\) 个模式串 \(s_i\) 和一个文本串 \(t\)，求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。
输入格式
第一行是一个整数，表示模式串的个数 \(n\)。
第 \(2\) 到第 \((n + 1)\) 行，每行一个字符串，第 \((i + 1)\) 行的字符串表示编号为 \(i\) 的模式串 \(s_i\)。
最后一行是一个字符串，表示文本串 \(t\)。
输出格式
输出一行一个整数表示答案。
样例 #1
样例输入 #1
3
a
aa
aa
aaa
样例输出 #1
3
样例 #2
样例输入 #2
4
a
ab
ac
abc
abcd
样例输出 #2
3
样例 #3
样例输入 #3
2
a
aa
aa
样例输出 #3
2
提示
样例 1 解释
\(s_2\) 与 \(s_3\) 编号（下标）不同，因此各自对答案产生了一次贡献。
样例 2 解释
\(s_1\)，\(s_2\)，\(s_4\) 都在串 abcd 里出现过。
数据规模与约定
- 对于 \(50\%\) 的数据，保证 \(n = 1\)。
- 对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 10^6\)，\(1 \leq |t| \leq 10^6\)，\(1 \leq \sum\limits_{i = 1}^n |s_i| \leq 10^6\)。\(s_i, t\) 中仅包含小写字母。
例题
AC自动机板子题，注意每组数据都需要对AC自动机进行\(clear\)操作
点击查看代码
#include<bits/stdc++.h>
using namespace std;
namespace IO{
inline void close(){std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);}
inline void Fire(){freopen(".in","r",stdin);freopen(".out","w",stdout);}
inline int read(){int s = 0,w = 1;char ch = getchar();while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}return s*w;}
inline void write(int x){char F[200];int tmp=x>0?x:-x,cnt=0;;if(x<0)putchar('-') ;while(tmp>0){F[cnt++]=tmp%10+'0';tmp/=10;}if(cnt==0)putchar('0');while(cnt>0)putchar(F[--cnt]);putchar(' ');}
}
using namespace IO;
class AC{
public:
class Trie{
public:
int fail,vis[26],end;
}Tr[1000000];
int cnt;
inline void clear(){
memset(Tr,0,sizeof(Tr));
}
inline void ins(string s){
int l=s.length(),q=0;
for(int i=0;i<l;++i){
if(!Tr[q].vis[s[i]-'a']) Tr[q].vis[s[i]-'a']=++cnt;
q=Tr[q].vis[s[i]-'a'];
}
Tr[q].end+=1;
}
inline void Get(){
queue<int>Q;
for(int i=0;i<26;++i){
if(Tr[0].vis[i]!=0){
Tr[Tr[0].vis[i]].fail=0;
Q.push(Tr[0].vis[i]);
}
}
while(!Q.empty()){
int u=Q.front();
Q.pop();
for(int i=0;i<26;++i){
if(Tr[u].vis[i]!=0){
Tr[Tr[u].vis[i]].fail=Tr[Tr[u].fail].vis[i];
Q.push(Tr[u].vis[i]);
}
else
Tr[u].vis[i]=Tr[Tr[u].fail].vis[i];
}
}
}
inline int Ask(string s){
int l=s.length(),q=0,ans=0;
for(int i=0;i<l;++i){
q=Tr[q].vis[s[i]-'a'];
for(int t=q;t&&Tr[t].end!=-1;t=Tr[t].fail){
ans+=Tr[t].end;
Tr[t].end=-1;
}
}
return ans;
}
}AC;
signed main(){
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
string s;
int m=read();
while(m--){
int n=read();
AC.clear();
for(int i=1;i<=n;++i){
cin>>s;
AC.ins(s);
}
AC.Get();cin>>s;
write(AC.Ask(s));
puts("");
}
}
\(\text{AC}\)自动机上\(\text{DP}\)
用一道例题来讲(其实是因为我只做出来这一道)
多串匹配+计数所以是AC自动机+DP非常显而易见，那么就是在AC自动机上跑DP(废话)
然后我们发现直接求方案数也太难了吧
然后发现其实求不能满足条件的方案数比较简单
从求出含有待匹配串的数量查询进行入手
inline int Ask(string s){
int l=s.length(),q=0,ans=0;
for(int i=0;i<l;++i){
q=Tr[q].vis[s[i]-'a'];
for(int t=q;t&&Tr[t].end!=-1;t=Tr[t].fail){
ans+=Tr[t].end;
Tr[t].end=-1;
}
}
return ans;
}
观察可知查询时是不停的跳\(\text{fail}\)指针当跳到结尾的文本串时累加\(ans\)
那么想要没有字符串满足则需要避开这些\(\text{end}\)
所以思路上就是先用\(ans\)也就是所有方案数的总和去减去所有不合法的方案数
不合法的方案的\(\text{fail}\)所指向的单词也是不合法的
然后状态转移就能强杀出这道题了
$My\ Code$
#include<bits/stdc++.h>
using namespace std;
const int mod=10007;
namespace IO{
inline void close(){std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);}
inline void Fire(){freopen(".in","r",stdin);freopen(".out","w",stdout);}
inline int read(){int s = 0,w = 1;char ch = getchar();while(ch<'0'||ch>'9'){ if(ch == '-') w = -1;ch = getchar();}while(ch>='0'&&ch<='9'){ s = s*10+ch-'0';ch = getchar();}return s*w;}
inline void write(int x){char F[200];int tmp=x>0?x:-x,cnt=0;;if(x<0)putchar('-') ;while(tmp>0){F[cnt++]=tmp%10+'0';tmp/=10;}if(cnt==0)putchar('0');while(cnt>0)putchar(F[--cnt]);putchar(' ');}
}
using namespace IO;
int n,m;
inline int qpow(int a,int b){
int ret=1;a%=mod;
while(b){
if(b%2==1)
(ret*=a)%=mod;
b/=2;(a*=a)%=mod;
}
return ret;
}
class AC{
public:
int f[105][10005];
class Trie{
public:
int fail,vis[26],end;
}Tr[1000000];
int cnt;
inline void clear(){
memset(Tr,0,sizeof(Tr));
}
inline void ins(string s){
int l=s.length(),q=0;
for(int i=0;i<l;++i){
if(!Tr[q].vis[s[i]-'A'])
Tr[q].vis[s[i]-'A']=++cnt;
q=Tr[q].vis[s[i]-'A'];
}
Tr[q].end=1;
}
inline void Get(){
queue<int>Q;
for(int i=0;i<26;++i)
if(Tr[0].vis[i]!=0){
Tr[Tr[0].vis[i]].fail=0;
Q.push(Tr[0].vis[i]);
}
while(!Q.empty()){
int u=Q.front();
Q.pop();
for(int i=0;i<26;++i){
if(Tr[u].vis[i]!=0){
Tr[Tr[u].vis[i]].fail=Tr[Tr[u].fail].vis[i];
Tr[Tr[u].vis[i]].end|=Tr[Tr[Tr[u].vis[i]].fail].end;
Q.push(Tr[u].vis[i]);
}
else
Tr[u].vis[i]=Tr[Tr[u].fail].vis[i];
}
}
}
inline int Ask(){
// int l=s.length(),q=0,ans=0;
// for(int i=0;i<l;++i){
// q=Tr[q].vis[s[i]-'a'];
// for(int t=q;t&&Tr[t].end!=-1;t=Tr[t].fail){
// ans+=Tr[t].end;
// Tr[t].end=-1;
// }
// }
// return ans;
f[0][0]=1;
for(int i=0;i<=m-1;i++)
for(int j=0;j<=cnt;j++)
for(int c=0;c<26;c++)
if(!Tr[Tr[j].vis[c]].end)
f[i+1][Tr[j].vis[c]]=(f[i+1][Tr[j].vis[c]]+f[i][j])%mod;
int ans=qpow(26,m);
for(int i=0;i<=cnt;i++)
ans=(ans-f[m][i]+mod)%mod;
return ans;
}
}AC;
signed main(){
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
string s;
n=read(),m=read();
AC.clear();
for(int i=1;i<=n;++i){
cin>>s;
AC.ins(s);
}
AC.Get();;
write(AC.Ask());
puts("");
}
那么我们可以发现\(AC\)自动机上跑\(dp\)其实只要正常维护AC自动机的插入等操作，而在查询时对于\(f\)的\(i,j,k\)可以直接跑状态转移
转移考虑枚举当前状态的转移即可
\(\text{AC}\)自动机的效率优化
首先分析复杂度，AC自动机的复杂度其实很高，为\(\text O(\sum|s_i|+n|\Sigma|+|S|)\)
根据OI-wiki，我们可以对AC自动机进行优化
首先AC自动机具有一个性质:若在字典图中只保留\(\text{fail}\)边，组成的一定是一棵树
显然，因为 \(\text{fail}\) 不会成环，且深度一定比现在低，所以得证
下面是花絮
