12.8 闲话
K8这几天不在,原来是每天写3000道题,从一个连深搜都写的对的dalao成长为NOIAKer,创造了NOIP一百九十多省选600分的奇迹,这几天不在已经刷了24000道了
我去今天我怎么疯狂被JC,错了哥
推歌
万古生香
假的
这个是真的
这个是真的
这个是真的
今夜若欠清光满堂蘸笔天河绘万古生香
史笔滔滔烟霞绣像
就中拈来玲珑十二章
吹开汗青淋漓苍茫
明辨残稿谁秋水一双
书阁深处篆隶流芳
断简遗篇挥毫续兴亡
谁 白草胡笳烽燧长
将半生哀毁以诗情抵挡
断弦含泪更张
最高贵流浪
隔几世 玉楼试才歌咏琳琅
冠绝了乌衣巷
谁一语风絮荡荡 摹尽落雪茫茫
谁万里关山暂忘女儿模样 家与国都担当
再亲手摘下 黄河落日黑山飞霜 铁甲揩亮
舍旧时云裳
乱世丹心碧血满腔
灵思千转一意辅隋杨
河山纷裂终须入掌
百万明珠抬手赐名将
逸兴遄飞催花一场
犹记看朱成碧添惆怅
凰音一绽惊肃朝纲
无字空碑自不负倔强
谁 一身风雅奉君王
持素心清明秤天下才郎
遇合锦绣黄粱
纷纭中静赏
后来有 一生明旷漱玉噙香
乌江旁歌霸王
结一代清雅无双 举世衣冠齐望
而燕燕于飞怎甘随波低昂 睥睨燕云月上
谁马踏桃花 画角长吟金鼓铿锵 寸土不让
万军一剑挡
煌煌千载辉光
古今盛筵长
何幸有你登场
共举霞觞
谁血作胭脂 枪起夭矫龙翔 翠袖虎符封疆
谁又定两朝风波 掌三世的荣光
今夜我为你轻叙巾帼芬芳 浩歌一曲传香
唱不完跌宕 明媚刚强 百代秾华千秋榜样
行经故梦今又来访
天高海阔盛世飞扬
再谱十万章
原来\(K8\)说的二分图不重要说的是可以用网络流代替
「重要提醒」:学过网络流后你会发现这玩意很不重要,唯一需要了解的就是其定义。
根据我的傻逼理论能被替代知识的尽量直接学替代后的
那我接着摆出我的抽象知识树
二分图定义会了,不学了,学网络流去了(摆)
听说会很劝退我不信,树剖都挺过来了这个能有多抽象?
就算没学明白只要会打个二分图匹配就行
一个网络\(G=(V,E)\)是一张有向图,图中没有有向边\((x,y)\in E\)都有一个给定的权值\(c(x,y)\)叫做边的容量
特别的对于\((x,y)\notin E\) 则 \(c(x,y)=0\)
图中有两个特殊节点\(S\in V\)和\(T\in V\)称作源点和汇点(\(S\neq T\))
设\(f(x,y)\)为定义在节点二元组\((x\in V,y\in V)\)上的实数函数且满足
-
容量限制:\(f(x,y)\le c(x,y)\)
- 对于每条边,流经该边的流量不超过该边的容量
-
斜对称性: \(f(x,y)=-f(y,x)\)
- 每条边的流量与其相反边的流量之和为 \(0\)
-
流守恒性:\(\sum_{(S,u)\in E}f(S,u)=\sum_{(u,T)\in E}f(u,T)\)
- 从源点流出的流量等于汇点流入的流量
则 \(f\) 称作网络 \(G\) 的流函数
对于\((x,y)\in E\),\(f(x,y)\)称作边的流量,\(c(x,y)-f(x,y)\)称作边的剩余容量 \(c_f(x,y)\)
所有流从源点$ S(S∈V) $ 流出,故\(\sum _{(S,v)\in E}f(S,v)\)称作整个网络\(G\)的流量
然后就是最大流问题
最大流
-
OI-wiki :
令 \(G=(V,E)\) 是一个有源汇点的网络,我们希望在 \(G\) 上指定合适的流 \(f\) ,以最大化整个网络的流量 \(|f|\) (即 \(\sum_{x \in V} f(s, x) - \sum_{x \in V} f(x, s)\) )。
-
人话
给定一个网络\(G\),求一个流函数\(f\)使这个网络的总流量最大。
-
Ford–Fulkerson增广听说这个能算二分图最大匹配

「增广路(Augmenting Path)」:一条起点为源点,终点为汇点的剩余流量不为空的边的路径
-
概述
我们将 \(G\) 中所有结点和剩余容量大于 \(0\) 的边构成的子图称为残量网络 \(G_f\) ,即 \(G_f=(V,E_f)\) ,其中 \(E_f=\left\{(u,v) \mid c_f(u,v)>0\right\}\)。
流量可能是负值,因此, \(E_f\) 的边有可能并不在 \(E\) 中。
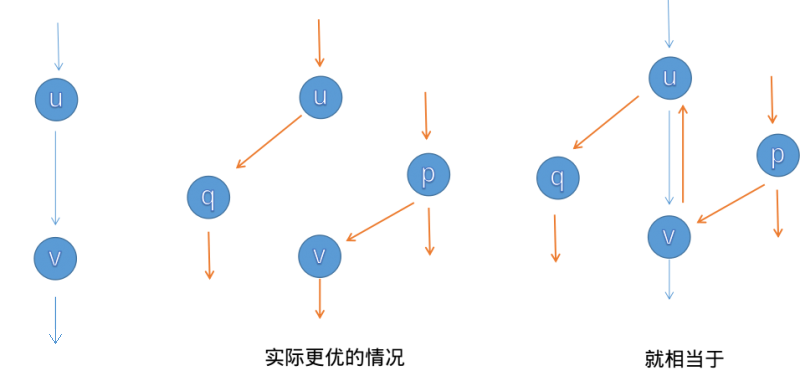
将 \(G_f\) 上一条从源点 \(s\) 到汇点 \(t\) 的路径称为增广路(Augmenting Path)。
对于一条增广路,我们给每一条边 \((u, v)\) 都加上等量的流量,以令整个网络的流量增加,这一过程被称为增广
故最大流求解可以被视为多次增广得到的流的叠加
此外,在增广过程中,对于边 \((u, v)\) ,都新建一条反向边 \((v, u)\)
\(f(u, v) = -f(v, u)\)这一性质可以通过在增广时退流来保证,即 \(f(u, v)\) 增加时 \(f(v, u)\) 减少同等的量
-

