Python求阴影部分面积
一、前言说明
今天看到微信群里一道六年级数学题,如下图,求阴影部分面积
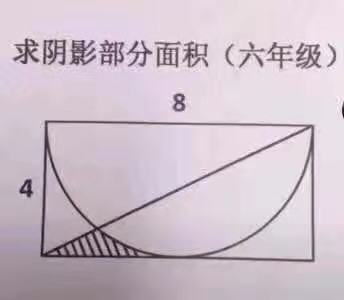
看起来似乎并不是很难,可是博主添加各种辅助线,写各种方法都没出来,不得已而改用写Python代码来求面积了
二、思路介绍
1.用Python将上图画在坐标轴上,主要是斜线函数和半圆函数
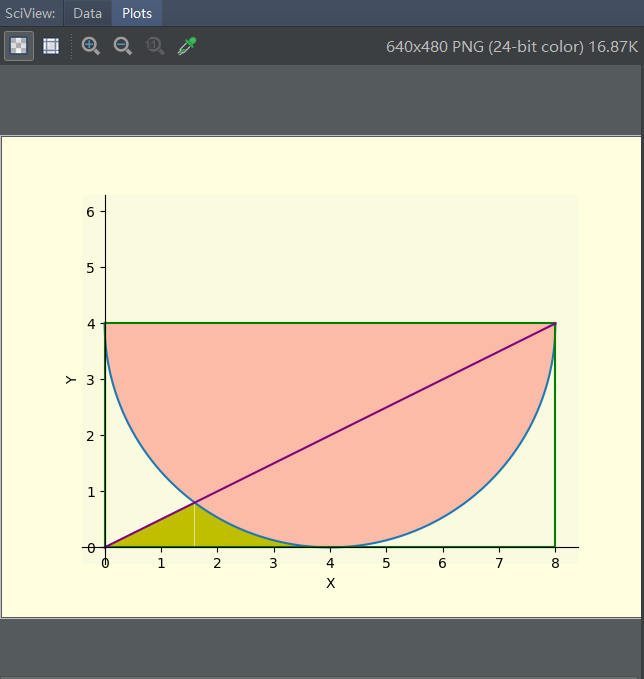
2.均匀的在长方形上面洒满豆子(假设是豆子),求阴影部分豆子占比*总面积
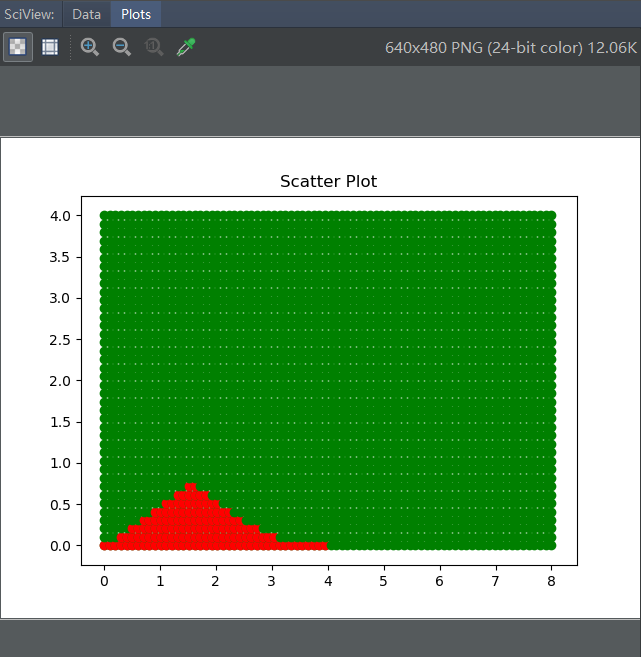
三、源码设计
1.做图源码

1 import matplotlib.pyplot as plt 2 import numpy as np 3 4 5 def init(): 6 plt.xlabel('X') 7 plt.ylabel('Y') 8 9 fig = plt.gcf() 10 fig.set_facecolor('lightyellow') 11 fig.set_edgecolor("black") 12 13 ax = plt.gca() 14 ax.patch.set_facecolor("lightgray") # 设置ax区域背景颜色 15 ax.patch.set_alpha(0.1) # 设置ax区域背景颜色透明度 16 ax.spines['right'].set_color('none') 17 ax.spines['top'].set_color('none') 18 ax.xaxis.set_ticks_position('bottom') 19 ax.yaxis.set_ticks_position('left') 20 ax.spines['bottom'].set_position(('data', 0)) 21 ax.spines['left'].set_position(('data', 0)) 22 23 24 # 原下半函数 25 def f1(px, r, a, b): 26 return b - np.sqrt(r**2 - (px - a)**2) 27 28 29 # 斜线函数 30 def f2(px, m, n): 31 return px*n/m 32 33 34 # 斜线函数2 35 def f3(px, m, n): 36 return n-1*px*n/m 37 38 39 if __name__ == '__main__': 40 r = 4 # 圆半径 41 m = 8 # 宽 42 n = 4 # 高 43 a, b = (4, 4) # 圆心坐标 44 init() 45 46 x = np.linspace(0, m, 100*m) 47 y = np.linspace(0, n, 100*n) 48 49 # 半圆形 50 y1 = f1(x, r, a, b) 51 plt.plot(x, y1) 52 # 矩形横线 53 plt.plot((x.min(), x.max()), (y.min(), y.min()), 'g') 54 plt.plot((x.min(), x.max()), (y.max(), y.max()), 'g') 55 plt.plot((x.max(), x.max()), (y.max()+2, y.max()+2), 'g') # 画点(8,6)避免图形变形 56 # 矩形纵向 57 plt.plot((x.min(), x.min()), (y.min(), y.max()), 'g') 58 plt.plot((x.max(), x.max()), (y.min(), y.max()), 'g') 59 # 斜线方法 60 y2 = f2(x, m, n) 61 plt.plot(x, y2, 'purple') 62 63 # 阴影部分填充 64 xf = x[np.where(x <= 0.5*x.max())] 65 plt.fill_between(xf, y.min(), f1(xf, r, a, b), where=f1(xf, r, a, b) <= f2(xf, m, n), 66 facecolor='y', interpolate=True) 67 plt.fill_between(xf, y.min(), f2(xf, m, n), where=f1(xf, r, a, b) > f2(xf, m, n), 68 facecolor='y', interpolate=True) 69 # 半圆填充 70 plt.fill_between(x, y1, y.max(), facecolor='r', alpha=0.25) 71 plt.show()
2.计算源码,其中side是要不要计算图形边框上的点,理论上side只能为True;t设置越大运行时间越长也越精准

1 import numpy as np 2 3 4 def f1(px, r, a, b): 5 return b - np.sqrt(r**2 - (px - a)**2) 6 7 8 def f2(px, m, n): 9 return px*n/m 10 11 12 if __name__ == '__main__': 13 r = 4 # 圆半径 14 m = 8 # 宽 15 n = 4 # 高 16 a, b = (4, 4) # 圆心坐标 17 t = 100 # 精度 18 19 xs = np.linspace(0, m, 2*t*m) 20 ys = np.linspace(0, n, t*n) 21 22 # 半圆形 23 y1 = f1(xs, r, a, b) 24 # 斜线 25 y2 = f2(xs, m, n) 26 27 numin = 0 28 numtotel = 0 29 side = True # 是否计算边框 30 for x in xs: 31 for y in ys: 32 if not side: 33 if (x <= 0) | (x >= 8) | (y <= 0) | (y >= 4): 34 continue 35 numtotel += 1 36 if x >= 4: 37 continue 38 y1 = f1(x, r, a, b) 39 y2 = f2(x, m, n) 40 if y1 - y2 >= 0: 41 if y2 - y > 0: 42 numin += 1 43 if (y2 - y == 0) and side: 44 numin += 1 45 elif y2 - y1 > 0: 46 if y1 - y > 0: 47 numin += 1 48 if (y2 - y == 0) and side: 49 numin += 1 50 51 print(32*numin/numtotel)
四、最后小结
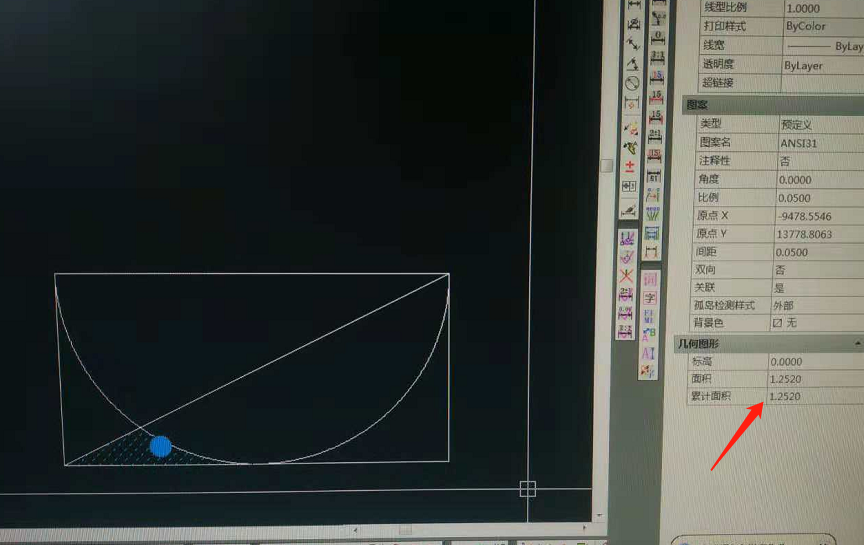
1.此种算法t为100时,阴影面积为1.268;t为1000时,阴影面积为1.253,已经非常接近正确答案(正确答案1.252)
2.举一反三,类似于这种不规则的面积,只要可以写出来函数,就可以求解面积.
2.下面有三种求解方法,第三种表示比大学高数还难看懂,你们呢?
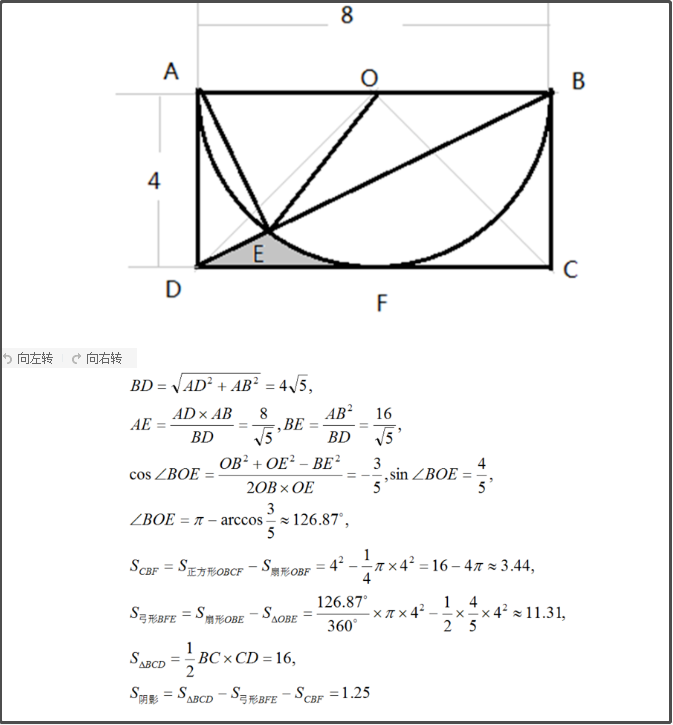
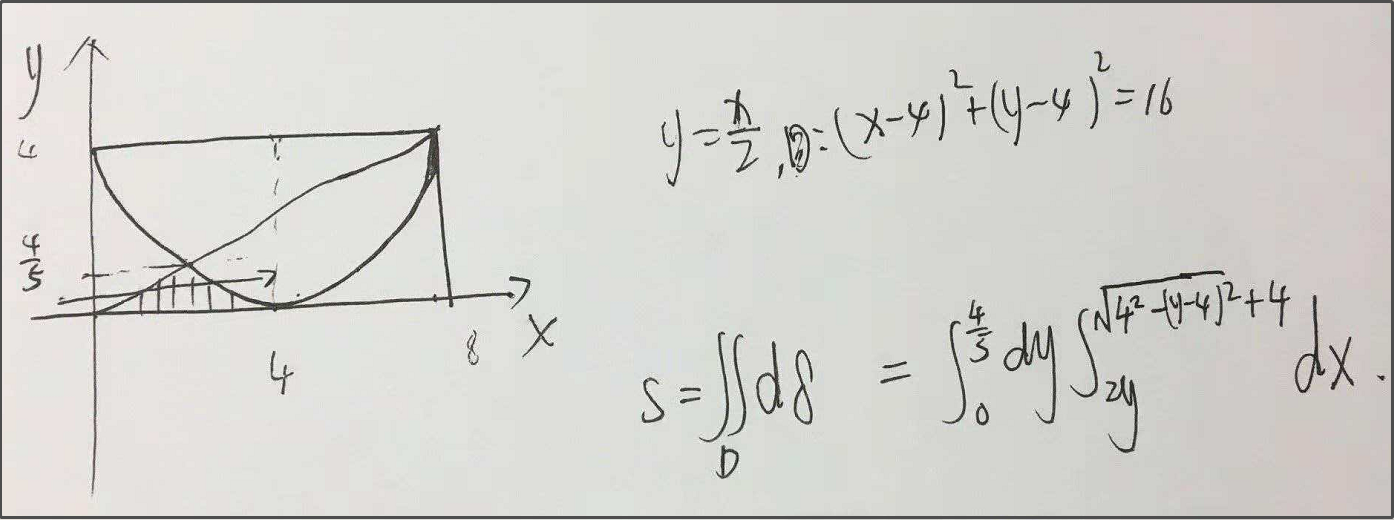
作者名称:Vrapile
联系方式:发送邮件Vrapile@163.com,另博客账号也是本人微信号。
版权声明:此文是博主业余爱好所写,文章或有错误与不足之处,欢迎留言指正建议、共同探讨!另此文为博主原创,未经博主同意不得转载,否则保留追究法律责任的权利。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号