AC自动机学习笔记
定义
Aho-Corasick automaton,该算法在1975年产生于贝尔实验室,是著名的多模匹配算法。
具体问题大致为多个模式串在一个文本串中匹配查询的问题。
AC自动机利用某些操作阻止了模式串匹配阶段的回溯,将时间复杂度优化到了 \(O(n)\)(n为文本串长度)
前置芝士
基本的 \(Trie\) 树,\(KMP\) 的失配指针思想。
不会 \(KMP\) 可以先去学习 \(KMP\)算法
AC 自动机
思想其实挺简单的,就是在一棵由模式串构造出的字典树上进行文本串的匹配。
但是如果每次匹配都从根开始匹配,算法复杂度问题比较大,所以就有了 AC 自动机。
其思想与 \(KMP\) 一致,对于字典树上的节点建立失配指针,匹配失败的话直接跳转到失配指针继续匹配。
下边给出一个例子:
我们现在有模式串: abc,bcd,acd,cd。
那么我们可以建出一个这样的字典树
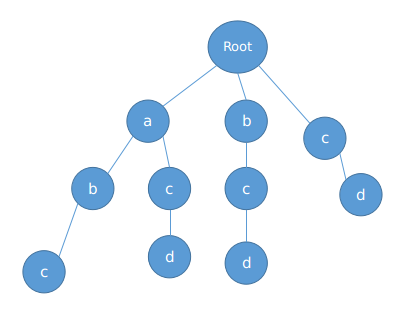
然后给出一个很长的文本串,一个一个从根开始扫复杂度非常不友好,所以我们就会用到 \(fail\) 指针。
\(fail\) 指针的建立是找到两个串的最长公共后缀,然后连起来,所以我们这个树的 \(fail\) 指针应该就是这样的:

每一次匹配失败之后,从最长的公共后缀开始匹配,这样一定是对的。
接下来我们关心的就是如何去找 \(fail\) 指针。
首先我们建一棵字典树,然后利用 \(BFS\) 找,首先把根节点下的点入对,然后找每次出队的点作为父亲,枚举所有可能的儿子(字母一共26个),如果有这个儿子,那么这个儿子的 \(fail\) 指针就是父亲 \(fail\) 指针的当前儿子。如果没有当前儿子,那么就把当前节点的当前儿子设为当前节点 \(fail\) 指针的当前儿子。(可能说的不太清楚,当前儿子指的是枚举的儿子是谁)。
下边给出构造 \(fail\) 指针的代码:
queue<int>q;
inline void build(){
for(int i = 0;i < 26;++i){
if(t[0][i]) q.push(t[0][i]);
}
while(!q.empty()){
int x = q.front();
q.pop();
for(int i = 0;i < 26;++i){
if(t[x][i]){
fail[t[x][i]] = t[fail[x]][i];
q.push(t[x][i]);
}
else t[x][i] = t[fail[x]][i];
}
}
}
然后在查询的时候,对于文本串的每个字符,就从根节点一直跳 \(fail\) 指针查找,一直向下寻找,直到匹配失败( \(fail\) 指针指向根或者当前节点已找过).
查询代码
inline void query(char *ch){
int len = strlen(ch + 1);
int rt = 0;
for(int i = 1;i <= len;++i){
int x = ch[i] - 'a';
rt = t[rt][x];//从该字母节点开始跳
for(int j = rt;j;j = fail[j])ans[end[j]]++;//直到匹配失败。
}
}
到这里,AC自动机的内容就讲解完了,主要就是 \(fail\) 指针的建立和查询时跳 \(fail\) 指针的操作。
例题
下边给出洛谷上的三道模板题以供练习:
【模板】AC自动机(简单版)
题目
分析
板子(题目说了),查询文本串中有多少个不同的模式串。
我们在建立字典树的时候,对于最末尾节点用数组 \(end\) 记录一下有多少个串以这个点作为结尾,在查询跳 \(fail\) 的时候,累加上跳到的点的 \(end\) 即可。
代码
#include<bits/stdc++.h>
using namespace std;
#define gc() getchar()
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
const int maxn = 1e6+10;
char s[maxn];
int n;
int t[maxn][30];
int tot,end[maxn],fail[maxn];
inline void insert(char *ch){//建立字典树
int rt = 0;
int len = strlen(ch+1);
for(int i = 1;i <= len;++i){
int x = ch[i] - 'a';
if(!t[rt][x])t[rt][x] = ++tot;
rt = t[rt][x];
}
end[rt]++;//记录当前点是几个单词的结尾
}
inline void build(){//找fail指针
queue<int>q;
memset(fail,0,sizeof(fail));
for(int i = 0;i < 26;++i){
if(t[0][i])q.push(t[0][i]);
}
while(!q.empty()){
int x = q.front();
q.pop();
for(int i = 0;i < 26;++i){
if(t[x][i]){
fail[t[x][i]] = t[fail[x]][i];
q.push(t[x][i]);
}
else{
t[x][i] = t[fail[x]][i];
}
}
}
}
inline int query(char *ch){//查询
int len = strlen(ch+1);
int rt = 0,ans = 0;
for(int i = 1;i <= len;++i){
int x = ch[i] - 'a';
rt = t[rt][x];
for(int j = rt;j && end[j] != -1;j = fail[j]){
ans += end[j];//累加
end[j] = -1;//清空
}
}
return ans;
}
int main(){
n = read();
for(int i = 1;i <= n;++i){
scanf("%s",s+1);
insert(s);
}
build();
scanf("%s",s+1);
printf("%d\n",query(s));
return 0;
}
【模板】AC自动机(加强版)
题目
分析
题目要我们找到出现最多的模式串出现的次数和是谁,那么我们就在建立字典树的时候,记录一下以每个点作为结尾的串是哪个串。
在进行查询的时候,每次跳 \(fail\) 指针跳到某个点的时候,就给当前点记录的串的下标的答案++(有些绕,一会可以结合代码看看)。
最后对于 \(ans\) 数组扫两遍即可。
代码
#include<bits/stdc++.h>
using namespace std;
#define gc() getchar()
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
const int maxn = 5e5+10;
int t[maxn][30];
char s[maxn];
char ss[200][maxn];
int tot;
int fail[maxn],end[maxn],ans[maxn];
inline void insert(char *ch,int now){
int len = strlen(ch+1);
int rt = 0;
for(int i = 1;i <= len;++i){
int x = ch[i] - 'a';
if(!t[rt][x])t[rt][x] = ++tot;
rt = t[rt][x];
}
end[rt] = now;//记录当前点是谁的结尾
}
queue<int>q;
inline void build(){//日常建fail指针
for(int i = 0;i < 26;++i){
if(t[0][i])q.push(t[0][i]);
}
while(!q.empty()){
int x = q.front();q.pop();
for(int i = 0;i < 26;++i){
if(t[x][i]){
fail[t[x][i]] = t[fail[x]][i];
q.push(t[x][i]);
}
else{
t[x][i] = t[fail[x]][i];
}
}
}
}
inline void query(char *ch){
int len = strlen(ch + 1);
int rt = 0;
for(int i = 1;i <= len;++i){
int x = ch[i] - 'a';
rt = t[rt][x];
for(int j = rt;j;j = fail[j])ans[end[j]]++;//当前节点代表的单词出现个数++
}
}
int main(){
int n;
while(1){
scanf("%d",&n);if(n == 0)break;
memset(t,0,sizeof(t));//多测注意清空
memset(end,0,sizeof(end));
memset(fail,0,sizeof(fail));
memset(ans,0,sizeof(ans));
for(int i = 1;i <= n;++i){
scanf("%s",ss[i]+1);
insert(ss[i],i);
}
build();
scanf("%s",s+1);
query(s);
int mx = 0;//下边扫两边即可
for(int i = 1;i <= n;++i)if(ans[i] > mx)mx = ans[i];
printf("%d\n",mx);
for(int i = 1;i <= n;++i)if(ans[i] == mx)printf("%s\n",ss[i]+1);
}
return 0;
}
【模板】AC自动机(二次加强版)
题目
分析
与加强版差不了多少,只不过是查询的东西不一样了。
我们现在要统计每个串出现多少次,那么我们就记录一下每个串的终点是谁。
在查询的时候,我们不需要跳 \(fail\) ,改成对于每个点访问次数++,然后再从每个点的 \(fail\) 向当前点建边。
利用差分,我们把每个点访问次数++,就相当与把根到当前点上所有点次数都++,这样只需要建立一棵 \(fail\) 指针连接的树,然后 \(dfs\) 一遍求出差分答案即可。
代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, w = 1;
char ch = getchar();
for(; ch > '9' || ch < '0'; ch = getchar()) if(ch == '-') w = -1;
for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
return x * w;
}
const int maxn = 2e6+10;
char s[maxn];
int tot;
int fail[maxn],end[maxn],sum[maxn],t[maxn][30];
inline void insert(char *ch,int now){
int len = strlen(ch+1);
int rt = 0;
for(int i = 1;i <= len;++i){
int x = ch[i] - 'a';
if(!t[rt][x])t[rt][x] = ++tot;
rt = t[rt][x];
}
end[now] = rt;//记录当前串结尾是哪个点
}
queue<int>q;
inline void build(){
for(int i = 0;i < 26;++i){
if(t[0][i]) q.push(t[0][i]);
}
while(!q.empty()){
int x = q.front();
q.pop();
for(int i = 0;i < 26;++i){
if(t[x][i]){
fail[t[x][i]] = t[fail[x]][i];
q.push(t[x][i]);
}
else t[x][i] = t[fail[x]][i];
}
}
}
inline void query(char *ch){
int len = strlen(ch+1);
int rt = 0;
for(int i = 1;i <= len;++i){
int x = ch[i] - 'a';
rt = t[rt][x];
sum[rt]++;//每个点访问次数++
}
}
struct Node{
int v,next;
}e[maxn<<1];
bool vis[maxn];
int head[maxn],cnt;
inline void Add(int x,int y){
e[++cnt].v = y;
e[cnt].next = head[x];
head[x] = cnt;
}
inline void dfs(int x){
vis[x] = 1;
for(int i = head[x];i;i = e[i].next){
int v = e[i].v;
if(vis[v])continue;
dfs(v);
sum[x] += sum[v];
}
}
int main(){
int n = read();
for(int i = 1;i <= n;++i){
scanf("%s",s+1);
insert(s,i);
}
build();
scanf("%s",s+1);
query(s);
for(int i = 0;i <= tot;++i)Add(fail[i],i);//建树
dfs(0);//差分
for(int i = 1;i <= n;++i){
printf("%d\n",sum[end[i]]);//按结尾点出现次数知道串出现次数
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号