全球覆盖（哈希+思维）

题目描述

小黑正在研发一款全球定位软件，想用它来定位小白的坐标。具体来说，地球可以看做一个 \(X \times Y\) 的网格矩阵，横纵坐标范围分别是 \([0,X)\) 和 $ [0,Y)$ ，由于地球是球形结构，网格的上边界和下边界是相通的，左边界和右边界也是相通的。

现在小黑获得了 \(n\) 组坐标对，每组坐标对含有两个点的坐标 \((x_{i,0},y_{i,0})\) \((x_{i,1},y_{i,1})\) ，表示地球上一个两边平行于坐标轴的矩形的两个对角顶点，而小白就在这个矩形内部。

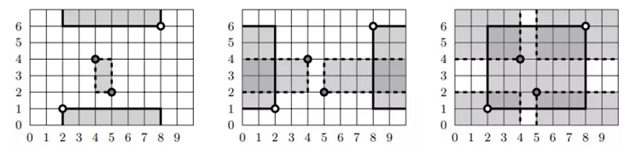
然而，由于地球是球形结构，确定了坐标对后仍然有多种可能的“矩形”（如下图所示）。小黑想知道最多可能有多少面积的网格出现在所有“矩形”的交集之中，以方便他确定小白的位置。每个单元格的面积为 \(1\) 。

于是他把这个问题交给你了。

输入格式

第一行三个正整数 \(n,X,Y\) ，含义如题目描述。

接下来 \(n\) 行，每行四个正整数 \(x_{i,0},y_{i,0},x_{i,1},y_{i,1}\)，描述一组坐标对。所有数据始终保证有 \(x_{i,0} < x_{i,1},y_{i,0}<y_{i,1}\) 。

输出格式

一行，一个整数，表示所求的答案。

样例

样例输入

2 10 7
2 1 8 6
4 2 5 4

样例输出

15

样例 1 解释

样例中的情况和题目中图片一致，其中第三种情况的面积最大。

数据范围与提示

对于 \(100\%\) 的数据 \(n \leqslant 500000,2 \leqslant X,Y \leqslant 10^9,0\leqslant x_0,x_1<X,0\leqslant y_0,y_1<Y\)。

分析

每个矩形可能有几种划分情况，每个确定好的两个矩形端点可以据此划分成一个类似于九宫格的东西，其中有一些就可以组成同一个矩形（因为网格图相当与地球，可以转过来），那么我们就可以直接考虑按这些划分完以后的线段进行计算，显然只需要计算横向和纵向的最长线段然后乘起来就好。

但是线段可能是分开的，不是连续的一整个线段，那么我们就可以根据某个线段是否在某个矩形内部来进行讨论。如果在第 \(i\) 个矩形内部，我们就可以把一个数字串的第 \(i\) 位变成 \(1\) ，否则为 \(0\) ，然后根据这个我们可以求每一段线段的哈希值，相同的就加载一起，那么就可以求出最大值了。

哈希值的求出我们可以根据访问到了哪个矩形进行加和，访问到这个矩形的某个边界第一次，那么当前边的哈希值就加上属于这个矩形的那个 \(1\) 所代表的哈希值，第二次访问就减去。需要注意的是，如果有两个以上的边界在同一个坐标，需要直接判掉，不然会做多余的贡献。

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int L = 1 << 20;
char buffer[L],*S,*T;
#define getchar() (S == T && (T = (S = buffer) + fread(buffer,1,L,stdin),S == T) ? EOF : *S++)
#define ll unsigned long long
#define int long long
inline int read(){
	int s = 0,f = 1;
	char ch = getchar();
	while(!isdigit(ch)){
		if(ch == '-')f = -1;
		ch = getchar();
	}
	while(isdigit(ch)){
		s = s * 10 + ch - '0';
		ch = getchar();
	}
	return s * f;
}//以上为快读
const int maxn = 1e7+10;
const ll mod = 1e7+141;
ll base = 2;
long long mp1[20000100];//记录横向每个哈希值的线段长度和
long long mp2[20000100];//纵向每个哈希值的线段长度和
struct N{
	int x,y,id;
}jl[maxn << 2];//记录每个矩形的端点坐标，方便对哈希值进行加减
int p[maxn];
int vis[maxn];//记录当前坐标被访问几次
bool cmp1(N a,N b){
	return a.x < b.x;
}
bool cmp2(N a,N b){
	return a.y < b.y;
}
signed main(){
	freopen("globe.in","r",stdin);
	freopen("globe.out","w",stdout);
	int n = read(),X = read(),Y = read();
	p[0] = 1;
	for(int i = 1;i <= n;++i){//处理每一位应该加上什么哈希值
		p[i] = p[i-1] % mod * base % mod;
	}
	p[0] = 0;
	for(int i = 1;i <= n;++i){//记录矩形边界
		jl[i].x = read();
		jl[i].y = read();
		jl[i+n].x = read();
		jl[i+n].y = read();
		jl[i].id = jl[i+n].id = i;
	}
	jl[n*2+1].x = X;
	jl[n*2+1].y = Y;
	sort(jl+1,jl+n*2+1,cmp1);//按横坐标排个序
	ll hsh = 0;
	long long mx1 = 0,mx2 = 0;
	if(jl[1].x != 0){//第一个要特殊处理
		mp1[0] += jl[1].x;
	}
	for(int i = 1;i <= 2 * n;++i){//找横坐标最大
		if(jl[i].x == jl[i+1].x)continue;//如果相等就直接不计算
		if(!vis[jl[i].id])hsh += p[jl[i].id],vis[jl[i].id] = 1,hsh %= mod;
		else{
			hsh -= p[jl[i].id];
			hsh %= mod;
		}
		mp1[hsh] += jl[i + 1].x - jl[i].x;
		mx1 = max(mx1,mp1[hsh]);
	}
	memset(vis,0,sizeof(vis));
	hsh = 0;
	sort(jl+1,jl+n*2+1,cmp2);//同上，此时处理纵坐标
	if(jl[1].y != 0){
		mp2[0] += jl[1].y;
	}
	for(int i = 1;i <= 2*n;++i){
		if(jl[i].y == jl[i+1].y)continue;
		if(!vis[jl[i].id])hsh += p[jl[i].id],vis[jl[i].id] = 1,hsh %= mod;
		else{
			hsh -= p[jl[i].id];
			hsh %= mod;
		}
		mp2[hsh] += jl[i+1].y - jl[i].y;
		mx2 = max(mx2,mp2[hsh]);
	}
	printf("%lld\n",mx1 * 1LL * mx2);
}