集训模拟赛8 [虎哥出题的一天]
前言
相信不用我说什么了,虎哥出题我必糊……下边是分析
NO.1 食物链
题目
如图所示为某生态系统的食物网示意图
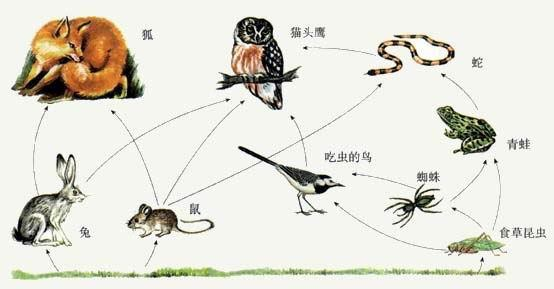
现在给你n个物种和m条能量流动关系,求其中的食物链条数。
物种的名称为从1到n编号,m条能量流动关系形如
\(a_1\ b_1\)
\(a_2\ b_2\)
\(a_3\ b_3\)
\(……\)
\(a_{m−1}\ b_{m−1}\)
\(a_m\ b_m\)
其中ai bi表示能量从物种ai流向物种bi。
输入格式
第一行两个正整数\(n\)和\(m\)。
接下来\(m\)行每行两个整数\(a_i,b_i\)表示\(m\)条能量流动关系。
(数据保证输入数据符号合生物学特点,且不会有重复的能量流动关系出现)
输出格式
一个整数即食物网中的食物链条数。
样例输入
10 16
1 2
1 4
1 10
2 3
2 5
4 3
4 5
4 8
6 8
7 6
7 9
8 5
9 8
10 6
10 7
10 9
样例输出
9
数据范围
\(1\le n\le 100000,0\le m\le 200000\)。
分析
这个题其实只是一道裸的记忆化暴搜,其实除了建边我全都写对了,然而我当时一时nt,直接反向建边(因为我觉的这样好做……)然后就\(WA\)了,以后可不能玩这有的没的了……
我们统计每个点的入度和出度,显然入度为\(0\)的点是食物链的起点,我们就从这个点开始递归,统计到有入度没出度的点就直接让\(ans++\),因为他没有子节点,只有自己本身,然后要记得每一次的答案都要用一个数组记录下来,不然应该会\(TLE\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5+10;
struct Node{//建边结构体
int v,next;
}e[maxn];
int vis[maxn];
int head[maxn],ans;
int n,m;
int tot,du[maxn],rd[maxn],cd[maxn];
void Add(int x,int y){//建边
e[++tot].v = y;
e[tot].next = head[x];
head[x] = tot;
}
int Dfs(int x){//i递归
if(du[x])return du[x];//当前点被搜过就直接返回值
int ans = 0;
if(!cd[x] && rd[x])ans++;//扫到了食物链终点直接答案加一
for(int i=head[x];i;i=e[i].next)ans+=Dfs(e[i].v);//字节点的值加起来
return du[x] = ans;//记忆化并返回当前点的值
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){
int x,y;
scanf("%d%d",&x,&y);
Add(x,y);//建边并统计出入度
cd[x]++;
rd[y]++;
}
for(int i=1;i<=n;++i){
if(rd[i]==0){//入度为0,从起点出发
ans+=Dfs(i);
}
}
printf("%d\n",ans);
}
NO.2 升降梯上
题目描述
开启了升降梯的动力之后,探险队员们进入了升降梯运行的那条竖直的隧道,映入眼帘的是一条直通塔顶的轨道、一辆停在轨道底部的电梯、和电梯内一杆控制电梯升降的巨大手柄。
\(Nescafe\)之塔一共有\(N\)层,升降梯在每层都有一个停靠点。手柄有\(M\)个控制槽,第\(i\)个控制槽旁边标着一个数\(C_i\),满足\(C_1<C_2<C_3<……<C_M\)。如果\(C_i>0\),表示手柄扳动到该槽时,电梯将上升\(C_i\)层;如果\(C_i<0\),表示手柄扳动到该槽时,电梯将下降\(-C_i\)层;并且一定存在一个\(C_i=0\),手柄最初就位于此槽中。注意升降梯只能在\(1\to N\)层间移动,因此扳动到使升降梯移动到\(1\)层以下、\(N\)层以上的控制槽是不允许的。
电梯每移动一层,需要花费\(2\)秒钟时间,而手柄从一个控制槽扳到相邻的槽,需要花费\(1\)秒钟时间。探险队员现在在\(1\)层,并且想尽快到达\(N\)层,他们想知道从\(1\)层到\(N\)层至少需要多长时间?
输入格式
第一行两个正整数\(N\)、\(M\)。
第二行\(M\)个整数\(C_1、C_2……C_M\)。
输出格式
输出一个整数表示答案,即至少需要多长时间。若不可能到达输出\(-1\)。
样例
样例输入
6 3
-1 0 2
样例输出
19
数据范围与提示
手柄从第二个槽扳到第三个槽(\(0\)扳到\(2\)),用时\(1\)秒,电梯上升到\(3\)层,用时\(4\)秒。
手柄在第三个槽不动,电梯再上升到\(5\)层,用时\(4\)秒。
手柄扳动到第一个槽(\(2\)扳到\(-1\)),用时\(2\)秒,电梯下降到\(4\)层,用时\(2\)秒。
手柄扳动到第三个槽(\(-1\)扳倒\(2\)),用时\(2\)秒,电梯上升到\(6\)层,用时\(4\)秒。
总用时为\((1+4)+4+(2+2)+(2+4)=19\)秒。
对于\(30\%\) 的数据,满足\(1\le N\le 10\),\(2\le M\le 5\)。
对于 \(100\%\) 的数据,满足\(1\le N\le 1000,2\le M\le 20\),\(-N<C_1<C_2<……<C_M<N\)。
分析
又是一个玄学建边求最短路的题,只是没看出来……以后要多练练这方面的思维了。主要思路就是从手柄每个位置之间建边,边权就是时间也就是标号差的绝对值。然后每一个手柄的位置在不同的层之间也要建边,边权就是楼层差乘以2,楼层差是根据这个手柄能走多少来决定的,具体代码注释里说。
然后建完边跑最短路,与最短路的题不一样的是,这次要统计最顶层到达所有手柄位置中最小的路径,因为最后手柄不一定拉到哪里,当然是最小的更优。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 4e5+10;
int head[maxn],dis[25005],vis[25005];
struct Node{
int v,next,val;
}e[maxn<<1];
int tot;
int a[maxn],ll,jl[1005][50];
void Add(int x,int y,int z){//建边
e[++tot].v = y;
e[tot].next = head[x];
head[x] = tot;
e[tot].val = z;
}
priority_queue<pair<int,int> >q;
void Dij(int x){//堆优化迪杰斯特拉求最短路
memset(dis,0x3f,sizeof(dis));
dis[x] = 0;
q.push(make_pair(0,x));
while(!q.empty()){
int y = q.top().second;
q.pop();
if(vis[y])continue;
vis[y] = 1;
for(int i=head[y];i;i=e[i].next){
int v = e[i].v;
int w = e[i].val;
if(dis[v]>dis[y]+w){
dis[v] = dis[y]+w;
q.push(make_pair(-dis[v],v));
}
}
}
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;++i){
cin>>a[i];
}
int cnt = 0;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
jl[i][j] = ++cnt;//把所有的点都赋予一个标号
if(i == 1 && a[j] == 0)ll = cnt;//记录手柄初始位置
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
for(int k=1;k<=m;++k){//手柄位置不同就建边
if(j!=k)
Add(jl[i][j],jl[i][k],abs(k-j));//手柄之间建边,边权是差值绝对值
}
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(a[j]!=0 && i+a[j]>=1 && i+a[j]<=n){//不是初始位置且拉完拉杆以后没有跑到外边
Add(jl[i][j],jl[i+a[j]][j],abs(a[j]*2));//边权为走的楼层数乘以2,按钮位置不变,只改第一维的高度
}
}
}
Dij(ll);//从手柄初始位置开始最短路
int ans = 0x3f3f3f3f;
for(int i=1;i<=m;++i){
ans = min(ans,dis[jl[n][i]]);//找到顶层最短的路径
}
if(ans == 0x3f3f3f3f){//没有路径就输出-1
cout<<-1<<endl;
return 0;
}
cout<<ans<<endl;
return 0;
}
分析解法2
还有一种就是\(dp\)解法,这是\(lc\)大佬讲的,利用\(f[i][j]\)记录到第\(i\)层,手柄位置为\(j\)的时间,然后从手柄位置为\(k\)转移而来,取\(min\)即可,下边代码
代码
自己写的时候有点压行,所以凑合着看吧
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e3+4,maxk = 25;
#define ll long long
ll f[maxn][maxk],ans = 0x3f3f3f3f3f3f3f3f,jl[maxn],n,m;
int main(){
memset(f,0x3f,sizeof(f));
cin>>n>>m;
for(int i=1;i<=m;++i){
cin>>jl[i];
if(jl[i] == 0)f[1][i] = 0;//第一层初始位置时间为0
}
for(int js=1;js<=5;++js)//贪心多贪几遍,保证正确(lc大佬说的)
for(int i=1;i<=n;++i)//枚举楼层
for(int j=1;j<=m;++j)//当前手柄位置
for(int k=1;k<=m;++k){//上一次手柄位置
int now = i-jl[k];//这次拉手柄前的位置
if(now>=1 && now<=n)f[i][j] = min(f[i][j],f[now][k]+abs(j-k)+abs(jl[k]*2));//更新答案
}
for(int i=1;i<=m;++i)ans = min(ans,f[n][i]);//顶层取最大值
printf("%lld",ans == 0x3f3f3f3f3f3f3f3f?-1:ans);return 0;//玄学三维运算符自行理解
}
NO.3 Password
题目描述
\(Rivest\)是密码学专家。近日他正在研究一种数列\(E=\{E[1],E[2],……,E[n]\}\),且\(E[1]=E[2]=p\)(\(p\)为一个质数),\(E[i]=E[i-2]\times E[i-1]\)(若\(2<i\le n\))。例如\(\{2,2,4,8,32,256,8192,……\}\)就是\(p=2\)的数列。在此基础上他又设计了一种加密算法,该算法可以通过一个密钥\(q(q<p)\)将一个正整数\(n\)加密成另外一个正整数\(d\),计算公式为:\(d=E[n]\ mod\ q\)。现在\(Rivest\)想对一组数据进行加密,但他对程序设计不太感兴趣,请你帮助他设计一个数据加密程序。
输入描述
读入\(m\),\(p\)。其中\(m\)表示数据个数,\(p\)用来生成数列\(E\)。以下有\(m\)行,每行有\(2\)个整数\(n\),\(q\)。\(n\)为待加密数据,\(q\)为密钥。
输出描述
第\(i\)行输出第\(i\)个加密后的数据。
样例输入
2 7
4 5
4 6
样例输出
3
1
分析
这个题其实就是比较裸的数论,只不过是考到的东西非常多,所以我们逐一分析,首先数列\(E\)的求出,我们分析一下给的例子,很容易就能得出这是\(p\)的乘方,乘方数就是菲波纳契数列,然后因为\(p\)为质数,所以我们可以根据扩展欧拉定理得出公式:
因为我们要求的是\(p\)的菲波纳契数列第\(n\)项次方\(modq\),所以我们需要的只是菲波纳契数列第\(n\)项,根据上边的公式,我们可以把菲波纳契数列第\(n\)项次方转化为\(p^{\varphi(q)\times k + t}\),利用矩阵快速幂求出这个\(t\)只需要在乘的过程中一直取\(\varphi(q)\)的模就行了,最后再加上一个\(\varphi(q)\),这就是乘方,然后利用快速幂求解。
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll m,p;
ll phimod;
struct juzhen{//矩阵结构体
ll jz[3][3];
ll n,m;
juzhen(){
memset(jz,0,sizeof(jz));
n=0;
m=0;
}
}fib,tmp;
juzhen operator * (juzhen a,juzhen b){//运算符重载
juzhen ans;
ans.n = a.n;
ans.m = b.m;
for(int i=1;i<=a.n;++i){
for(int j=1;j<=b.m;++j){
ans.jz[i][j] = 0;
for(int k=1;k<=a.m;++k){
ans.jz[i][j] = (ans.jz[i][j]%phimod+((a.jz[i][k]%phimod)*(b.jz[k][j]%phimod))%phimod)%phimod;
}
}
}
return ans;
}
void jzksm(ll k){//矩阵快速幂
while(k){
if(k&1){
fib = fib * tmp;
}
tmp = tmp * tmp;
k>>=1;
}
}
ll getphi(ll n){//求欧拉函数值
ll ans = n;
ll m = sqrt(n+0.5);
for(int i=2;i<=m;++i){
if(n%i == 0){
ans = ans/i*(i-1);
while(n%i == 0)n=n/i;
}
}
if(n>1)ans = ans/n*(n-1);
return ans;
}
ll ksm(ll a,ll b,ll mod){//普通快速幂
ll ans = 1;
while(b){
if(b&1){
ans = ans*a%mod;
}
a = a*a%mod;
b>>=1;
}
return ans%mod;
}
int main(){
scanf("%lld%lld",&m,&p);
for(int i=1;i<=m;++i){//初始化
fib.n = 1;
fib.m=2;
fib.jz[1][1] = fib.jz[1][2] = 1;
tmp.n = tmp.m = 2;
tmp.jz[1][1] = tmp.jz[1][2]=tmp.jz[2][1] = 1;
tmp.jz[2][2] = 0;
ll n,q;
scanf("%lld%lld",&n,&q);
phimod = getphi(q);//求出q的欧拉函数值
if(n>=3LL)jzksm(n-2);//n比3大才需要求幂
ll fang = fib.jz[1][1]+phimod;//答案应该是多少次方
ll ans = ksm(p,fang,q);//快速幂
printf("%lld\n",ans);
}
return 0;
}
NO.4 子串
题目描述
有两个仅包含小写英文字母的字符串 \(A\) 和 \(B\)。
现在要从字符串 \(A\) 中取出 \(k\) 个互不重叠的非空子串,然后把这 \(k\)个子串按照其在字符串 \(A\)中出现的顺序依次连接起来得到一个新的字符串。请问有多少种方案可以使得这个新串与字符串 \(B\) 相等?
注意:子串取出的位置不同也认为是不同的方案。
输入格式
第一行是三个正整数 \(n,m,k\),分别表示字符串 \(A\) 的长度,字符串 \(B\) 的长度,以及问题描述中所提到的 \(k\),每两个整数之间用一个空格隔开。
第二行包含一个长度为 \(n\) 的字符串,表示字符串 \(A\)。
第三行包含一个长度为 \(m\) 的字符串,表示字符串 \(B\)。
输出格式
一个整数,表示所求方案数。
由于答案可能很大,所以这里要求输出答案对 100000000710000000071000000007 取模的结果。
输入输出样例
输入 #1
6 3 1
aabaab
aab
输出 #1
2
输入 #2
6 3 2
aabaab
aab
输出 #2
7
输入 #3
6 3 3
aabaab
aab
输出 #3
7
说明/提示
对于第 \(1\) 组数据:\(1\le n\le 500,1\le m\le 50,k=1\);
对于第 \(2\) 组至第 \(3\) 组数据:\(1\le n\le 500,1\le m\le 50,k=2\);
对于第 \(4\) 组至第 \(5\) 组数据:\(1\le n\le 500,1\le m\le 50,k=m\)
对于第 \(1\) 组至第 \(7\) 组数据:\(1\le n\le 500,1\le m\le 50,1\le k\le m\);
对于第 \(1\) 组至第 \(9\) 组数据:\(1\le n\le 1000,1\le m\le 100,1\le k\le m\)
对于所有 \(10\) 组数据:\(1\le n\le 1000,1\le m\le 200,1\le k\le m\)
分析
虎哥的最爱:字符串。
这个题应该是一个\(dp\),机房里的大佬们都用的三维或者四维,我在改题的时候看见了一个二维的,效率挺高的,所以分享一下。我们定义\(f[i][j][k]\)为第二个字符串前\(j\)个字符,第一个字符串里前\(i\)分出来\(k\)段的最大值,因为\(i\)一定是从上一个状态转移来,所以这里可以压一维,然后就是两维,第一维被压掉了。
我们再使用一个数组\(sum[j][k]\)来进行记录,如果上一位的\(s1\)\(s2\)一样,那么\(sum\)每次都可以在转移的时候进行初始化(也算是压行吧):
根据这个三维运算符就可以初始化出来,然后就是转移了,看代码
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1005;
ll f[maxn][maxn];
ll sum[maxn][maxn],n,m,kl;
char s1[maxn],s2[maxn];
int main(){
f[0][0]=1;//初始化
cin>>n>>m>>kl;
cin>>s1>>s2;
for(int i=1;i<=n;++i){
for(int j=m;j>=1;--j){
for(int k=kl;k>=1;k--){
f[j][k] = (f[j][k] + (sum[j][k] = s1[i-1] == s2[j-1] ? sum[j-1][k]+f[j-1][k-1] : 0))%1000000007;//加的时候取模,sum在这里处理,从s2长度-1,段数-1转移而来
}
}
}
cout<<f[m][kl]<<endl;//分成kl段,长度为m的情况
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号