HDU 5961 传递

题目

我们称一个有向图G是 传递的，当且仅当对任意三个不同的顶点a,,若G中有 一条边从a到b且有一条边从b到c ,则G中同样有一条边从a到c。 我们称图G是一个 竞赛图，当且仅当它是一个有向图且它的基图是完全图。换句 话说，将完全图每条边定向将得到一个竞赛图。 下图展示的是一个有4个顶点的竞赛图。

 

 

现在，给你两个有向图P = (V,Ep)和Q = (V,Ee)，满足: 1. EP与Ee没有公共边； 2. (V,Ep⋃Ee)是一个竞赛图。 你的任务是：判定是否P，Q同时为传递的。

Input

包含至多20组测试数据。 第一行有一个正整数，表示数据的组数。 对于每组数据，第一行有一个正整数n。接下来n行，每行为连续的n个字符，每 个字符只可能是’-’,’P’,’Q’中的一种。 ∙如果第i行的第j个字符为’P’，表示有向图P中有一条边从i到j; ∙如果第i行的第j个字符为’Q’，表示有向图Q中有一条边从i到j; ∙否则表示两个图中均没有边从i到j。 保证1 <= n <= 2016，一个测试点中的多组数据中的n的和不超过16000。保证输入的图一定满足给出的限制条件。

Output

对每个数据，你需要输出一行。如果P! Q都是传递的，那么请输出’T’。否则， 请输出’N’ (均不包括引号)。

Sample Input

 4  
4  
-PPP  
--PQ  
---Q  
----  
4  
-P-P  
--PQ  
P--Q  
----  
4  
-PPP  
--QQ  
----  
--Q-  
4  
-PPP  
--PQ  
----  
--Q-  

Sample Output

T
N
T
N

Hint

在下面的示意图中，左图为图为Q。

 

 

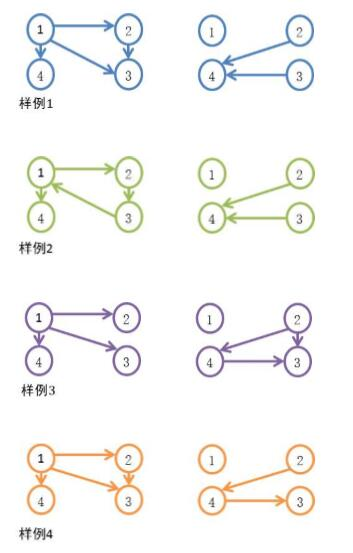
 注：在样例2中，P不是传递的。在样例4中，Q不是传递的。

分析

根据题目中的性质可以知道，这是一个没有环的图

因为这个图是任意两点都直接相连的，所以就可以用BFS找出两点之间的距离，大于一则不是完全图

代码

#include <cstdio>
#include <queue>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 2100;
vector<int> v1[maxn], v2[maxn];
int dis[maxn];
int n, T;
char s[maxn];
bool Bfs(int x, vector<int> v[]){
    queue<int> q;
    memset(dis, 0 , sizeof(dis));
    q.push(x);
    while (q.size()){
        int jl =  q.front();
        q.pop();
        for (int i = 0; i < v[jl].size(); i++){
            int to = v[jl][i];
            if (!dis[to]){
                if (jl != x) return 0;
                dis[to] = dis[jl] + 1;
                q.push(to);
                if (dis[to] > 1) return 0;
            }
        }
    }
    return 1;
}
int main(){
    scanf("%d", &T);
    while (T--){
        scanf("%d", &n);
        for (int i =1; i <= n; i++)
            v1[i].clear(), v2[i].clear();
        for (int i = 1; i <= n; i++){
            scanf("%s", s + 1);
            for (int j = 1; j <= n; j++){
                if (s[j] == 'P') v1[i].push_back(j);
                if (s[j] == 'Q') v2[i].push_back(j);
            }
        }
        bool bj = 1;
        for (int i = 1; i <= n; i++){
            if (!Bfs(i,v1)){
                bj = 0;
                break;
            }
            if (!Bfs(i,v2)){
                bj = 0;
                break;
            }
        }
        if (!bj) printf("N\n");
        else printf("T\n");
    }
    return 0;
}