KMP

简介

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth、J.H.Morris和V.R.Pratt提出，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。

实现

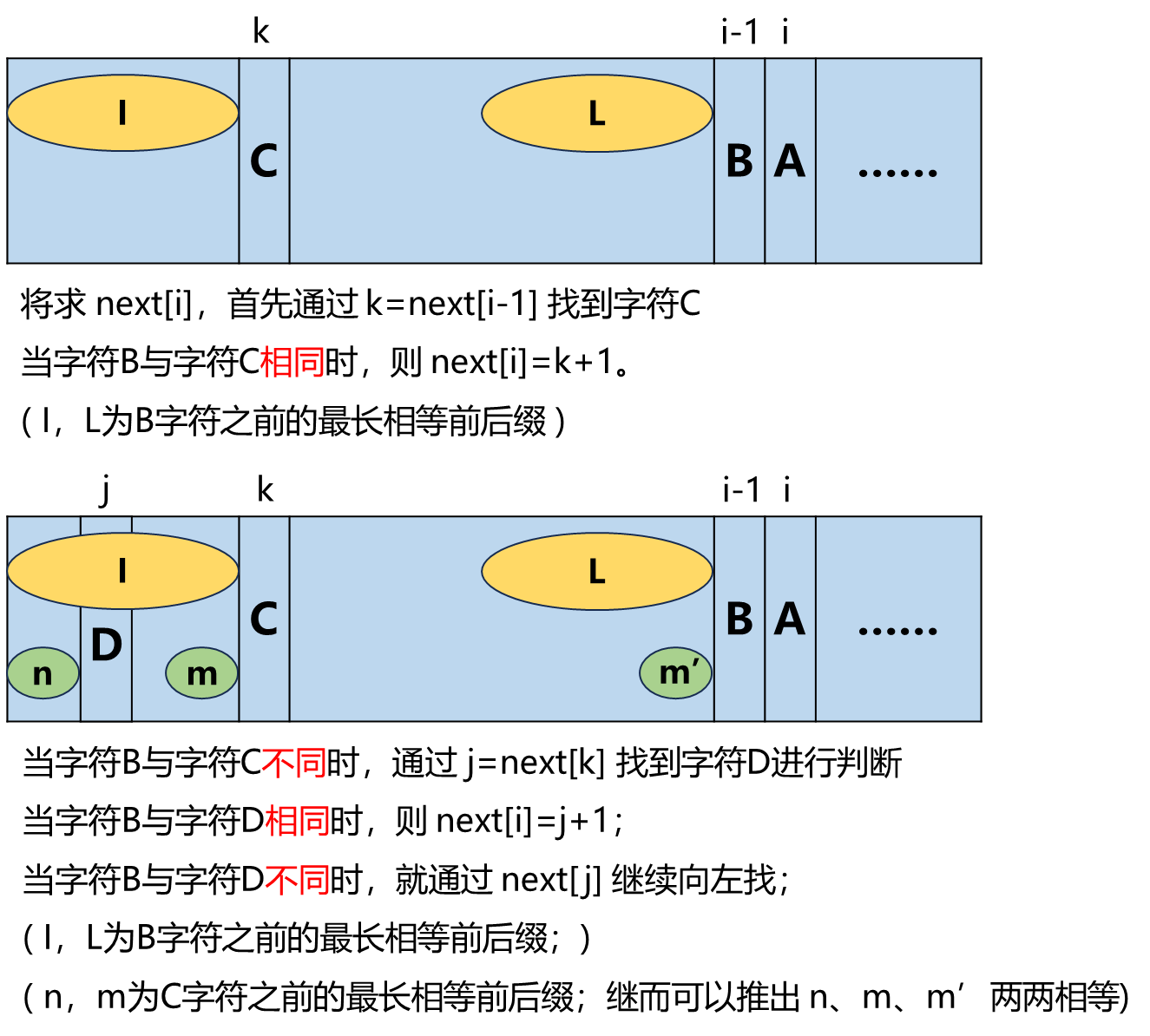
构造 next[] 数组

• 前缀：除最后一个字符外，字符串的所有头部子串

• 后缀：除第一个字符外，字符串的所有尾部子串

• 前后缀相等的最大长度：$\{a, ab, aba\} \cap \{b, ab, bab\}=\{ab\}$

• next[i]：模式串 s[0...i-1] 的相等前后缀的最大长度

字串	前缀	后缀	相等前后缀的最大长度
""	$\phi$	$\phi$	next[0] = -1
"a"	{}	{}	next[1] = 0
"ab"	{"a"}	{"b"}	next[2] = 0
"aba"	{"a", "ab"}	{"a", "ba"}	next[3] = 1
"abab"	{"a", "ab", "aba"}	{"b", "ab", "bab"}	next[4] = 2

匹配

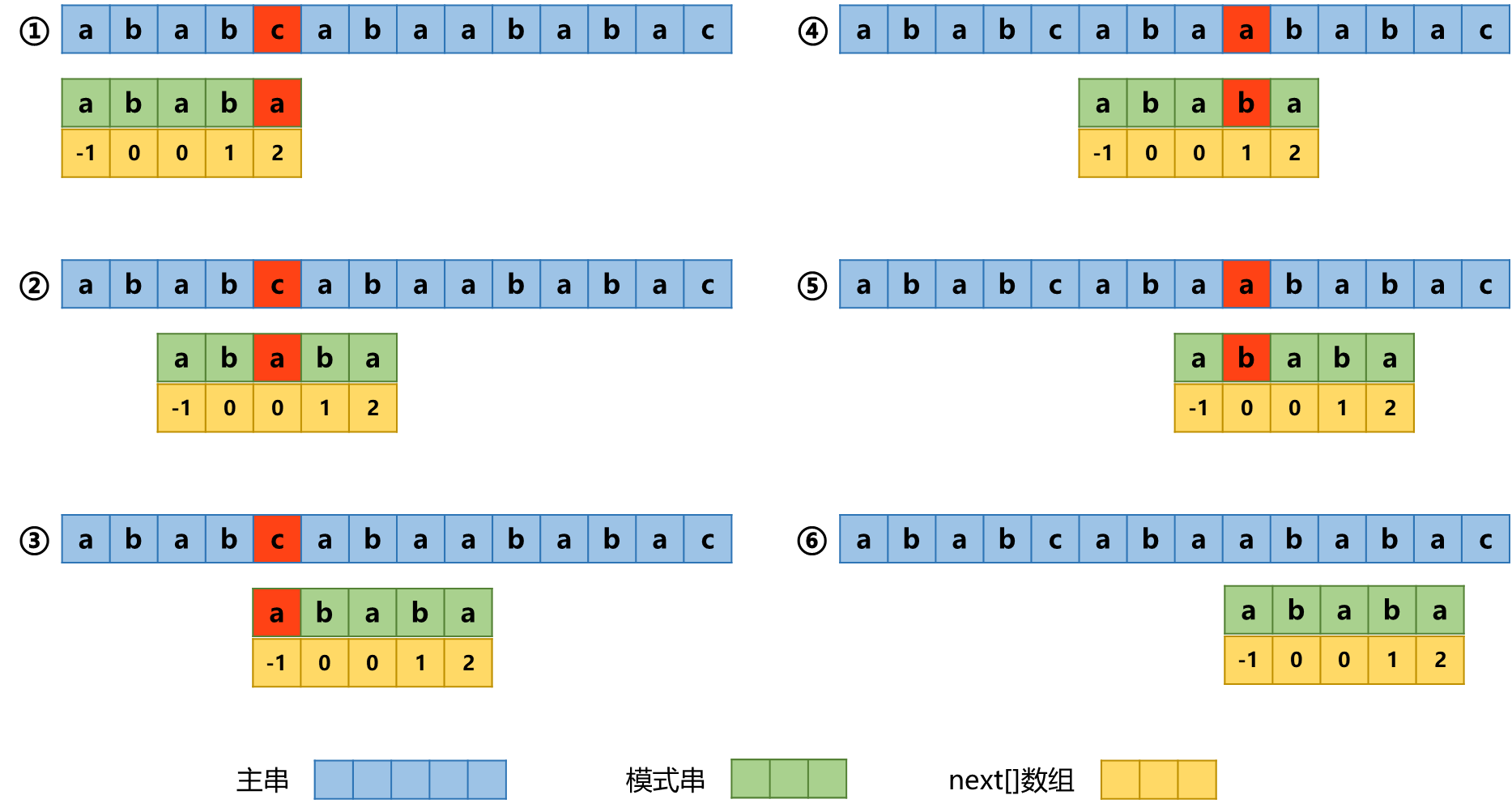
求解 next[] 数组

代码

public class Solution
{
    public static void solution(String s1, String s2)
    {
        ArrayList<Integer> ans = new ArrayList<>();
        int[] next = getNext(s2);
        int i = 0, j = 0;
        while (i < s1.length())
        {
            if (s1.charAt(i) == s2.charAt(j))
            {
                i++;
                j++;
            }
            else if (next[j] == -1) i++;
            else j = next[j];
            if (j == s2.length())
            {
                ans.add(i - j);
                j = 0;
            }
        }
        if (!ans.isEmpty())
            System.out.println(ans.stream().map(String::valueOf).collect(Collectors.joining(" ")));
        else
            System.out.println(-1);
    }

    public static int[] getNext(String s)
    {
        if (s.length() == 1) return new int[]{-1};
        int[] next = new int[s.length()];
        int pos = 2, cn = 0;
        next[0] = -1;
        next[1] = 0;
        while (pos < s.length())
        {
            if (s.charAt(pos - 1) == s.charAt(cn))
                next[pos++] = ++cn;
            else if (cn > 0)
                cn = next[cn];
            else
                next[pos++] = 0;
        }
        return next;
    }

    public static void main(String[] args)
    {
        solution("ababcabaababac", "ababa");
    }
}