Morris二叉树遍历
前言
As we all know，二叉树遍历的方法有递归和利用栈实现的迭代版本，他们的时间和空间复杂度都为 O(n) 。
然而，利用 Morris 遍历方法（利用叶子节点的左右空结点），可以将空间复杂度将为 O(1) ，时间复杂度仍为 O(n) 。
实现
前序遍历
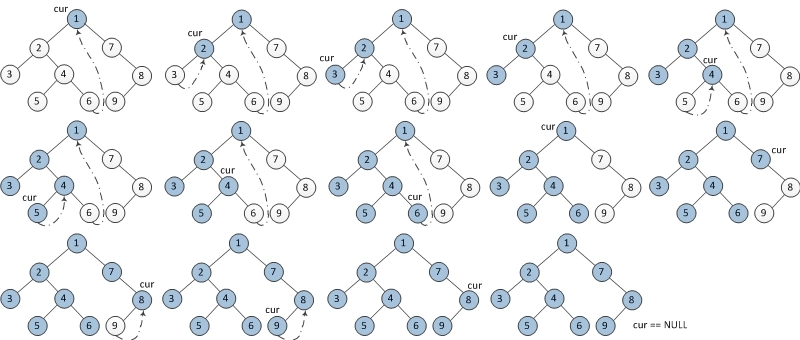
1. 如果当前节点左孩子 cur->left == NULL，输出当前节点的值 cur->value 并将当前结点指向右孩子 cur = cur->right。
2. 如果当前节点左孩子 cur->left != NULL，那么在当前节点的左子树中找出最右叶子结点（即前驱结点 pre ）。
① 如果前驱节点的右孩子 pre->right == NULL ，那么将右孩子指向当前节点（pre->right = cur）。
输出当前节点的值 cur->value。当前节点更新为当前节点的左孩子 cur = cur->left。
② 如果前驱节点的右孩子 pre->right != NULL，即 pre->right = cur。
重新将右孩子设为空 pre->right == NULL。当前节点更新为当前节点的右孩子cur = cur->right。
3. 重复 1、2 直到当前节点为空。
代码
vector<int> preorderTraversal(TreeNode* root)
{
TreeNode* cur = root;
TreeNode* pre = NULL;
vector<int> result;
while(cur!=NULL)
{
if (cur->left == NULL)
{
result.push_back(cur->val);
cur = cur->right;
}
else
{
pre = cur->left;
while(pre->right!=NULL && pre->right!=cur)
{
pre = pre->right;
}
if (pre->right==NULL)
{
pre->right=cur;
result.push_back(cur->val);
cur = cur->left;
}
else
{
pre->right = NULL;
cur = cur->right;
}
}
}
return result;
}
中序遍历
中序遍历与前序遍历相同，输出时机不同而已。
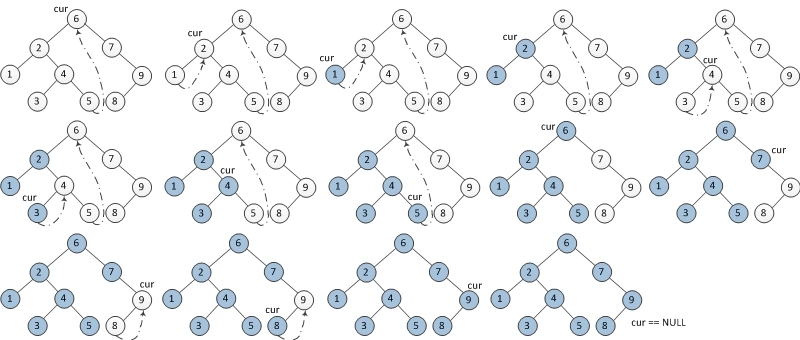
1. 如果当前节点左孩子 cur->left == NULL，输出当前节点的值 cur->value 并将当前结点指向右孩子 cur = cur->right。
2. 如果当前节点左孩子 cur->left != NULL，那么在当前节点的左子树中找出最右叶子结点（即前驱结点 pre ）。
① 如果前驱节点的右孩子 pre->right == NULL ，那么将右孩子指向当前节点（pre->right = cur）。
当前节点更新为当前节点的左孩子 cur = cur->left。
② 如果前驱节点的右孩子 pre->right != NULL，即 pre->right = cur。
重新将右孩子设为空 pre->right == NULL。
输出当前节点的值 cur->value。
当前节点更新为当前节点的右孩子cur = cur->right。
3. 重复 1、2 直到当前节点为空。
代码
vector<int> inorderTraversal(TreeNode* root)
{
TreeNode* cur = root;
TreeNode* pre = NULL;
vector<int> result;
while(cur!=NULL)
{
if (cur->left == NULL)
{
result.push_back(cur->val);
cur = cur->right;
}
else
{
pre = cur->left;
while(pre->right!=NULL && pre->right!=cur)
{
pre = pre->right;
}
if (pre->right == NULL)
{
pre->right=cur;
cur = cur->left;
}
else
{
pre->right = NULL;
result.push_back(cur->val);
cur = cur->right;
}
}
}
return result;
}
后序遍历
1. 新增临时结点dump，并且将 root 设为 dump 的左孩子。
2. 如果当前节点左孩子 cur->left == NULL，输出当前节点的值 cur->value 并将当前结点指向右孩子 cur = cur->right。
3. 如果当前节点左孩子 cur->left != NULL，那么在当前节点的左子树中找出最右叶子结点（即前驱结点 pre ）。
① 如果前驱节点的右孩子 pre->right == NULL ，那么将右孩子指向当前节点（pre->right = cur）。
当前节点更新为当前节点的左孩子 cur = cur->left。
② 如果前驱节点的右孩子 pre->right != NULL，即 pre->right = cur。
逆序输出当前结点左孩子到前序结点的路径。
重新将右孩子设为空 pre->right == NULL。当前节点更新为当前节点的右孩子cur = cur->right。
4. 重复 2、3 直到当前节点为空。
代码
vector<int> postorderTraversal(TreeNode* root)
{
TreeNode dump(-1);
dump.left = root;
TreeNode* cur = &dump;
TreeNode* pre = NULL;
vector<int> result;
while(cur!=NULL)
{
if (cur->left == NULL)
{
cur = cur->right;
}
else
{
pre = cur->left;
while(pre->right!=NULL && pre->right!=cur)
{
pre = pre->right;
}
if (pre->right == NULL)
{
pre->right=cur;
cur = cur->left;
}
else
{
printReverse(cur->left, pre, result);
pre->right = NULL;
cur = cur->right;
}
}
}
return result;
}
void printReverse(TreeNode* from, TreeNode* to, vector<int>& result) //输出单链表
{
Reverse(from, to);
TreeNode* p = to;
while(true)
{
result.push_back(p->val);
if(p == from)
{
break;
}
p = p->right;
}
Reverse(to, from);
}
void Reverse(TreeNode* from, TreeNode* to) //翻转单链表
{
TreeNode* x = from;
TreeNode* y = from->right;
TreeNode* z;
if (from == to)
{
return;
}
x->right = NULL;
while(x != to)
{
z = y->right;
y->right = x;
x = y;
y = z;
}
}
总结
通过三种遍历可以看到，其实总体上的代码逻辑没有发生改变，主要是改变了输出结果的时机和方式。
