LCA —— 最近公共祖先
# 定义
给定一棵有根树,若结点 z 既是结点 x 的祖先,也是结点 y 的祖先,则称 z 是x,y的公共祖先。
在 x,y 的所有公共祖先中,深度最大的一个称为 x,y 的最近公共祖先,记为LCA(x,y)。
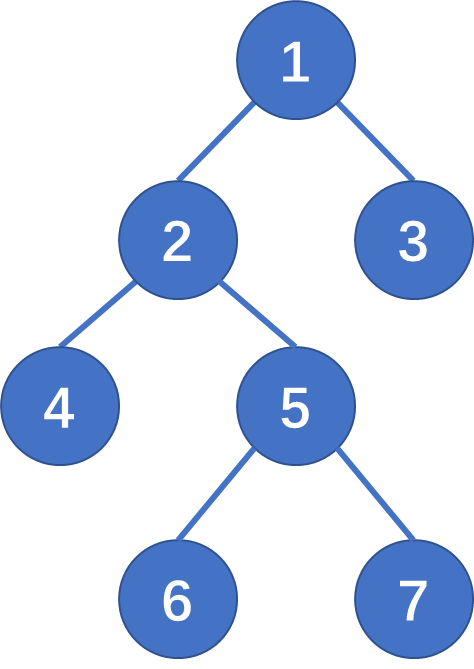
LCA(4 , 7) = 2,LCA(6,7) = 5
# 实现
## 暴力大法好
若求LCA(4 , 7),分别求 4 和 7 到根节点的路径。
4 -> root 的路径为:4 -> 2 -> 1。
7 -> root 的路径为:7 -> 5 -> 2 -> 1。
那么在两个路径中共有的第一个点即为答案。
所以LCA(4 , 7) = 2。
暴力大法比较简单也不怎么常用,不过多介绍。
## Tarjan
伪代码
Tarjan(u)//marge和find为并查集合并函数和查找函数
{
for each(u,v) //访问所有u的子节点v
{
Tarjan(v); //继续往下遍历
marge(u,v); //合并v到u上
标记 v 被访问过;
}
for each(u,e) //访问所有和u有询问关系的e
{
如果e被访问过;
u,e的最近公共祖先为find(e);
}
}
通过伪代码可以看出通过 dfs 从上往下遍历时,利用 dfs 的特性,并查集从下往上维护,从而找到LCA( )。
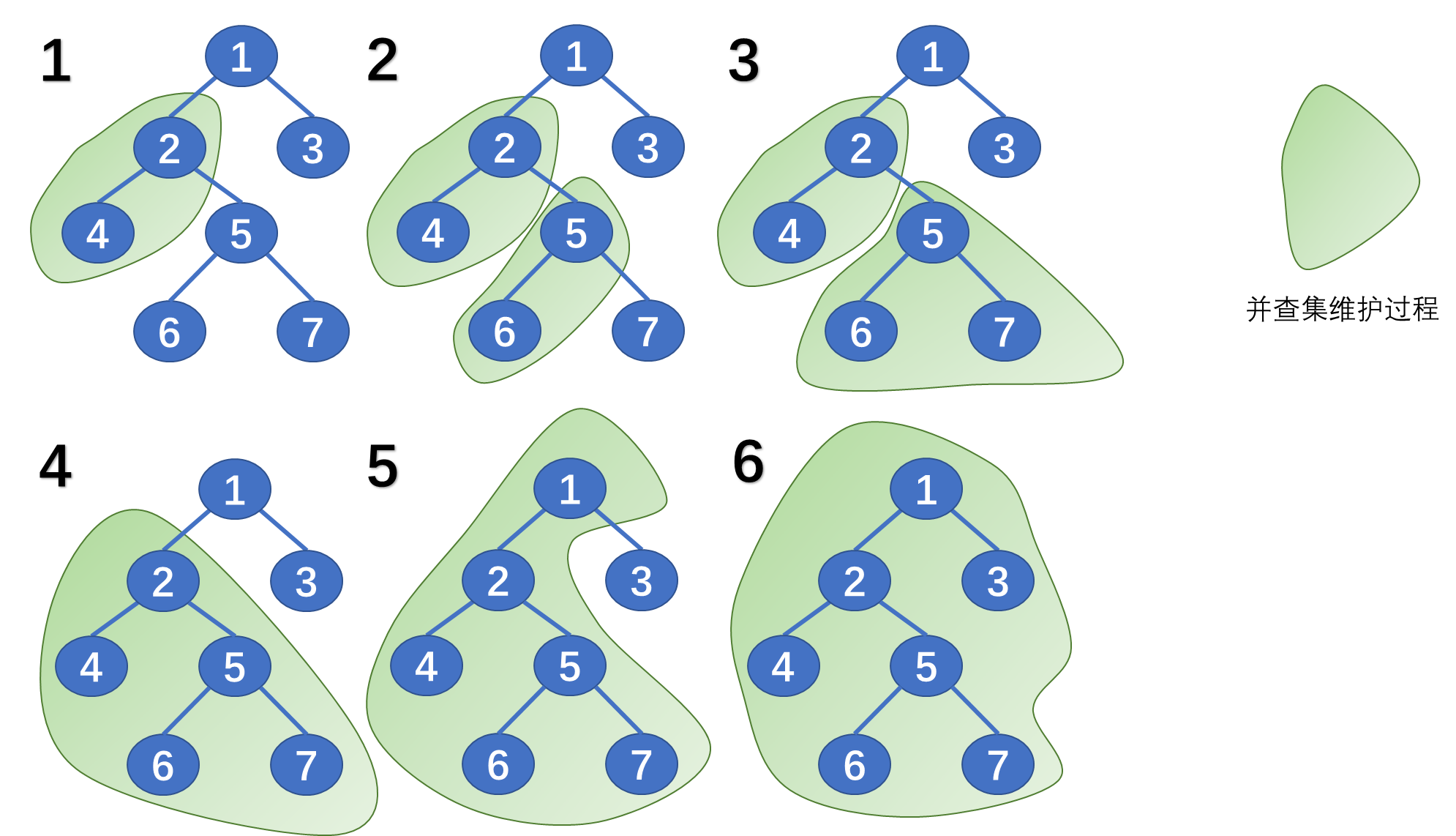
通过并查集维护如何得到 LCA 呢?
以图2为例,图2的状态为 Tarjan 函数已经执行到 7 结点,并查集的维护范围如绿色区域所示,那么就可以得到 LCA(7 , 6) = 5,LCA(7 , 4) = 2,LCA(7 , 2) = 2等信息。
因为 DFS 的特性,当访问与结点 7 有询问关系的结点6,4,2 时,若结点被标记(访问)过,那么并查集已经维护了这个结点,所以find(6) = 5,find(4) = 2,find(2) = 2。
通过伪代码可以看出,求解 LCA 的过程,都是在 dfs 的同时求得的,所以这是个离线算法。🙃
## ST
这个算法就是在线算法了。🐶
暴力大法的思路为一个一个结点进行比较,直到找到最近公共祖先为止。
因为暴力大法逐个进行查找(即幅度为 1) ,这样导致了不好的效果,但是它提供了一种思路。
那么我们可以将查找的幅度变为 (即幅度为 1,2,4,8,16,32),这样就会极大加快向上寻找最近公共结点的速度。
为什么要选择 作为查找的幅度,因为
,都可以由
组合出来。
🔰 举个栗子
## 预处理
//deep[x] 结点 x 的深度;
//fa[x][y] 结点 x 的第 2^y 个祖先
void getdeep(int now,int father) //now表示当前节点,father表示它的父亲结点
{
deep[now]=deep[father]+1;
fa[now][0]=father;
//意思是f的2^i祖先等于f的2^(i-1)祖先的2^(i-1)祖先
//2^i=2^(i-1)+2^(i-1)
for(int i=1;(1<<i)<=deep[now];i++)
fa[now][i]=fa[fa[now][i-1]][i-1];
for(int i=head[now];i;i=edge[i].next)
{
if(edge[i].to==father)continue;
getdeep(edge[i].to,now);
}
}
利用 dfs 记录deep[] 和 fa[][]。deep[x]为结点 x 的深度,即搜索的深度。fa[x][y]为结点 x 的第 2^y 的祖先,等价于结点 x 的第 2^(y-1) 个祖先的第2^(y-1)个祖先,即fa[x][y] = fa[x 结点的第 2^(y-1) 个祖先][第 2^(y-1) 个祖先] = fa[fa[x][y-1]][y-1]。
在预处理之后,我们就得到了每个结点的深度(deep[])和每个结点的第2^0,2^1,2^2,2^3个祖先(fa[][])。
## 求解
求解的步骤为先把两个点提到同一高度,再统一开始跳。
int lca(int u,int v)
{
if(deep[u]!=deep[v])
{
if(deep[u]<deep[v]) swap(u,v); //默认 u 的深度比 v 大
for(int i=19;i>=0;i--) //使 u 的深度跳到 v 的深度
{
if(deep[st[u][i]]>=deep[v])
u=st[u][i];
}
}
if(u==v) return u;
for(int i=19;i>=0;i--) //现在 u 和 v 的深度相同,然后一起向上直到找到最近公共祖先的孩子
{
if(st[u][i]!=st[v][i])
{
u=st[u][i];
v=st[v][i];
}
}
return st[u][0]; //返回lca(u,v)
}
提到同一高度:
若 u,v 的深度不同,则将深度大的结点变化到深度小的深度。
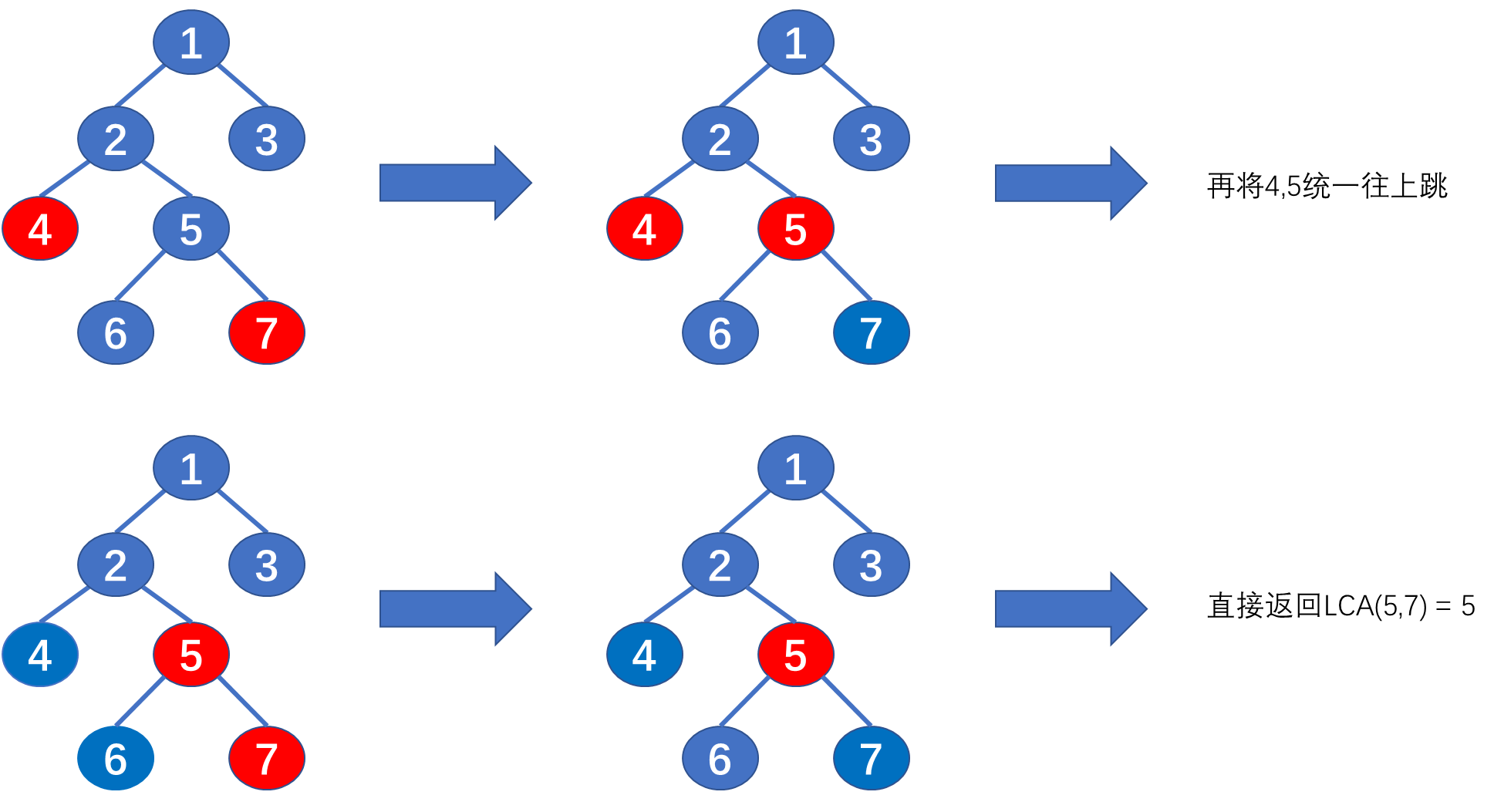
深度大的结点肯定可以变化到深度小的深度。因为深度差是一个定值,所以可以用若干个2的幂次方进行组合达到这个深度。
我们发现 i(第2^i个祖先结点)是从大到小进行遍历的,因为这样才能够正好凑齐一个定值。
🔰 举个栗子
用 1,2,4来组成 5 。
如果从小到大进行遍历,可能会出现类似于“回溯”的现象:① 5 > 1,② 5 > 1 + 2,③ 5 < 1 + 2 + 4,④ ”回溯“,⑤ 5 = 1 + 4 。
然而从大到小遍历就不会出现这种问题:① 5 > 4,② 因为 5 > 4 +2,所以不选 2,③ 5 = 4 + 1 。可以看出,只要是选了这个数,那么这个数肯定是答案的一部分。
统一开始跳:
现在 u , v 的深度相同,令深度分别为deep_u , deep_v(deep_u == deep_v),u , v 的最近公共祖先为 lca ,深度为 deep_lca(deep_lca < deep_u)。
我们可以看出,深度小于 deep_lca 的那些层,每层肯定会有一个结点是 u , v 的祖结点(只不过不是最近公共祖先罢了),所以我们必须找到最近公共祖先的孩子结点,那么孩子结点的父节点就是 u,v 的最近公共祖先。这样才能保证找到的这个结点是祖先的同时还是最近的。
所以我们利用 st[u][i] != st[v][i] 让 u,v 的深度不断向上更新,深度达到deep_lca + 1 为止。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· winform 绘制太阳,地球,月球 运作规律
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 上周热点回顾(3.3-3.9)
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」