线段树

定义

线段树是常用来维护区间信息的数据结构。

线段树可以在$O(logN)$的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值)等操作。

实现

以数组 arr{9,3,-1,8,4,-2} 为例 (下标从 1 开始）

存储

//区间[L,R], w表示维护的数据, lazy为懒惰标记。
struct node
{
 int L,R,w,lazy;
}tree[maxn];

建树

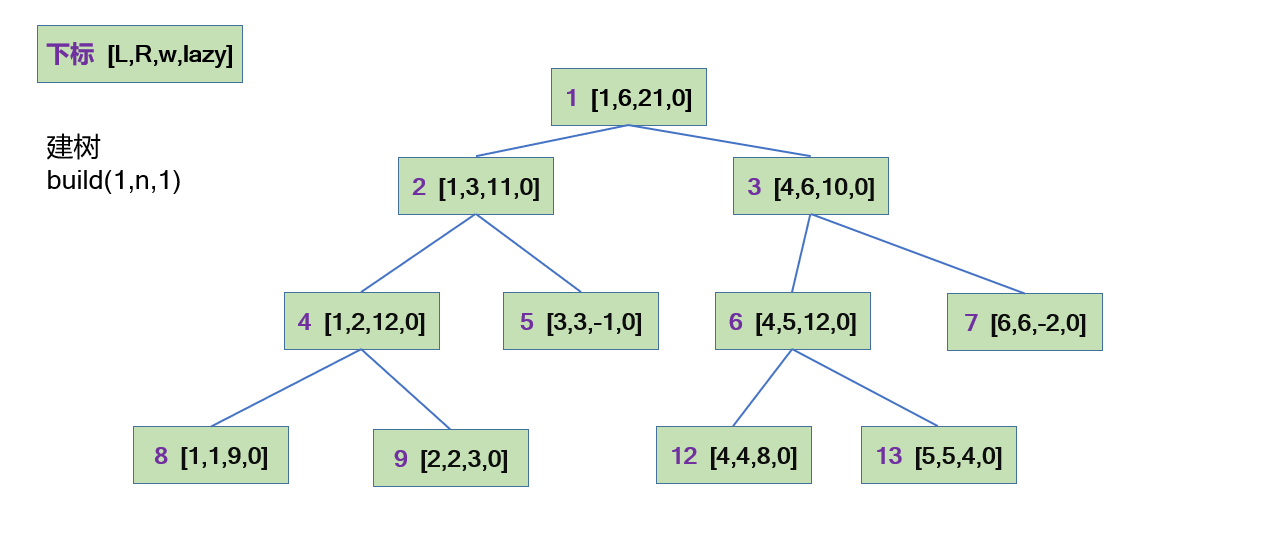
void build(int L,int R,int k)   
{
  tree[k].L=L; tree[k].R=R; tree[k].lazy=0;
  if(tree[k].L==tree[k].R)
  {
    scanf("%d",&tree[k].w);
    return;
  }
  int m=(L+R)/2;
  build(L,m,k*2);
  build(m+1,R,k*2+1);
  tree[k].w=tree[k*2].w+tree[k*2+1].w;
}

单点查询

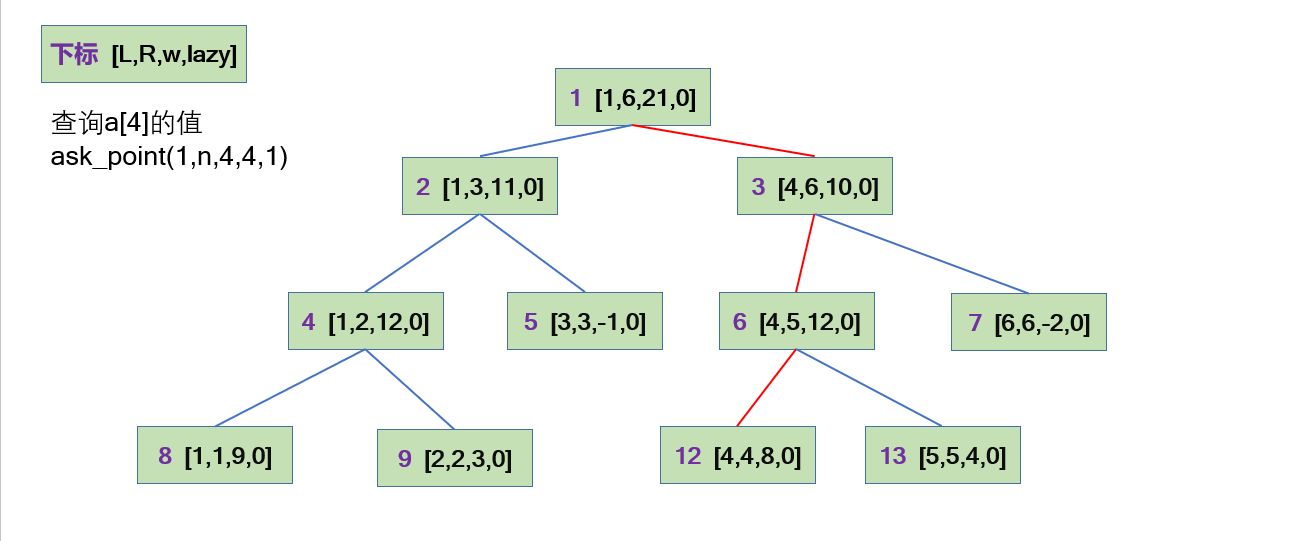
void ask_point(int L,int R,int l,int r,int k)
{
  if(tree[k].L==tree[k].R)
  {
    printf("%d",tree[k].w);
    return ;
  }
  if(tree[k].lazy) down(k);
  int m=(L+R)/2;
  if(l<=m) ask_point(L,m,l,r,k*2);
  else ask_point(m+1,R,l,r,k*2+1);
}

单点修改

void change_point(int L,int R,int l,int r,int k,int add)
{
  if(tree[k].L==tree[k].R)
  {
    tree[k].w+=add;
    return;
  }
  if(tree[k].lazy) down(k);
  int m=(L+R)/2;
  if(l<=m) change_point(L,m,l,r,k*2,add);
  else change_point(m+1,R,l,r,k*2+1,add);
  tree[k].w=tree[k*2].w+tree[k*2+1].w; 
}

区间查询

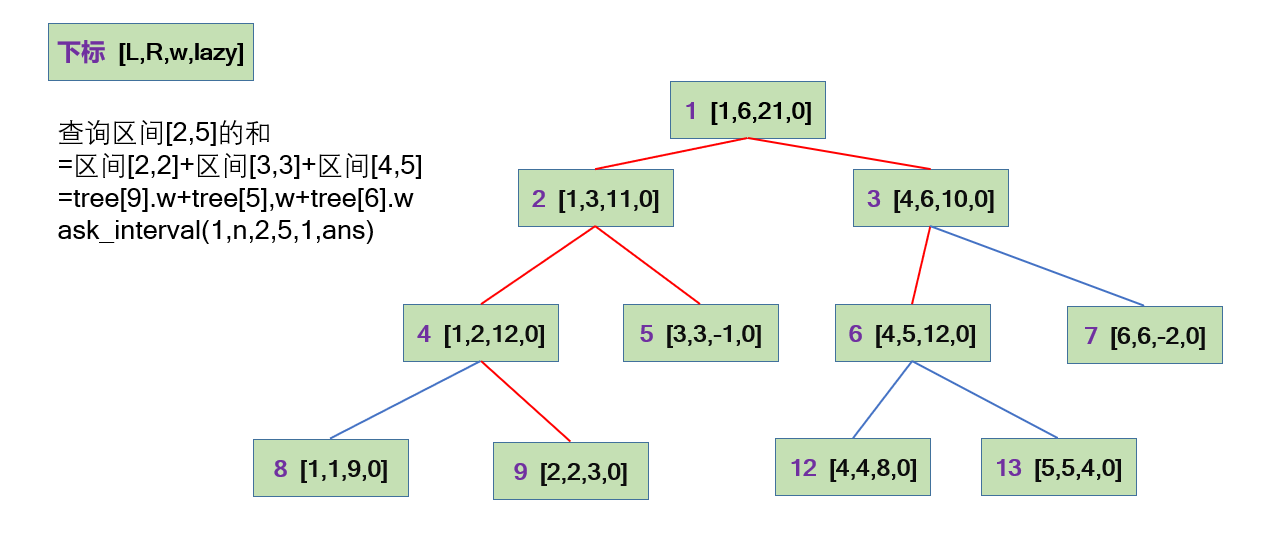
void ask_interval(int L,int R,int l,int r,int k,int &ans) 
{
  if(tree[k].L>=l&&tree[k].R<=r) 
  {
    ans+=tree[k].w;
    return;
  }
  if(tree[k].lazy) down(k);
  int m=(L+R)/2;
  if(l<=m) ask_interval(L,m,l,r,k*2,ans);
  if(r>m) ask_interval(m+1,R,l,r,k*2+1,ans);
}

区间修改

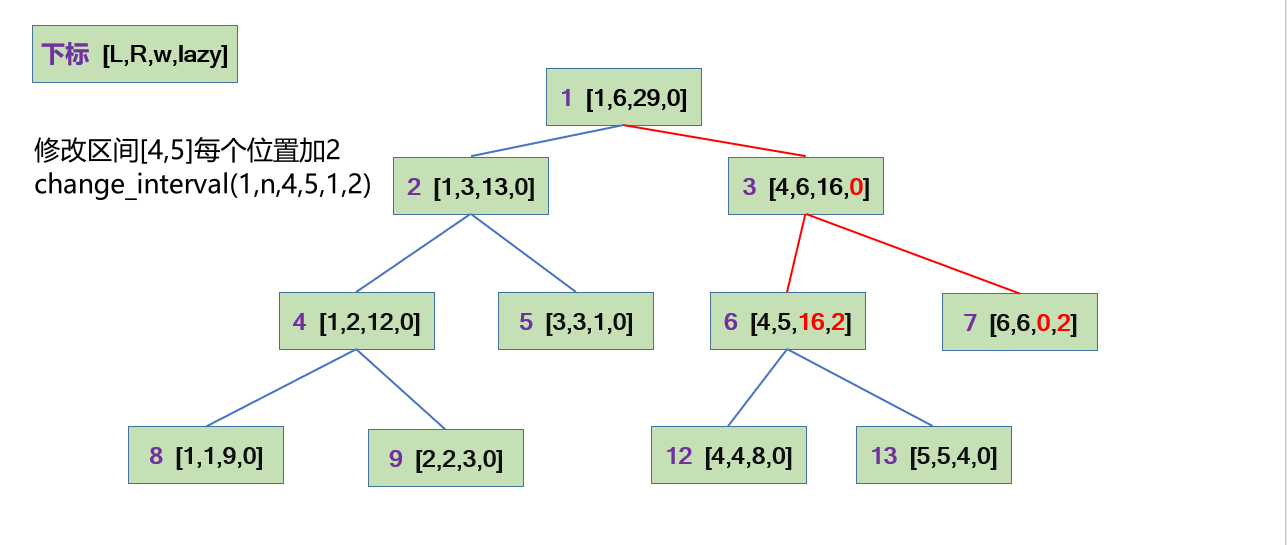
void change_interval(int L,int R,int l,int r,int k,int add) 
{
  if(tree[k].L>=l&&tree[k].R<=r)
  {
    tree[k].w+=(tree[k].R-tree[k].L+1)*add;
    tree[k].lazy+=add;
    return;
  }
  if(tree[k].lazy) down(k);
  int m=(L+R)/2;
  if(l<=m) change_interval(L,m,l,r,k*2,add);
  if(r>m) change_interval(m+1,R,l,r,k*2+1,add);
  tree[k].w=tree[k*2].w+tree[k*2+1].w;
}

下传函数

void down(int k) 
{
  tree[k*2].lazy+=tree[k].lazy;
  tree[k*2+1].lazy+=tree[k].lazy;
  tree[k*2].w+=tree[k].lazy*(tree[k*2].R-tree[k*2].L+1);
  tree[k*2+1].w+=tree[k].lazy*(tree[k*2+1].R-tree[k*2+1].L+1);
  tree[k].lazy=0;
}