hdu 5950 Recursive sequence

Recursive sequence

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 5120    Accepted Submission(s): 2197

Problem Description

  Farmer John likes to play mathematics games with his N cows. Recently, they are attracted by recursive sequences. In each turn, the cows would stand in a line, while John writes two positive numbers a and b on a blackboard. And then, the cows would say their identity number one by one. The first cow says the first number a and the second says the second number b. After that, the i-th cow says the sum of twice the (i-2)-th number, the (i-1)-th number, and i^4. Now, you need to write a program to calculate the number of the N-th cow in order to check if John’s cows can make it right. 

 

Input

The first line of input contains an integer t, the number of test cases. t test cases follow.
Each case contains only one line with three numbers N, a and b where N,a,b <2^31 as described above.

 

Output

For each test case, output the number of the N-th cow. This number might be very large, so you need to output it modulo 2147493647.

 

Sample Input

2 3 1 2 4 1 10

 

Sample Output

85 369

 

题意：T组数据。每组数据有N，F[1]=a,F[2]=b,F[N]=2*F[N-1]+F[N-2]+n^4,求F[N]。

 

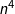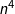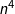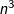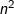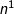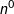题解：矩阵构造。先把处理一下，，完成了由到的转换。利用F[1]，F[2]，，，，，构造矩阵。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

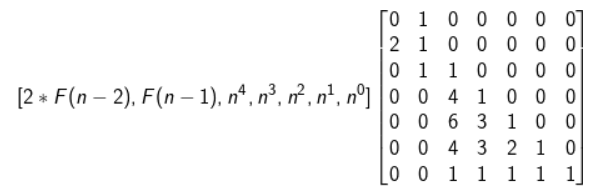
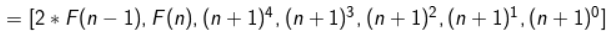
代码：

#include<bits/stdc++.h>
using namespace std;
const long long mod=2147493647;
struct node
{
  long long Martix[7][7];
  node operator *(const node&n) const
  {
    int i,j,k;node sum;
    for(i=0;i<7;i++)
     for(j=0;j<7;j++)
      {
        sum.Martix[i][j]=0;
        for(k=0;k<7;k++) 
          sum.Martix[i][j]=(sum.Martix[i][j]+Martix[i][k]*n.Martix[k][j])%mod;
      }
    return sum;
  }
};
int main()
{
  long long T,n,a,b;
  node A,B,ans;
  scanf("%ld",&T);
  while(T--)
  {
    scanf("%lld%lld%lld",&n,&a,&b);
    fill(A.Martix[0],A.Martix[0]+49,0);
    fill(B.Martix[0],B.Martix[0]+49,0);
    fill(ans.Martix[0],ans.Martix[0]+49,0);
    for(int i=0;i<7;i++) A.Martix[i][i]=B.Martix[i][i]=1;
    
    ans.Martix[0][0]=2*a%mod;ans.Martix[0][1]=b%mod;
    ans.Martix[0][2]=81;ans.Martix[0][3]=27;
    ans.Martix[0][4]=9;ans.Martix[0][5]=3;ans.Martix[0][6]=1;
    
    B.Martix[0][0]=0;B.Martix[0][1]=1;B.Martix[1][0]=B.Martix[5][4]=2;
    B.Martix[2][1]=B.Martix[6][2]=B.Martix[6][3]=B.Martix[6][4]=B.Martix[6][5]=1;
    B.Martix[3][2]=B.Martix[5][2]=4;
    B.Martix[4][2]=6;
    B.Martix[4][3]=B.Martix[5][3]=3;
  
    n-=2;
    while(n)
    {
       if(n&1) A=A*B;
       n>>=1;
       B=B*B;
    }
    ans=ans*A;
    printf("%lld\n",ans.Martix[0][1]%mod);
  }
  system("pause");
  return 0;
}