偏差和方差以及偏差方差权衡(Bias Variance Trade off)
当我们在机器学习领域进行模型训练时,出现的误差是如何分类的?
我们首先来看一下,什么叫偏差(Bias),什么叫方差(Variance):
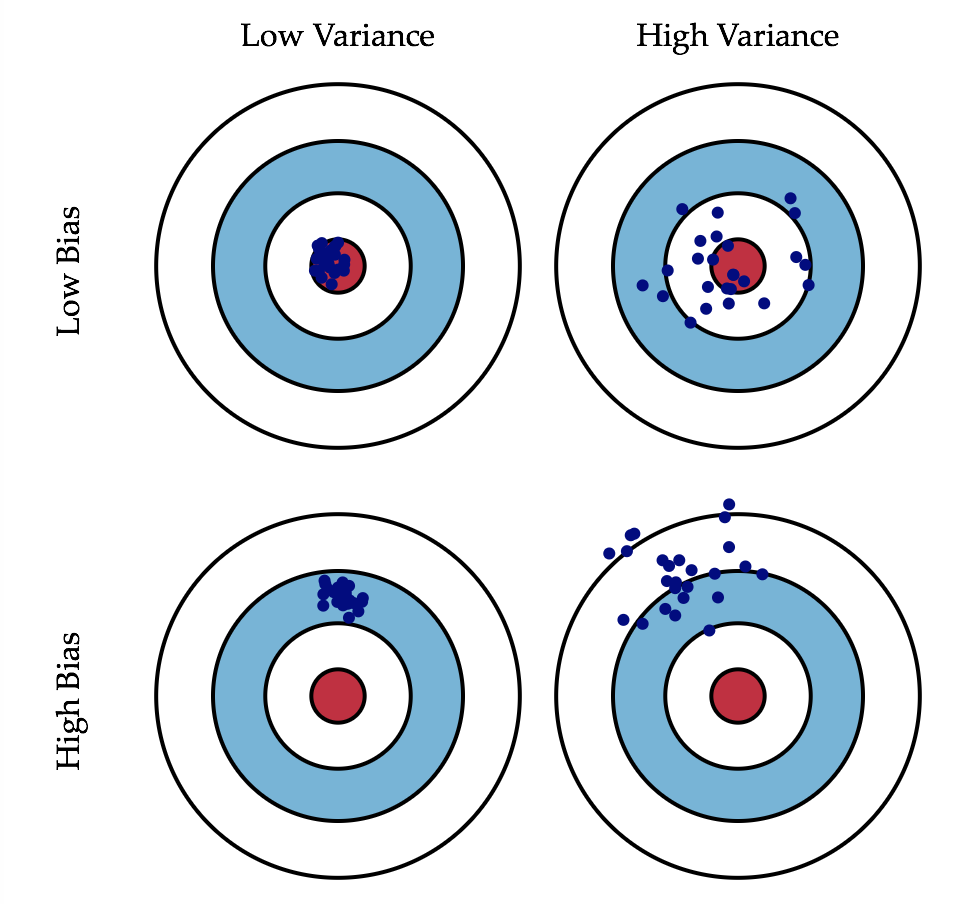
这是一张常见的靶心图
可以看左下角的这一张图,如果我们的目标是打靶子的话,我们所有的点全都完全的偏离了这个中心的位置,那么这种情况就叫做偏差
再看右上角这张图片,我么们的目标是右上角这张图片中心的红色位置,我们射击的点都围绕在这个红色的点的周围,没有大的偏差,但是各个点间过于分散不集中,就是有非常高的方差
我们进行机器学习的过程中，大家可以想象，我们实际要训练的那个模型都是要预测一个问题，这个问题本身我们就可以理解成是这个靶子的中心，而我们根据数据来拟合一个模型，进而预测这个问题，我们拟合的这个模型其实就是我们打出去的这些枪，那么我们的模型就有可能犯偏差和方差这样两种错误
一般来说我们说我们训练一个模型，这个模型会有误差，这个误差通常来源于三方面 :
模型误差 = 偏差(Bias) + 方差(Variance) + 不可避免的误差
不可避免的误差: 客观存在的误差,例如采集的数据的噪音等,是我们无法避免的
偏差和方差这两个问题只是和我们的算法和我们训练的模型相关的两个问题，也就是说我们训练一个模型它有偏差，主要的原因就在于我们很有可能对这个问题本身的假设是不正确的，那么最典型的例子就是,如果我们针对非线性的数据或者说是非线性的问题，使用诸如线性回归这种现象的方法的话，那显然会产生非常高的偏差，那么在我们现实的环境中欠拟合(underfitting)就是这样的一个例子.
还有典型的一个例子就是你训练数据所采用的那个特征，其实跟这个问题完全没有关系，比如说我们想预测一个学生的考试成绩，但是呢，我们是用这个学生的名字来预测他的考试成绩，那么显然一定是高偏差的，因为这个特征本身离我们要预测的那个问题的目标考试成绩之间是高度不相关的
方差在机器学习的过程中它的表现就在于数据的一点点的扰动都会极大的影响我们的模型，换句话说我们的模型没有完全的学习到这个问题的实质这个中心而学习到了很多的噪音，通常来讲我们的模型具有较高的方差的原因是我们的模型太过复杂，比如说高阶多项式回归这样的例子，过拟合(overfitting)就会极大的引入方差
- 有一些算法天生是高方差的算法。如kNN,决策树等
- 非参数学习通常都是高方差算法。因为不对数据进行任何假设
- 有一些算法天生是高偏差算法。如线性回归
- 参数学习通常都是高偏差算法。因为堆数据具有极强的假设
大多数算法具有相应的参数,可以调整偏差和方差, 比如kNN中的k和线性回归中使用多项式回归。
偏差和方差通常是矛盾的,我们要在两者之间找到一个平衡
在机器学习领域,主要的挑战来自方差,当然主要是在算法方面,实际问题中原因不尽相同
解决高方差的通常手段:
1.降低模型复杂度
2.减少数据维度;降噪
3.增加样本数
4.使用验证集
5.模型正则化
