后缀数组做题笔记
后缀数组笔记
这里挂一个学弟学习笔记的链接:Link ,大部分内容都学习自这里。
按道理这篇文章会持续更新
1.Preface
首先有几个概念需要明确。本文中所有字符串下标从 \(1\) 开始,\(\rm LCP\) 表示最长公共前缀。
2.Basic
后缀数组基本操作就不说了,可以到其他地方学习。这里只放一个板子。
char s[DMAX];
int x[DMAX],y[DMAX],c[DMAX];
int sa[DMAX],rnk[DMAX],h[DMAX];
// sa 排名为i的后缀编号是什么
// rnk 编号为i的后缀排名是什么
// height 排名为i和i-1的LCP
void SA(int n,int m){ //n 长度 m 最开始为字符集大小
for(int i=1;i<=n;i++) x[i]=s[i],c[x[i]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i>=1;i--) sa[c[x[i]]--]=i;
m=0;
for(int p=1;m<n;p<<=1){
m=0;
for(int i=n-p+1;i<=n;i++) y[++m]=i;
for(int i=1;i<=n;i++){
if(sa[i]>p){
y[++m]=sa[i]-p;
}
}
for(int i=1;i<=m;i++) c[i]=0;
for(int i=1;i<=n;i++) c[x[i]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i>=1;i--) sa[c[x[y[i]]]--]=y[i];
for(int i=1;i<=n;i++) y[i]=x[i],x[i]=0;
x[sa[1]]=1,m=1;
for(int i=2;i<=n;i++){
if(y[sa[i]]==y[sa[i-1]] && y[sa[i]+p]==y[sa[i-1]+p]){
x[sa[i]]=m;
}
else{
x[sa[i]]=++m;
}
}
}
for(int i=1;i<=n;i++){
rnk[sa[i]]=i;
}
for(int i=1;i<=n;i++){
h[rnk[i]]=h[rnk[i-1]]-1;
if(h[rnk[i]]<0){
h[rnk[i]]=0;
}
while(s[i+h[rnk[i]]]==s[sa[rnk[i]-1]+h[rnk[i]]]){
h[rnk[i]]++;
}
}
}
/*
1.不要把两个 m=0 少写了
2.注意 x,y 数组表示的是排序顺序,在求新的 x 数组的地方,不要把 sa 和 x,y 写反了
3.求 rnk 数组的时候注意 while 循环里面的下标
4.所有数组的大小都应该至少为字符串长度
*/
首先是一些定义:\(\rm LCP(i,j)\) 表示 \(sa_i\) 和 \(sa_j\) 这两个后缀的最长公共前缀。
一些性质还是在这里列举一下(还是很重要的):
- \(\rm LCP(i,j)=\rm LCP(j,i)\)
- \(\rm LCP(i,j)=\min\limits_{i\le k \le j} \rm \{LCP(i,k),\rm LCP(k,j) \}\)
- \(\rm LCP(i,j)=\min\limits_{i<k \le j} \{ LCP(k-1,k) \}\)
最后一条性质直接阐述了 \(h\) 数组的用途,两个后缀的 \(\rm LCP\) 就是他们位置之间 \(h\) 的最小值。
3.Usage
1.LG4051
后缀数组基本应用,相当于求最小表示法。直接把字符串复制一遍接在原串后面,然后做 SA 。从左到右扫描整个 \(sa\) 数组,每遇到一个 \(sa\) 值小于原串长度的就可以得到一个答案的字符。
复杂度是 \(\mathcal O(n\log n)\)
2.UVA1223
题意就是查询最长的至少出现两次的子串。首先所有的子串都可以看作一个后缀的前缀。对于每一个后缀,和他拥有最大 \(\rm LCP\) 的另一个后缀一定和它相邻,也就是 \(h\) 数组所表示的内容。所以只要对所有 \(h\) 取 \(\max\) 就可以得到答案了。
复杂度是 \(\mathcal O(n\log n)\)
3.LG2852
题意即是求出现至少 \(k\) 次的最长子串。显然考虑最长子串时,我们只需考虑 \(h\) 中所有长度为 \(k\) 的区间的区间最小值,这表明了对于这个区间内所有的后缀而言都存在一个这么长的相同前缀(也是极大相同前缀)。取所有区间中最大的哪个即可。写一个 \(ST\) 表就可以实现 \(\mathcal O(1)\) 查询。
复杂度是 \(\mathcal O(n\log n)\)
4.LG2408
求字符串中本质不同子串个数。考虑两个后缀的所有前缀,他们重复的子串个数就是他们的 \(\rm LCP\) 。于是我们只要把这部分减掉就可以很容易的算出来答案了。
那么答案就是:\(\sum\limits_{i=1}^n (n-sa_i+1)-h_i\)
复杂度是 \(\mathcal O(n\log n)\)
5.LG1117
\(95pts\) 部分是很好写的,对于每个点我们计算出来 \(f,g\) 表示以这个点开始的 \(AA\) 串个数和以这个点结束的 \(AA\) 串个数。答案就是 \(\sum\limits_{i=1}^{n-1} f_{i+1}\times g_i\)。 可以用哈希以 \(\mathcal O(n^2)\) 的时间复杂度轻松通过。
正解的话,我们还是考虑计算 \(f,g\) 。我们先枚举 \(A\) 的长度 \(len\) ,我们标记所有 \(A\) 的倍数的点。那么每一个 \(AA\) 串都会穿过两个标记点。
我们记两个标记点分别为 \(i,j\) ,那么有 \(i+len=j\) 。记 \(Lcp=\rm LCP(i,j)\) ,\(Lcs=\rm LCS(i-1,j-1)\) 。我们尝试计算两个标记点对答案的贡献。(这里 \(Lcp\) 要对 \(len\) 取 \(\min\) ,\(Lcs\) 要对 \(len-1\) 取 \(\min\) )
如果有 \(Lcp+Lcs < len\) 那么就无法构成 \(AA\) 串。反之我们可以得到 \(AA\) 串,且合法的左端点(右端点)是一段连续的区间,差分统计 \(f,g\) 即可。(合法的区间长度为 \(Lcp+Lcs-len+1\) )。具体可以参考代码。结合下图可能会更好的理解。
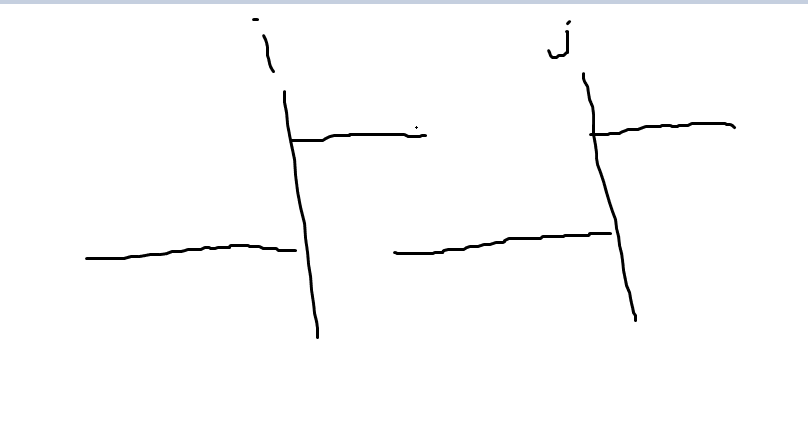
这里我们没聚了所有的长度,且相当于考虑每个长度的所有倍数,所以这一部分复杂度是 \(\mathcal O(n\ln n)\) 。
总复杂度是 \(\mathcal O(n\log n+n\ln n)\) 。
注意下多测清空问题,所有数组(基本上)做完一次都要清空,SA需要的东西做完就清空,不要等到下一次做之前清空。
6.LG6640
其实这道题应该也可以使用后面 LG4094 的做法来做,但是这个做法就这道题而言会简单一点。不过普适性后面那题会好一点。(其实也没有什么大区别,套路上基本是一样的)。
首先是经典套路,我们把 \(t\) 接到 \(s\) 后面,中间用分隔符隔开。然后对新字符串做 SA。然后对于每一个 \(s\) 的后缀求出来他和 \(t\) 的最长匹配长度。具体求法就是对于每个后缀,他和其他后缀的 \(\rm LCP\) 是一个单峰函数,峰值在他自己,所以找到它左边和右边最近的 \(t\) 的后缀,求一下二者 \(\rm LCP\) 的最大值即可。然后对于每一个询问我们二分答案 \(mid\) ,判定就是看 \([l,r-mid+1]\) 这个区间内和 \(t\) 的最长匹配长度是否大于等于 \(mid\) 。
总复杂度是 \(\mathcal O(n\log n+n+q\log n)\)
7.LG2178
这道题的套路还是很常见的。
首先两个酒 r-相似就是说两个后缀的 \(\rm LCP\) 大于等于 \(r\) 。我们首先构建出来 \(h\) 数组,我们考虑从大往小处理 \(h\) 数组中的数。对于当前考虑的 \(h\) 数组中的数 \(h_x\) 而言,相当于他的两边每边任选一个数构成的二元组就是 \(h_x\) 相似的。美味度也可以通过维护两边的最大值,最小值,是否有 \(0\) 进行更新。我们发现这个过程可以用并查集来维护,每次相当于合并两段区间。
需要注意的是 r 相似是可以继承 r+1 相似的答案的。
总复杂度是 \(\mathcal O(n\log n)\)
8.LG4094
首先 \([a,b]\) 段是选择子串,\([c,d]\)是整段都要考虑进去。首先我们对整个字符串求出来 \(h\) 数组,那么对于一个后缀我们知道他和别的串的 \(\rm LCP\) 是一个单峰函数,且峰值在它自己,所以对于给定的一个长度,我们可以二分出来的能使 \(\rm LCP\) 取到这个值的在 \(sa\) 数组上最远的左右端点。
对于一个询问我们考虑二分答案, 这样我们通过上面的方式可以知道能使答案达到二分值 \(mid\) 的一段 \(sa\) 数组上的区间 \([l,r]\) ,同时要想达到这个二分值,那么这个公共串的开始位置一定要在 \([a,b-mid+1]\) 之间。这样就变成一个二维偏序问题。直接建立出来主席树就可以做了。
总复杂度是 \(\mathcal O(n\log^2 n)\)
9.LG4248
这道题做法很多,可以说 \(\rm SA,SAM,后缀树\) 都可以做。这里先描述 \(\rm SA\) 的做法。
首先对于两个后缀 \(i,j\) 他们的 \(\rm LCP\) 就是 \(\min\limits_{k=i+1}^j h_k\) 。显然我们是不能枚举后缀的,这样子复杂度就是 \(\mathcal O(n^2)\) 的了。那我们考虑枚举 \(h\) 然后找到满足这个 \(h\) 是最小的区间有多少个。显然对 \(h\) 数组建一个笛卡尔树就可以很轻松地解决了。
总复杂度:\(\mathcal O(n\log n)\)
10.LG3181
这道题和上面那一道几乎一摸一样,把两个串拼起来,然后整体做 SA,只要改一下笛卡尔树上的统计答案方式就可以了。
总复杂度:\(\mathcal O(n\log n)\)
11.CF427D
这道题由于字符串长度太小了(\(n\le 5000\) ),所以可以说基本上什么做法都能过。
法一:这是一个不动脑子的做法,我们先对 \(t\) 数组做 SA。得到 \(t\) 的每一个后缀的长度最小的只出现一次的前缀,我们记录下来这个数。然后把 \(s\) 和 \(t\) 拼起来,再整体做一遍 SA。我们枚举每个 \(t\) 的后缀,因为这个后缀和其他后缀的 \(\rm LCP\) 是单峰的,所以我们再遍历一遍 \(h\) 数组,找到 \(s\) 的所有后缀中和 我们枚举的这个后缀 \(\rm LCP\) 的最大值和次大值。然后如果最大值和次大值相等或者最大值比我们需要的最小长度还要小,那对于这个后缀而言就是无解。否则我们在对次大值分类讨论,如果次大值比我们需要的最小长度小,那我们就取我们需要的最小长度;如果次大值比我们需要的最小长度大,那我们就取次大值+1。当然了,如果没有次大值,且最大值比我们需要的最小长度大,我们也可以取最大值。这个方法复杂度为 \(\mathcal O(n^2)\) 。
法二:上面这个几乎把所有可能都枚举了一遍,实在是太蠢了。我们现在直接对 \(s\) 和 \(t\) 的拼接串做 SA。然后我们由于单峰的影响,我们发现我们只需要考虑相邻的两个 \(sa\) 位置的贡献,即如果 \(sa_i\) 和 \(sa_{i+1}\) 属于不同的字符串,那么这两个串就有可能产生贡献,其他的情况如果产生贡献一定不优。当然还应该满足 \(h_{i+1}>\max{(h_i,h_{i+2})}\) ,这时候令答案和 \(\max(h_i,h_{i+2})+1\) 取 \(\min\) 即可。
这个方法总复杂度为 \(\mathcal O(n\log n)\) 。
12.LG3649
首先我们要知道一个字符串的本质不同回文子串数量是 \(\mathcal O(n)\) 的。然后我们考虑 Manacher 统计回文串的过程,相同的回文串会被过掉,所以跑一遍 Manacher就可以得到所有的本质不同回文串。对与一个回文子串的出现次数的统计是简单的 SA+二分可以做到单词询问 \(\mathcal O(\log n)\) 。把这两个拼一下即可,需要注意不要计算以 Manacher 添加的分隔符为开始的回文串。其他都是细节了。
总复杂度是 \(\mathcal O(n\log n)\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号