Atcoder 题目选做

ABC257 G

直接考虑 \(\rm KMP\) 的过程。\(\rm KMP\) 可以帮助我们求出 \(S\) 的 \(border\) ，并找到 \(T\) 中每一个位置能匹配上的 \(S\) 的最长前缀。

那么我们就可以很轻松的在 \(T\) 的每一个位置找到他能匹配到的 \(S\) 的前缀。由此，我们在 \(T\) 上做 \(DP\) ，令 \(dp_i\) 表示考虑到 \(T\) 的第 \(i\) 个字符，到这个位置需要的 \(S\) 的最小前缀数。

但是直接这样做 \(DP\) ，复杂度最坏还是 \(O(n^2)\) 的，所以我要做一点小优化。考虑我们在给 \(T\) 匹配 \(S\) 前缀的过程，我们如果直接有 \(s_{j+1}=t_i\) ，而没有经过跳 \(\pi\) 的过程，那我们可以直接从 \(i-1\) 转移答案。具体的，当这个时候 \(j=0\) ，那么 \(dp_i=dp_{i-1}+1\) ，否则 \(dp_i=dp_{i-1}\) 。这样子，复杂度最坏是 \(O(n\log n)\) 。

代码：Link

ARC149 D

又是切不动的 700 题。

首先，我们考虑所有在 \([1,10^6]\) 的点经过 \(M\) 次操作后的情况。

其次通过观察可以得知 \(x\) 和 \(-x\) 在经过相同的一系列操作后，只要中间没有到过 \(0\) ，最后结束位置也是对称的。（性质 \(A\) )

那么，每经过一次操作，我们都可以吧当前的整段序列看作 3 个部分：1.正数 2.0 3.负数 。又因为上面的性质 \(A\) ，我们在这之后只用考虑 正数 和 负数 中一个即可，另一部分完全可以推出来。

首先我们肯定会选择正数 和 负数 中数量多的那一部分，为了更好的在最后得到少的那一部分的答案，我们考虑对于少的那一部分的每一个编号连一条边，连到另一部分的它所对应的编号那里去。然后就不再考虑少的那一部分的情况了。

这样做到最后我们就得到了一颗森林（编号组成的），我们遍历每一棵树，如果这棵树的根在中间到达过 \(0\) ，那么这棵树的所有结点的编号都会在那个时间点到达 \(0\) 。如果没有到达过 \(0\) ，那么没经过一条边，最终的位置的下标就会取反一次。

这样子就可以得到所有 \([1,10^6]\) 之内的数的结果了。

具体实现的话，没有必要真的做 \([1,10^6]\) ，找到最大值即可。同时可以维护四个指针 \(l,r,L,R\) ，分别表示当前的编号区间和下标区间，这样子在做每次操作的时候，就好维护剩下的区间和连边了。

复杂度：\(\mathcal O(M+\max{X_i})\)

代码：Link

最后放一张官方题解的解释图。

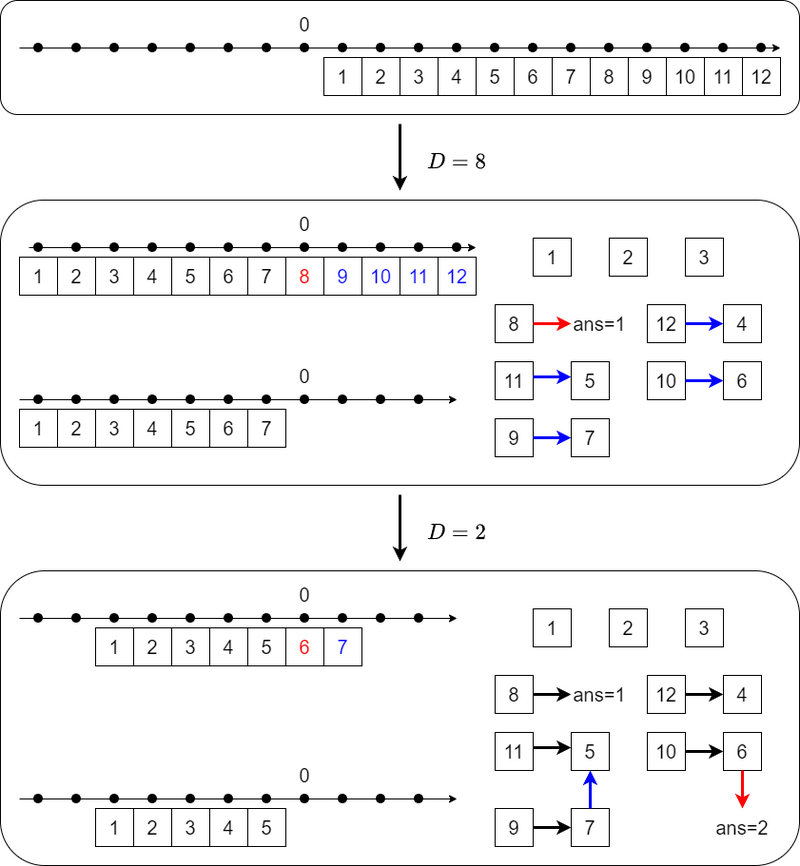
ARC149 E

神仙题/bx

首先题面里又是下标取模，又是重排序，看着很难受。不妨转化一下题面。

给定一个序列 \(A\) 。进行以下操作 \(K\) 次。

• 把 \((A_0,A_1,...A_{M-1})\) 从小到大排序
• 把整个序列 \(A\) 向左循环平移一位。

以样例为例：\((4,1,5,6,2,3)\rightarrow (4,5,6,2,3,1)\rightarrow (5,6,2,3,1,4)\rightarrow(5,6,3,1,4,2)\rightarrow (5,6,1,4,2,3)\rightarrow (5,6,4,2,3,1)\)

相应的 \(B\) 序列也要做一下处理，把 \(B\) 数组整体向左循环平移 \(K\%N\) 次。

然后观察整个过程，可以发现最左边的 \(M-1\) 项在经过至少一次操作后，永远是升序的。那么我们可以把最左边的这 \(M-1\) 项看作左部，右边的 \(N-M+1\) 项看作右部。令左部有 \(L\) 个数，右部有 \(R\) 个数。

我们可以再次简化我们的操作。（左部最后一定是升序的）。

维护左部和右部。每次把右部最前面的数加进左部，左部再把最小的数加到右部的末尾。

进一步观察我们的操作。

可以发现，如果 \(R>K\) ，那么其实只有最开始的前 \(K\) 个右部数会进入左部进行比较，后面的数相对位置不会有任何改变，也不会参与任何比较。我们可以直接扔掉那些没有的数。

如果 \(R<K\) 。那么在进行 \(R\) 次之后，左部一定是 \(\{R+1,R+2,...N\}\) ，右部的数只要进去就一定会被扔出来。从结果上来看左部没有变，右部每次向左循环位移一位。

经过以上分析，我们发现我们总能把问题规约为 \(R=K\) 的情况，然后我们在这个情况下做计数即可。

（此时，\(R=K\) ）。最后结果的左部一定是所有数中最大的 \(L\) 个且按照升序排列，所以如果 \(B\) 序列最左边的数不是所有数中最大的或者不是升序的，那么方案数为 \(0\) 。（所有数并不包含在之前的操作中扔掉的数） 。

设 \(K\) 轮操作之后的右部是 \(\{x_1,x_2,...,x_{R}\}\) ,最初的序列的左部是 \(\{a_1,a_2,...,a_{L}\}\) ，右部是 \(\{b_1,b_2,...,b_{R}\}\) 。

如果右部中存在 \(x_{i-1}>x_{i}\) 的情况，那么最初的序列的右部第 \(i\) 项（\(b_i\)）一定是 \(x_i\) ，因为 \(x_{i-1}\) 是第 \(i-1\) 次操作被左部扔出来的数，而 \(x_i\) 是第 \(i\) 次操作扔出来的数。\(x_i<x_{i-1}\) 说明 \(x_i\) 这个数一定是第 \(i\) 次操作进的左部，刚进去就被扔出来了。

现在忽略掉上面这种 \(x,b\) ，剩下的 \(x\) 一定是升序的。那么对于每一个剩下的 \(x\) ，都有一下要求：

• \(a_1,a_2,...,a_{L},b_1\) 中的一个等于 \(x_1\)
• \(a_1,a_2,...,a_{L},b_1,b_2\) 中的一个等于 \(x_2\)
• \(a_1,a_2,...,a_{L},b_1,b_2,b_3\) 中的一个等于 \(x_3\)
• ......

可以发现对于每一个 \(x\) 都有 \((L+1)\) 中选择方式，所以一共有 \((L+1)^{t}\) 中初始序列（\(t\) 是剩下的 \(x\) 个数）。

又因为原来的左部是无序的，所以答案还应该再乘上 \(L!\) 。

复杂度：\(\mathcal O(N)\)

代码：Link