Codeforces 题目选做
CF1711D
令直接下大雨的点为关键点。
做法一:
首先有结论:对于发大水的点我们只需要考虑关键点即可。
证明:
对于两个相邻的关键点 \(x_i\) 和 \(x_j\) \((x_i<x_j)\) 。令他们的降水量分别为 \(p_i\) 和 \(p_j\) 。考虑中间的一个点 \(pos\) 。
那么考虑这两个关键点对这三个点的影响。
\(a_{x_i}=p_i+p_j-(x_j-x_i)\)
\(a_{pos}=p_i+p_j-(pos-x_i+x_j-pos)=p_i+p_j-(x_j-x_i)\)
\(a_{x_j}=p_i+p_j+(x_j-x_i)\)
因此两个关键点之间的点收到的影响是相同的,且和关键点的影响相同。
我们考虑求出所有关键点的降雨量,这一步可以用两次差分求出。
令 \(c_i=a_i-a_{i-1},d_i=c_i-c_{i-1}\) 。
那么一次降雨 \((x_i,p_i)\) 就可以拆解为:\(d_{x_i-p_i+1}:=d_{x_i-p_i+1}+1\\d_{x_i+1}:=d_{x_i+1}-2\\d_{x_i+p_i+1}:=d_{x_i+p_i+1}+1\) 。
然后做前缀和就可以求出来所有关键点的降水量了。
然后我们只用考虑所有 \(a_{i}>m\) 的关键点即可。对于一次降雨 \((x_j,p_j)\) ,若将其删去满足要求,那么有:\(a_i-(p_j-|x_i-x_j|)\le m\) 。把绝对值式子拆开:
\(\begin{cases}a_i-x_i\le m+p_j-x_j\\a_i+x_i\le m+p_j+x_j\end{cases}\)
对于每一个关键点可以求出 \(\max{(a_i-x_i)}\) 和 \(\max(a_i+x_i)\) 。那么对于任意一次降雨只有满足 \(m+p_j-x_j\ge max(a_i-x_i) \land m+p_j+x_j\ge max(a_i+x_i)\) 。那么才可能没有洪水出现。
复杂度:\(O(n\log n)\)
代码:Link
做法二:
其实前面求 \(a\) 值和做法一的做法是一样的。不过这个做法不是求出所有的关键点的值,而是求出所有极值的 \(a\) 值。(但其实是等价的,因为做法一中已经证明了中间的点一定不会比关键点大)。
我们依次枚举每一次降雨,那么这次降雨被删除后没有洪水,当且仅当所有下雨值都在蓝色的区域内(包括山顶以下的部分)。(图是贺的)/qd
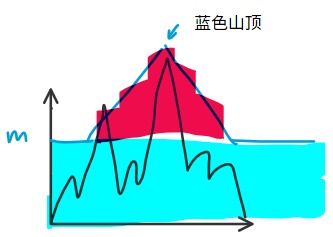
那么我们反过来思考,我们对于所有的极值,我们找到可以包括他的蓝色山顶应位于的区域。然后求所有极值的区域交。
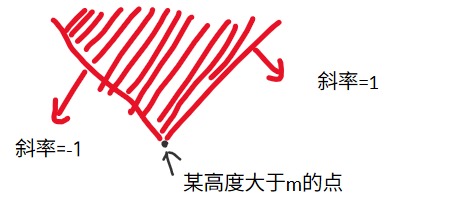
(红色区域就是蓝色山顶关于这个高度大于 \(m\) 的点应位于的区间。)
维护其实是简单的,维护两种斜率的直线就可以了(截距取 \(max\) ),具体见代码/kel。判断一个蓝色山顶的时候也可以直接转换为两条直线。
复杂度:\(O(n\log n)\)
代码:Link
CF1711E
因为有: \(x+y=(x\oplus y)+2(x\land y)\) ,所以可得:\((a\oplus b)+(a\oplus c)=(a\oplus b \oplus a\oplus c)+2((a\oplus b)\land (a\oplus c))=(b\oplus c)+2((a\oplus b)\land (a\oplus c))\) 。
显而易见的,后面的这个式子值是大于等于 \(0\) 的,所以 \((a\oplus b)+(a\oplus c)\) 一定不小于 \((b\oplus c)\) 。所以对于所有的数位只需要一位有 \((a\oplus b)+(a\oplus c)>(b\oplus c)\) 的情况就行了。考虑到这只考虑了 \(a\) 的情况,剩下两个轮换一下就可以了。
做的话直接数位 \(DP\) 。在 \(DP\) 中记录 \(7\) 个量,当前位置,\(a\) 是否达上限,\(b\) 是否达上限,\(c\) 是否达上限,是否已经有 \((a\oplus b)+(a\oplus c)>(b\oplus c)\) ,是否已经有 \((b\oplus a)+(b\oplus c)>(a\oplus c)\) ,是否已经有 \((c\oplus a)+(c\oplus b)>(a\oplus b)\) 。
复杂度: \(O(2^9n)\)
代码:Link
CF762F
主要参考了大象的题解 。
首先观察到数据范围 \(\mid S \mid \leq 1000,\mid T \mid \leq 12\) 。基本上就时状压了。
我们设 \(dp_{i,j}\) 表示 \(S\) 中用 \(i\) 和 \(i\) 的右兄弟匹配 \(T\) 中状态为 \(j\) 的方案数。
具体做的时候,我们直接钦定 \(S\) 的根为 \(1\) ,然后枚举 \(T\) 的根即可。整过过程可以使用记忆化搜索,这样会有很多状态其实根本没有用。
最后答案就是:\(S\) 与 \(T\) 同构的方案数 \(/\) \(T\) 自同构的方案数。
预处理的时候处理出来每个节点的所有儿子和 \(T\) 的儿子集合的状压表示。
复杂度:\(O(\mid T\mid ^2 \times 2^{\mid T\mid}\times \mid S \mid)\)
代码:Link
CF446C
区间加斐波那契是一件困难的事情。
但是斐波那契有通项公式:\(F_n=\dfrac{1}{\sqrt 5}((\dfrac{1+\sqrt 5}{2})^n-(\dfrac{1-\sqrt 5}{2})^n)\) 。而且 \(5\) 在模数 \(1e9+9\) 下也存在二次剩余。(\(\sqrt 5 \equiv 383008016\pmod{1e9+9}\))
那么我们直接把每次区间加斐波那契,改为区间加等比数列,因为公比是固定的,所以懒惰标记记录所有首项就可以了。
注意下传标记时,右儿子的标记要把左儿子的区间跨过去。
复杂度:\(\mathcal O(m\log n)\)
代码:Link
CF1717F
首先考虑让每个数对的两边的点都赋值为 \(-1\) 。那么我们要选择每条边中的一个点 \(+2\) 。那么本题就是询问是否存在这样的一组操作,使得每个点最后的点值为 \(0\) 。(每个点初始点值为 \(a_i\) )。
为了方便我们可以转化一下,令 \(d_i=\frac{a_i-deg_i}{2}\) ,(对于 \(s_i\) 为 \(0\) 的点,令 \(d_i\) 为 \(0\) )。那么每个点初始的时候就是 \(-d_i\) ,现在就是每次选择一个点 \(+1\) ,问最后能否使得 \(d_i\) 都为 \(0\) 。
首先有三种一定不合法的情况:
- \(a_i-deg_i\) 为奇数
- \(d_i<0\)
- \(\sum d_i >m\)
然后我们考虑网络流。
新建源汇点 \(S,T\) 。
对于每一个数对 \((u,v)\) ,新建立一个点。
从 \(S\) 连上下界流量为 \([1,1]\) 的边。从这个点分别连一条上下界流量为 \([0,1]\) 的边到 \(u,v\) 。
对于每一个点。分开考虑 \(s_i=0\) 和 \(s_i\neq 0\) 的点。
对于 \(s_i=0\) 的点,从该点向 \(T\) 连一条上下界流量为 \([0,\infty]\) 的边。
对于 \(s_i=1\) 的点,从该点向 \(T\) 连一条上下架流量为 \([d_i,d_i]\) 得边。
然后直接跑上下界网络流即可。
这里时间复杂度与 \(\infty\) 的取值有着密切的关系。
首先 \(s_i=0\) 的如流量不超过 \(deg_x\) ,所以从该点向 \(T\) 的连边的上界为 \(deg_x\) 即可。由于是有源汇上下界可行流,所以还要新建源汇点 \(T',S'\) ,那么原来源汇之间还要连 \(T\rightarrow S\) 上下界流量为 \([0,\infty]\) 。整个图的流量不会超过 \(m\) ,所以这个 \(\infty\) 取 \(m\) 即可。
复杂度:\(\mathcal O((n+m)n)\)
代码: Link
Gym103428G
和同学 \(\rm ACM\) 被这道题搞破防了。这种套路的题在 \(\rm ABC269\ G\) 中再次出现。
显而易见的,这道题要求对每一个 \(k\ (1\leq k\leq m)\) 求 \(\prod\limits_{i=1}^n\binom{k}{a_i}\) 。
经过一系列的转化和尝试后,我们发现这个式子很难有更好的求解形式。
这时我们注意到 \(\sum{a_i}\leq 10^5\) ,又有 \(a_i\leq 10^5\) 。所以本质不同的 \(a_i\) 最多只有 \(\sqrt n\) 种。
我们考虑每个 \(k\) 的时候,我们只要遍历所有的 \(k\) 求贡献即可。
复杂度: \(\mathcal O(m\sqrt n)\)
代码:Link
Gym103102I
对于任何大于等于 \(2\) 的数 \(x\) 。\(1\ \rm mod\ x,2\ \rm mod \ x, x\ \rm mod\ 1,x\ \rm mod \ 2\) ,都是小于 \(2\) 的。所以 \(1\) 和 \(2\) 的左右填任何数都是可以的。因此我们可以用 \(1\) 和 \(2\) 把数列分成两个部分。
进一步的,可以发现每一个部分中填的数一定是严格递减的。(否则一定存在相邻的 \(x,y\) 满足 \(x<y\) ,那么有 \(x\ \rm mod\ y>2\) 不满足要求)。
现在我们设计一个 \(DP\) ,令 \(dp_x\) 表示我们把 \(n\sim x\) 填到两个部分中且 \(x\) 和 \(x+1\) 不在同一个部分中。
我们从 \(dp_n\) 递推到 \(dp_3\) 。递推到 \(dp_x\) 时,我们找到所有的 \(p\) 满足 \(p\ \rm mod \ x\le 2\) ,这相当于让 \(p-1 \sim x+1\) 都放到一个部分中, \(x\) 接到 \(p\) 的后面, \(dp_x+=dp_{p-1}\) 。
答案首先是$\sum\limits_{i=3}^n dp_i $ 。然后要注意加上所有的数都在一个部分的方案数。
因为排列时循环同构的,所以答案再乘上 \(n\) 。
代码:Link
CF1734F
设这个序列为 \(P\) ,首先这个序列有一个性质,\(P_i=popcount(i)\%2\) 。
做法一:
考虑数位 \(\rm DP\) ,我们要求最后这两个 \(01\) 串不同数位的数量,那么也就是对应数位的下标 \(popcount\) 加起来为奇数的数量,也就是 \(i\) 和 \(i+n\) 。
我们从二进制高维往低位 \(\rm DP\) 。设计 \(\rm DP\) 状态 \(dp_{now,ans,trail,limit}\) 表示当前是第 \(now\) 位,当前两个位置 \(popcount\) 加起来模 \(2\) 的余数,当前 \(i+n\) 的末尾连续 \(1\) 的个数,是否达到了上界。
转移有三种情况: (设 \(d\) 为 \(n\) 的第 \(now\) 位,\(r\) 为我们选择的下一位)
- \(d+r=0\) 。那么 \(dp_{now,ans,trail}\rightarrow dp_{now-1,ans,0}\)
- \(d+r=1\) 。那么 \(dp_{now,ans,trial}\rightarrow dp_{now-1,ans+r+d+r,trail+1}\)
- \(d+r=2\) 。那么 \(dp_{now,ans,trail}\rightarrow dp_{now-1,ans+trail+d+1,0}\)
注:我们要统计 \(i\) 和 \(i+n\) 的 \(popcount\) 的和。
最后当 \(now=-1\) 的时候,如果 \(ans=1\) 且 \(limit=0\) 那么返回 \(1\) ,否则返回 \(0\) 。(\(limit=0\) 是因为下标最大到 \(m-1\) )。
复杂度:\(\mathcal O(t\log^2(max))\)
代码:Link
做法二:(感谢 \(hungry123\) 教会我这个做法)
因为有 \(P_i=popcount(i)\% 2\) 。
所以有以下结论:(\(i,j\) 均为偶数)
- 若 \(P_{i}\neq P_{j}\) ,则有 \(P_{i+1}=P_j\) 。反之亦然
- 若 \(P_{i} = P_{j}\) ,则有 \(P_{i+1}=P_{j+1}\) 。反之亦然
令我们所求为 \(calc(n,m)\) 。首先如果 \(m\) 为奇数,我们可以 \(O(1)\) 的比较 \(P_{m-1}\) 和 \(P_{m-1+n}\) 是否相同,从而把 \(m\) 转化为偶数。
我们对 \(n\) 的奇偶性分类讨论。
如果 \(n\) 为偶数:
如果 \(n\) 为奇数:
递归的边界是 \(n=0\) 或者 \(m=0\) ,这时答案就是 \(0\) 。
复杂度:\(\mathcal O(t\log^2 (max))\)
代码:Link
CF1730D
设两串分别为 \(S,T\) 。\(T'\) 为 \(T\) 的反串。
观察可以得到结论:把 \(T'\) 和 \(S\) 的相同位两个数看作一个无序二元组。那么无论怎样操作,无序二元组不会变化。
那么如果最后 \(S\) 和 \(T\) 能变为两个相同的字符串,那么所有无序二元组一定构成“回文串” 。只需要检查所有无序二元组是否可以全部匹配上就可以了。(串长为奇数的话,会有一个无序二元组多出来,且这个二元组两个元素相同)。
证明先略。
复杂度:\(\mathcal O(n^2)\)
代码: Link



 浙公网安备 33010602011771号
浙公网安备 33010602011771号