傅里叶级数
傅里叶在他的专著《热的解析理论》中提出,任何一个周期函数都可以表示为若干个正弦函数的和,即:
\[f(t)=a_0+\sum_{n=1}^{\infty}(a_ncos(n\omega t)+b_nsin(n\omega t))$$其中$\omega=\dfrac{2\pi}{T}$,$T$为函数的周期。$a_n/b_n$和$n$分别控制了正弦波的振幅与频率。这就是傅里叶级数的**三角形式**。
我们还可以用**复指数形式[^1]**和**积分[^2]**来表示傅里叶级数:
$$ f(t)=\sum_{n=-\infty}^{\infty}F_ne^{in\omega t} $$ $$ F_n=\frac{1}{T}\int_0^T f(t)e^{-in\omega t} dt $$其中$F$就是周期函数$f$的**傅里叶级数(Fourier Series, FS)**。
**如果说$f$是某段信号在时域上的表现,$F$就是其在频域上的表现。傅里叶变换实现的就是从时域到频域的变换。**
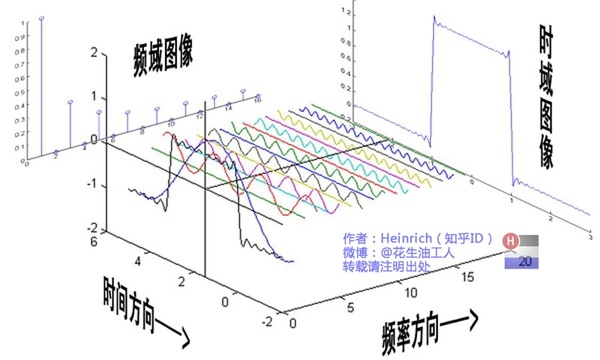
##傅里叶变换
对于非周期函数,我们可以将其视为一个以$(-\infty,\infty)$为一个周期的周期函数。
经过数学推导,得到:
$$ F(\omega)=\int_{-\infty}^\infty f(t)e^{-i\omega t} dt$$ $$ f(t)=\frac{1}{2\pi}\int_{-\infty}^\infty F(\omega)e^{i\omega t} d\omega $$ 这叫做**傅里叶变换(Fouier Transform, FT)**及**傅里叶逆变换(IFT)**。
注意,其结果都可能是复数。
这时,$F$不再是离散的级数,而是一个连续的函数了。
与傅里叶级数的比较:
- 傅里叶级数:周期信号,离散频率,频率分量的值
- 傅里叶变换:非周期信号,连续频率,频率分量的**密度**
##卷积定理
卷积定理有两个:
$$ FT[f_1(t)*f_2(t)]=FT[f_1(t)]\cdot FT[f_2(t)] $$ $$ IFT[F_1(\omega)*F_2(\omega)]=\frac{1}{2\pi}IFT[F_1(\omega)]\cdot IFT[F_2(\omega)] $$ 分别称为**时域卷积定理**和**频域卷积定理**。
> 下面对时域卷积定理进行证明。
\]
\begin{align}
FT[f_1(t)f_2(t)] &= FT[\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau) d\tau] \
&= \int_{-\infty}\infty[\int_{-\infty}\infty f_1(\tau)f_2(t-\tau) d\tau]e^{-i\omega t} dt \
&= \int_{-\infty}^\infty f_1(\tau)[\int_{-\infty}^\infty f_2(t-\tau)e^{-i\omega t} dt]d\tau \
&= \int_{-\infty}^\infty f_1(\tau)[\int_{-\infty}^\infty f_2(t)e^{-i\omega (t+\tau)} dt]d\tau \
&= \int_{-\infty}^\infty f_1(\tau)e{-i\omega\tau}[\int_{-\infty}\infty f_2(t)e^{-i\omega t} dt]d\tau \
&= \int_{-\infty}^\infty f_1(\tau)e^{-i\omega\tau}F_2(\omega) d\tau \
&= F_2(\omega) \int_{-\infty}^\infty f_1(\tau)e^{-i\omega\tau} d\tau \
&= F_1(\omega)F_2(\omega)
\end{align*}
\[ 其实基本上就是直接展开啦。频域卷积定理的证明也是类似的。
可以观察到,在一个域上进行卷积,相当于在另一个域上进行点积。这启发我们用复杂度低的点积运算来代替复杂度高的卷积运算。
##离散时间傅里叶变换
以上的内容都是针对连续信息/连续函数的。但是,计算机是无法存储连续的信息的,只能每隔时间$T$对信息进行采样。也就是说,计算机把**连续的函数**转化为了**离散的序列**。对于这样一个序列进行的傅里叶变换就称为**离散时间傅里叶变换(Discrete Time Fouier Transform, DTFT)**。
$$ F(\omega)=\sum_{n=-\infty}^\infty f(nT)e^{-i\omega nT } $$ 我们其实是用离散的采样点$nT$代替了FT中连续的时间$t$。进一步,由于采样的结果本质上是一个序列,那么我们可以把序列中连续两项的间隔,也就是采样频率$T$看做**单位“1”**。我们用$x(n)$表示采样结果序列,那么有:
$$ X(\omega)=\sum_{n=-\infty}^\infty x(n)e^{-i\omega n} $$ 事实上,这个将$T$转化为“1”的过程,就是模拟信号转化为数字信号的过程。
其逆变换IDTFT的表达式为:
$$ x(n)=\int_{-\pi}^\pi X(\omega)e^{i\omega n} d\omega\]
离散傅里叶变换
通过DTFT,我们已经能够处理离散的采样信号了。但由于采样结果序列依然是无限长的,计算机还是无法进行处理。从DTFT的式子中可以看出,\(X(\omega)\)是以\(2\pi\)为周期的,那么解决的方法很简单:我们只从时域\((0,2\pi)\)上均匀地取\(N\)个点,用这\(N\)个点计算出频域上的\(N\)个点,这\(N\)个点就可以作为频域上的一个周期。
\[ X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad (k=0,1,2...,N-1)$$ 其中$W_N=e^{-i\frac{2\pi}{N}}$,也就是n次单位根。
其实DFT就是将DTFT中的对$\omega$积分替换为对$\frac{2k\pi}{N}$求和[^3]。
这样,我们就得到了一个$N$点信号到$N$点频域的离散变换,这个变换就叫做**离散傅里叶变换(Discrete Fourier Transform, DFT)**。
其逆变换的表达式为:
$$ x(n)=\frac{1}{N} \sum_{k=0}^{N-1}X(k)W_N^{-nk} \quad (n=0,1,2...,N-1)\]
FS, FT, DTFT, DFT的比较
| 变换 |
特点 |
| 傅里叶级数FS |
周期信号,离散频率,频率分量的值 |
| 傅里叶变换FT |
非周期信号,连续频率,频率分量的密度 |
| 离散时间傅里叶变换DTFT |
非周期采样信号,连续频率,频率分量的密度 |
| 离散傅里叶变换DFT |
有限长度非周期采样信号,离散频率,对于DTFT频谱频率分量的密度 |
快速傅里叶变换
朴素进行DFT的复杂度是\(O(n^2)\),这可以从其表达式中看出。事实上我们有一种利用分治进行DFT的\(O(nlogn)\)算法,这就是常常被应用在OI中的快速傅里叶变换(Fast Fourier Transform, FFT)。
为了方便,以下若不做特殊说明,\(N\)均是\(2\)的整数次幂,这可以通过在原来的序列后补若干个\(0\)至有\(2\)的整数次幂项来实现。
\[\begin{align}
X(k) &= \sum_{n=0}^{N-1}x(n)W_N^{nk} \\
&= \sum_{n=0,n+=2}^{N-2}x(n)W_N^{nk} + \sum_{n=1,n+=2}^{N-1}x(n)W_N^{nk} \\
&= \sum_{n=0}^{\frac{N}{2}-1}x(2n)W_N^{2nk} + \sum_{n=0}^{\frac{N}{2}-1}x(2n+1)W_N^{(2n+1)k} \\
&= \sum_{n=0}^{\frac{N}{2}-1}x(2n)W_{\frac{N}{2}}^{nk} + W_N\sum_{n=0}^{\frac{N}{2}-1}x(2n+1)W_{\frac{N}{2}}^{nk}
\end{align}
$$ 通过以上变形,原问题变成了两个规模减半的子问题。合并两个子问题的复杂度是$O(1)$,分治层数为$O(logn)$,所以计算一项的复杂度是$O(logn)$,计算$n$项的复杂度是$O(nlogn)$。
##例题:多项式乘法
设$n$次多项式$f_1(x)=\sum_{i=0}^{n}a_ix^i$和$m$次多项式$f_2(x)=\sum_{i=0}^{m}b_ix^i$的积为$n+m$次多项式$f_3(x)=\sum_{i=0}^{n+m}c_ix^i$。给出序列$a,b$,求序列$c$。
容易知道$c_k=\sum_{i=0}^{k}a_ib_{k-i}$,事实上序列$c$就是序列$a$和序列$b$的**离散卷积**。
那么根据卷积定理,$c_k=IDFT[DFT[c_k]]=IDFT[DFT[a_k*b_k]]=IDFT[DFT[a_k]\cdot DFT[b_k]]$
所以我们只要将序列$a$和$b$DTFT到频域,点积后再IDTFT回时域,就可以得到序列$c$啦。
> 时间复杂度$O((n+m)log(n+m))$。
##快速数论变换
在我们进行DTFT的过程中,使用的是复数。如果精度要求很高(比如求方案数),用复数来进行FFT就会出现误差。所以我们需要找到一个与复数单位根有相似性质的替代。
注意到FFT能够进行的根本因素就是复数单位根具有$W_N^2=W_{\frac{N}{2}}$这一性质。事实上,模意义域下的原根[^4]就是复数单位根的一个很好的替代。
定义$W_N=g^{\frac{P-1}{N}}(mod \ P)$,则有:
$$ X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad (mod \ P)$$ 这就是**快速数论变换(Number Theory Transform, NTT)**。
进行NTT时,最常用的模数就是998244353,其原根$g=3$。
##Code
[UOJ34 - 多项式乘法](http://www.cnblogs.com/VisJiao/p/uoj34.html)
[^1]:$e^{i\theta}=cos\theta+isin\theta$
[^2]:$\int_a^b f(x)dx$表示对$x\in(a,b)$的$f(x)$进行积分。
[^3]: 把这个式子转化成类似DTFT的形式:
$$ X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk}=\sum_{n=0}^{N-1} x(n)e^{-i \frac{2k\pi}{N}n} $$ $\frac{2k\pi}{N}$代替的就是DTFT中$\omega$的位置。
[^4]: $P$的原根$g$定义为使得$g^0,g^1,...,g^{P-2} \ (mod \ P)$互不相同的数。\]

