解数独(leetcode37)

编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 '.' 表示。

 

 

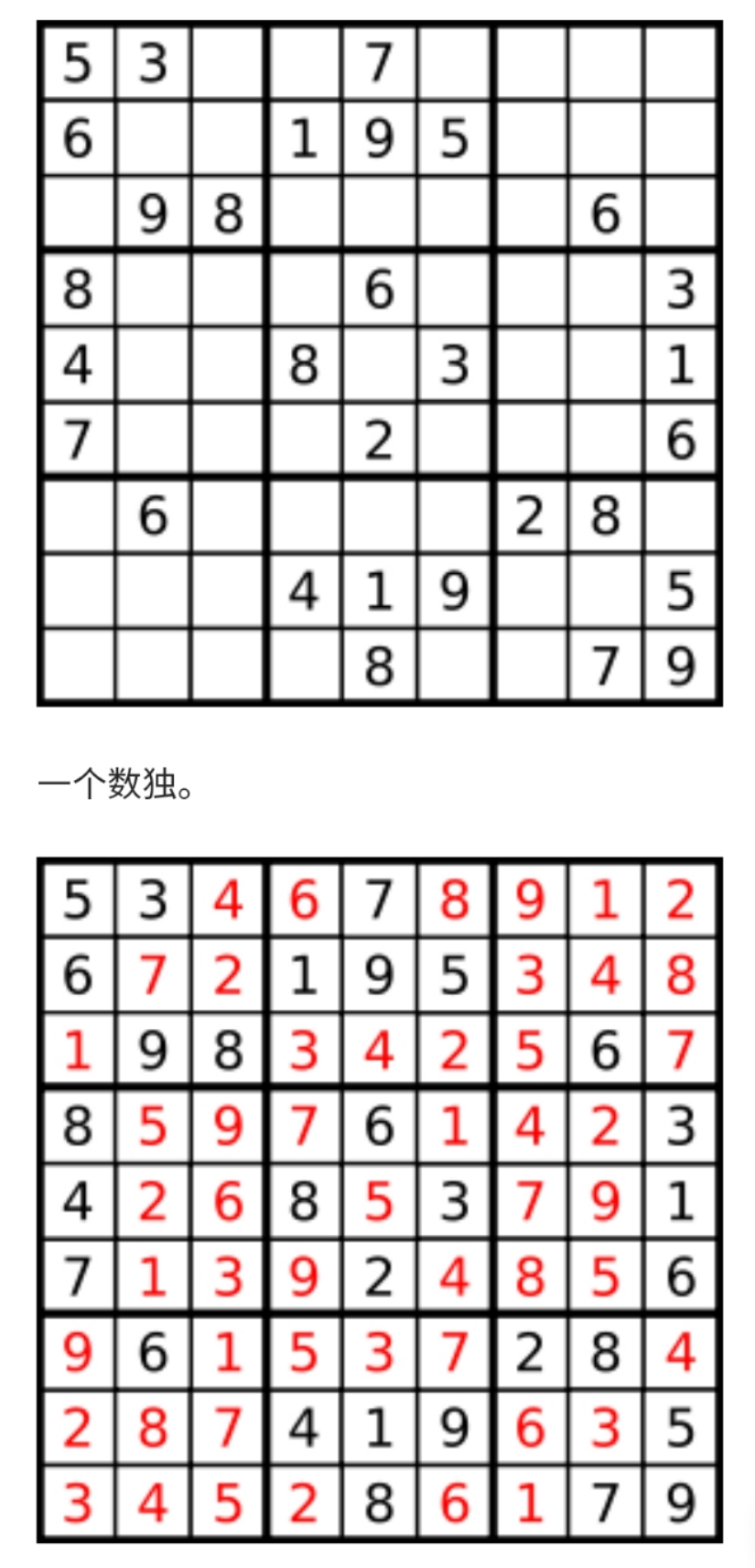
解析：

可以考虑使用行优先的顺序依次枚举每一个空白格中填的数字，通过递归+回溯枚举所有可能的填法。

当递归到最后一个空白格后，还没有冲突，说明我们找到了答案；而如果当前空白格不能填下任何一个数字，就进行回溯。

　　由于每个数字在同一行，同一列，同一个九宫格只能出现一次，我们可以使用 line[ i ], column[ j ] , block[x][y]分别表示第i行，

第j列，和第（x,y）个九宫格中填下数字的情况。

方法一：

递归+回溯

我们用数组记录每个数字是否出现。

因为我们填写的数字范围是【1，9】，而数组的下标从0开始，

因此在存储时，我们使用一个长度为9的布尔类型的数组。如果数字 i+1 出现过，则令 第 i 个元素的值为 true 。

例如，line[2][3] = true，表示数字4在第2行已经出现过。则遍历第2行空白格时，不能再填4.

　　首先，遍历数独数组，标记空白格位置和已出现数字所在的行，列，九宫格信息。

然后开始递归枚举，判断位置为i和j位置的单元格，能否填入1-9，如果可以，继续递归判断下个空白格位置。否则，回溯。

public class Leetcode37 {
    private boolean[][] line = new boolean[9][9];
    private boolean[][] column = new boolean[9][9];
    private boolean[][][] block = new boolean[3][3][9];

    private boolean valid = false;
    private List<int[]> spaces = new ArrayList<int[]>();

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        char[][] board = new char[9][9];
        board[0]=new char[]{'5','3','.','.','7','.','.','.','.'};
        board[1]=new char[]{'6','.','.','1','9','5','.','.','.'};
        board[2]=new char[]{'.','9','8','.','.','.','.','6','.'};
        board[3]=new char[]{'8','.','.','.','6','.','.','.','3'};
        board[4]=new char[]{'4','.','.','8','.','3','.','.','1'};
        board[5]=new char[]{'7','.','.','.','2','.','.','.','6'};
        board[6]=new char[]{'.','6','.','.','.','.','2','8','.'};
        board[7]=new char[]{'.','.','.','4','1','9','.','.','5'};
        board[8]=new char[]{'.','.','.','.','8','.','.','7','9'};
        
        Leetcode37 leet = new Leetcode37();
        leet.solveSudoku(board);
        for(int i=0;i<9;i++){
            for(int j=0;j<9;j++){
                System.out.print(board[i][j]+" ");
            }
            System.out.println();
        }
    }

    public void solveSudoku(char[][] board) {

        //遍历数独，标记空白格位置，及数字所在行，列，及九宫格
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] == '.') {// 存储空白格的位置
                    spaces.add(new int[] { i, j });
                } else {
                    // 当数字i+1出现过时，令第i个元素的值为true，所以，这里表示第digit位置的值为true
                    int digit = board[i][j] - '0' - 1;
                    // 表示digit+1在第i行出现过，并且在第j列出现过，并且在位置为i/3,j/3的九宫格出现过
                    line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
                }
            }
        }

        dfs(board, 0);
    }

    //递归+回溯
    public void dfs(char[][] board, int pos) {
        if (pos == spaces.size()) {// 如果位置等于空白格的大小，则valid为true
            valid = true;
            return;
        }
        int[] space = spaces.get(pos);
        int i = space[0], j = space[1];

        //遍历0-8的位置，实际是为了判断1-9这几个数字在对应位置是否已经出现过
        for(int digit=0;digit<9&&!valid;++digit){
            //在第i行，第j列，第i/3,j/3个九宫格中，digit都还没出现
            if(!line[i][digit]&&!column[j][digit]&&!block[i/3][j/3][digit]){
                line[i][digit]=column[j][digit]=block[i/3][j/3][digit]=true;
                board[i][j] = (char)(digit+'0'+1);
                dfs(board,pos+1);
                line[i][digit]=column[j][digit]=block[i/3][j/3][digit]=false;
            }
        }
    }

}