链表

 

1.数组和链表的内存分布

数组需要一块连续的内存空间，而链表则通过“指针”将一组零散的内存块串联起来

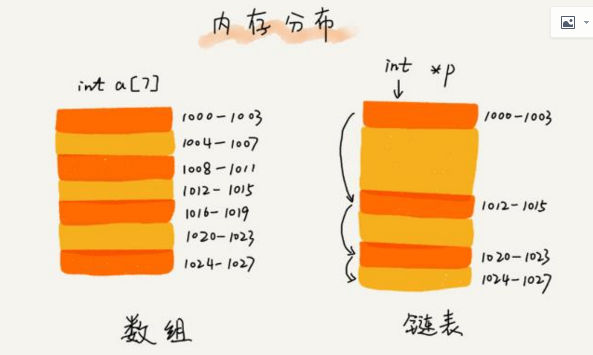
2.三种常见的链表

单链表、双向链表、循环链表

2.1 单链表

链表通过指针将一组零散的内存块串联在一起。其中内存块称为结点，并且还有一个记录下个结点地址的指针，叫做后继指针next。

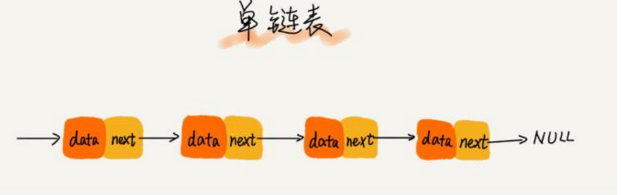
其中，第一个结点叫首节点，最后一个结点叫做尾结点。头结点用来记录链表的基地址，有了它，我们才可以便利得到整条链表。而尾结点特殊的地方是：指针不是指向下一个结点，而是指向一个空地址null,表示链表上最后一个结点。

数组的插入和删除时间复杂度是O(n),而链表的插入和删除的时间复杂度是O(1)，所以链表的插入和删除是非常快速的。

如下图（链表的插入和删除）

但是相对的，如果链表想要随机访问第k个元素，就没有数组高效了。此时链表的时间复杂度为O(n),而数组的时间复杂度为O(1)。

2.2 循环链表

循环链表是一种特殊的单链表，它的尾结点的指针指向链表的头结点。

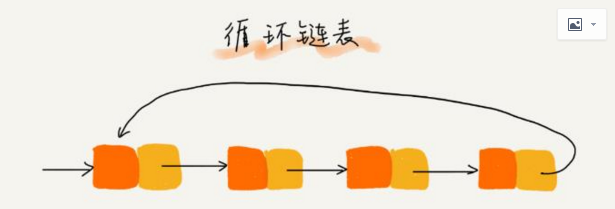
相对于单链表，循环链表的优点是：从链尾到链头比较方便。

当要处理的数据具有环型结构特定时，就比较适合采用循环链表。比如约瑟夫问题

2.3 双向链表

单链表只有一个后继指针 next 指向后面的结点。而双向链表，它支持两个方向，每个结点不止有一个后继指针 next 指向后面的结点，还有个前驱指针 prev 指向前面的结点。

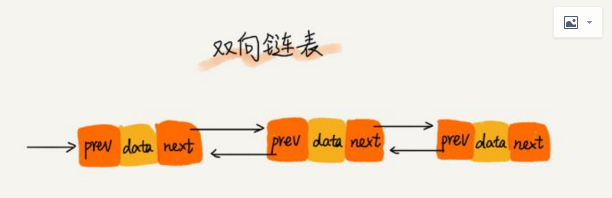
从上图可以看出，双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以存储同样多的数据，双向链表要比单链表占用更多的内存空间。但是因为双向链表支持双向遍历，所以双向链表相对单链表更灵活。

 

前面我们说到单链表的插入、删除操作的时间复杂度已经是O(1)了，那么双向链表还能怎样高效呢？

 

实际上，这种说法是不太准确的，它是由先决条件的。

这里以删除操作为例。

在实际软件开发中，从链表中删除一个数据无非两种情况：

• 删除结点中“值等于某个给定值”的结点
• 删除给定指针指向的结点

① 对于第一种情况，不管是单链表还是双链表，为了查找值等于给定值的结点，都需要从头结点一个一个依次遍历对比，直到找到值等于给定值的结点，然后再通过指针操作将其删除。

 

尽管单纯的删除操作时间复杂度是O(1),但是遍历查找的时间是主要的耗时点，对应的时间复杂度为O(n)。根据时间复杂度分析中的加法法则，删除值等于给定值的结点对应的链表操作的总时间复杂度为O(n)。

 

② 对于第二种情况，我们已经知道了要删除的结点，所以要删除某个结点q 需要知道其前驱结点，而单链表不支持直接获取前驱结点，所以需要从头结点开始遍历链表，直到 p->next=q,说明p是q的前驱结点。

但是对于双链表，因为链表的结点中已经保存了前驱结点的指针，所以不需要遍历。

所以，针对第二种情况，单链表的时间复杂度为O(n),而双链表为O(1)。

 

插入操作与上面删除类似。

另外双向链表的按值查询的效率也要比单链表高一些。因为我们可以记录上次查找的位置p,每次查询的值与p的大小关系，决定是往前还是往后查找，所以平均只需要查找一半的数据。？？？（感觉这里应该有个前提：有序）

 

LinkedHashMap的实现原理？？

 

空间换时间的设计思想

当内存空间充足的时候，并且我们更追求代码的执行速度，我们可以选择空间复杂度相对较高，但是时间复杂度相对很低的算法或数据结构。相反，如果内存比较紧缺，例如代码跑在手机或者单片机上时，我们可以反过来用时间换空间的设计思路

 

其中缓存就是典型的空间换时间。

 

这里总结下：对于执行较慢的程序，可以通过消耗更多的内存（空间换时间）来进行优化；而消耗过多的内存的程序，可以通过消耗更多的时间（时间换空间）来降低内存的消耗。

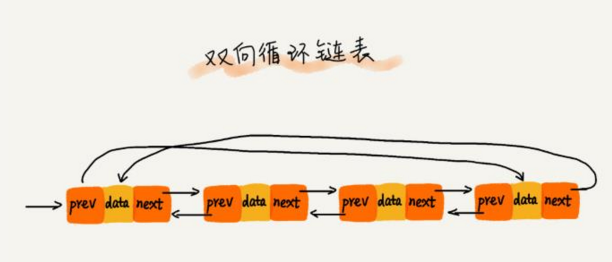
2.4 双向循环链表

每个结点存储有前驱指针，后继指针。并且尾结点的后继指向头节点，头结点的前驱指向尾结点。

3. 链表VS数组性能对比

3.1 链表和数组时间复杂度对比

3.2 实际开发中，不能仅仅利用时间复杂度分析就决定选择哪个数据结构来存储数据，下面是一些链表和数组使用的情况。

(1). 因为数组在实现上使用的是连续的内存空间，可以借助cpu的缓存，预读数组中的数据，所以访问效率更高。而链表因为在内存中不是连续存储的，所以对cpu缓存不友好，不能预读。

(2). 数组因为大小固定，且占用连续的内存空间，所以如果数组声明过大，系统没有足够的连续的内存空间分配给他，则会导致“内存不足”。而如果数组声明过小，在数组不够用时，则需要重新申请一个更大的内存空间，并且把原数组复制过去。这很费时。而链表本身没有大小限制，天然支持扩容。

注：对于java中的ArrayList容器，虽然也支持动态扩容，但是如果数组没有空闲空间时，会申请一个更大的内存空间，并且把数据复制过去。而数据复制的操作是很耗时的。

(3). 如果你对代码的内存使用很苛刻，那么最好用数组。因为链表中的每个节点都需要消耗额外的存储空间去存储指向下一个结点的指针，这会使内存消耗加倍。另外，对链表进行频繁的插入，删除操作，会导致频繁的内存申请和释放，这容易造成内存碎片，而如果是java语言，则可能会导致频繁的GC（Garbage Collection , 垃圾回收）。

4.如何基于链表实现LRU缓存淘汰算法

缓存是一种提高数据读取性能的技术，常见的有CPU缓存、数据库缓存、浏览器缓存等。

缓存大小有限，当缓存满时，就需要确定哪些数据应该被清理，哪些数据应该被保存？

这就需要缓存淘汰策略来决定。

常见的缓存淘汰策略：先进先出策略FIFO（First In , First Out）、最少使用策略LFU（Least Frequently Used）、最近最少使用策略LRU（Least Recently Used）

 

那么， 如何基于链表实现LRU缓存淘汰算法呢

思路：维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的（即最近访问的会靠近链表头）。当有一个新的数据被访问时，我们从链表头部开始顺序遍历链表。

1.如果此数据之前已经被缓存在链表中了，我们遍历得到这个数据的结点，并将其从原来的位置删除，然后再插入到链表的头部。

2.如果此数据没有在缓存链表中，又分为两种情况：

• 如果此时缓存未满，则将此结点直接插入到链表的头部；
• 如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。

那么它的时间复杂度是多少呢？因为不管缓存有没有满，我们都需要遍历一遍链表，所以这种基于链表的实现思路，缓存访问的时间复杂度为O(n)。

但是，可以继续优化，比如引入散列表（Hash table）来记录每个数据的位置，将缓存访问的时间复杂度降到O(1)。

 

课后思考。

另外除了基于链表的实现思路，如何用数组实现呢？

课后思考：

如何判断一个字符串是否是回文字符串的问题。但是字符串是通过单链表来存储的，那该怎么判断是一个回文串呢？相应的时间复杂度是多少？