快速排序算法(优化)

之前有记录一版快速排序算法。

这里记录对它优化的一个版本。

之前快速排序一个缺点，就是使用递归算法对规模非常大的数据项进行排序可能会引起栈溢出，导致存储错误。

而且上面的代码的实现方式中，对枢纽的不同的选择，会造成不一样的算法的执行效率。

理想情况下，应该选择被排序的数据项的中值数据项作为枢纽。即对快速排序算法来说 拥有两个大小相等的子数组是最优的情况。

而最坏的情况是一个子数组只有一个数据项，另一个子数组含有 N-1 个数据项。这种时候以O（N^2）的效率运行。而且除了慢还有另一个问题，就调用次数的增加，递归工作栈可能会溢出，使系统瘫痪。

总结下就是，在快速排序中，选择最右端的数据项作为枢纽，如果数据项排序任意，那么效率不会太坏。但是，如果数据是有序或者逆序时，从数组的一端或者另一端选择数据项作为枢纽都不是好办法。

 

而更好的枢纽选择方案就很有必要了。

"三数据项取中"划分

折衷的方式是找到数组里第一个、最后一个以及中间位置数据项的居中数据项值，并且设此数据项为枢纽。选择第一个、最后一个以及中间位置数据项的中指被称为"三数据项取中"(median-of-three)方法。

 

 

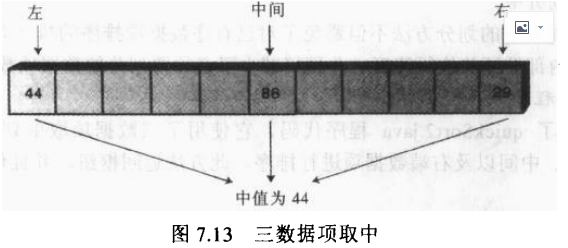
三数据项取中的划分方法不但避免了对已有数据项排序的执行效率为O(N^2), 而且它也提高了划分算法内部循环的执行速度，并且稍稍减少了必须要划分的数据项数目。

算法思想简图同之前快速排序

 不同处在于枢纽选择做了优化

代码如下

package com.vincent.suanfa;

public class quickSort1 {

    public static void main(String[] args){
        int maxSize = 16;
        ArrayIns arr;
        arr = new ArrayIns(maxSize);
        //填充数组
        for(int j=0; j < maxSize; j++){
            long n = (int)(java.lang.Math.random()*99); //生成随机数
            arr.insert(n);
        }
        arr.display();
        arr.quickSort();
        arr.display();
    }
}

class ArrayIns{
    private long[] theArray; //数组
    private int nElems; //标识数组最大下标(即长度-1)
    
    //构造函数
    public ArrayIns(int max){
        theArray = new long[max];
        nElems = 0;
    }
    
    //把数据插入数组
    public void insert(long value){
        theArray[nElems] = value;
        nElems++;
    }
    
    //打印数组
    public void display(){
        System.out.print("A=");
        for(int j=0; j<nElems; j++){
            System.out.print(theArray[j] + " ");
        }
        System.out.println("");
    }
    
    public void quickSort(){
        recQuickSort(0,nElems-1);
    }
    
    public void recQuickSort(int left, int right){
        
        int size = right - left +1;
        if(size<=3){
            manualSort(left,right);
        }else{
            long median = medianOf3(left,right);
            int partition = partitionIt(left, right, median);
            recQuickSort(left, partition-1);
            recQuickSort(partition+1, right);
        }
    }
    
    public long medianOf3(int left,int right){
        int center = (left+right)/2;
        
        if(theArray[left] > theArray[center])
            swap(left,center);
        if(theArray[left] > theArray[right])
            swap(left,right);
        if(theArray[center]>theArray[right])
            swap(center,right);
        
        swap(center,right-1);  //put pivot on right 把枢纽放到右边
        return theArray[right-1];  //返回中间值
    }
    
    
    
    //分区函数
    public int partitionIt(int left, int right, long pivot)
    {
        int leftPtr = left-1;
        int rightPtr = right;
        while(true)
        {
            //leftPtr表示数组下标为leftPtr时，其值小于pivot；目的是找到下标大于等于pivot的下标;即分出pivot左边的部分
            while( theArray[++leftPtr] < pivot);  
            
            //rightPtr表示数组下标为rightPtr时，其值大于pivot;目的是找到下标小于等于pivot的下标;即分出pivot右边的部分
            while(theArray[--rightPtr] > pivot);  
            
            if(leftPtr >= rightPtr)        //表示小于pivot的下标和大于pivot的下标交叉了，分区结束
                break;                    
            else
                swap(leftPtr, rightPtr);  //把数据项按枢纽分成两组
        }
        swap(leftPtr, right);
        System.out.println("分区：");
        display();
        System.out.println("分区下标: "+leftPtr);
        return leftPtr;
    }
    //交换数据
    public void swap(int dex1, int dex2)
    {
        long temp = theArray[dex1];
        theArray[dex1] = theArray[dex2];
        theArray[dex2] = temp;
    }
    
    public void manualSort(int left,int right){
        int size = right - left + 1;
        if(size<=1)
            return;
        if(size == 2)
        {
            if(theArray[left]>theArray[right])
                swap(left,right);
            return;
        }else{
            if(theArray[left] > theArray[right-1])
                swap(left,right-1);
            if(theArray[left] > theArray[right])
                swap(left,right);
            if(theArray[right-1]>theArray[right])
                swap(right-1,right);
        }
    }
}

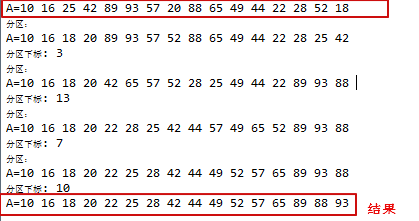
效果如下：