快速排序算法
快速排序算法本质上是通过把一个数组划分为两个子数组,然后递归的调用自身为每一个子数组进行快速排序来实现的。
这里首先讲递归的快速排序算法。
1.递归的排序算法
public void recQuickSort(int left, int right){ if(right-left<=0){ //如果right-left<=0,表示已经排好序了 return; }else{ long pivot = theArray[right]; int partition = partitionIt(left, right, pivot); recQuickSort(left, partition-1); recQuickSort(partition+1, right); } }
正如上面的代码,有三个基本步骤:
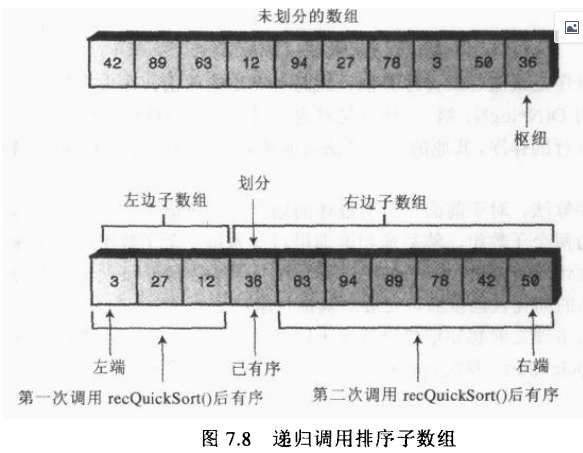
- 把数组或子数组划分成左边(较小的关键字)的一组和右边(较大的关键字)的一组。
- 调用自身对左边的一组进行排序。
- 再次调用自身对右边的一组进行排序。
这个递归的基值(终止)条件:检查数组是否只包含一个数据项,如果是,就定义数组已经有序,方法返回。
那么如何检查数组只包含一个数据项呢?即right - left <= 0;
patitionIt()方法应该使用什么样的枢纽呢?
- 应该选择具体的一个数据项的关键字的值作为枢纽;称这个数据项为pivot(枢纽).
- 可以选择任意一个数据项作为枢纽。为了简便我们总选择待划分的子数组最右端的数据项作为枢纽。
- 划分完成之后,如果枢纽被插入到左右子数组之间的分界处,那么枢纽就落在排序之后的最终位置上了。
递归排序算法思想简图

递归排序实际数据效果图

这里贴出递归方式快速排序代码实现
package com.vincent.suanfa; public class quickSort1 { public static void main(String[] args){ int maxSize = 16; ArrayIns arr; arr = new ArrayIns(maxSize); //填充数组 for(int j=0; j < maxSize; j++){ long n = (int)(java.lang.Math.random()*99); //生成随机数 arr.insert(n); } arr.display(); arr.quickSort(); arr.display(); } } class ArrayIns{ private long[] theArray; //数组 private int nElems; //标识数组最大下标(即长度-1) //构造函数 public ArrayIns(int max){ theArray = new long[max]; nElems = 0; } //把数据插入数组 public void insert(long value){ theArray[nElems] = value; nElems++; } //打印数组 public void display(){ System.out.print("A="); for(int j=0; j<nElems; j++){ System.out.print(theArray[j] + " "); } System.out.println(""); } public void quickSort(){ recQuickSort(0,nElems-1); } public void recQuickSort(int left, int right){ if(right-left<=0){ //如果right-left<=0,表示已经排好序了 return; }else{ long pivot = theArray[right]; int partition = partitionIt(left, right, pivot); recQuickSort(left, partition-1); recQuickSort(partition+1, right); } } //分区函数 public int partitionIt(int left, int right, long pivot) { int leftPtr = left-1; int rightPtr = right; while(true) { //leftPtr表示数组下标为leftPtr时,其值小于pivot;目的是找到下标大于等于pivot的下标;即分出pivot左边的部分 while( theArray[++leftPtr] < pivot); //rightPtr表示数组下标为rightPtr时,其值大于pivot;目的是找到下标小于等于pivot的下标;即分出pivot右边的部分 while( rightPtr>0 && theArray[--rightPtr] > pivot); if(leftPtr >= rightPtr) //表示小于pivot的下标和大于pivot的下标交叉了,分区结束 break; else swap(leftPtr, rightPtr); //把数据项按枢纽分成两组 } swap(leftPtr, right); System.out.println("分区:"); display(); System.out.println("分区下标: "+leftPtr); return leftPtr; } //交换数据 public void swap(int dex1, int dex2) { long temp = theArray[dex1]; theArray[dex1] = theArray[dex2]; theArray[dex2] = temp; } }






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 25岁的心里话
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
2019-05-01 asp.net core 系列之允许跨域访问(Enable Cross-Origin Requests:CORS)