OpenCv 028---图像积分图算法

1 前备知识

    积分图像是Crow在1984年首次提出，是为了在多尺度透视投影中提高渲染速度，是一种快速计算图像区域和与平方和的算法。其核心思想是对每个图像建立自己的积分图查找表，在图像积分处理计算阶段根据预先建立的积分图查找表，直接查找从而实现对均值卷积线性时间计算，做到了卷积执行的时间与半径窗口大小的无关联。图像积分图在图像特征提取HAAR/SURF、二值图像分析、图像相似相关性NCC计算、图像卷积快速计算等方面均有应用，是图像处理中的经典算法之一。 图像积分图建立与查找 在积分图像(Integral Image - ii)上任意位置(x, y)处的ii(x, y)表示该点左上角所有像素之和， 其中(x,y)是图像像素点坐标。

机器视觉中的图像积分图及其实现

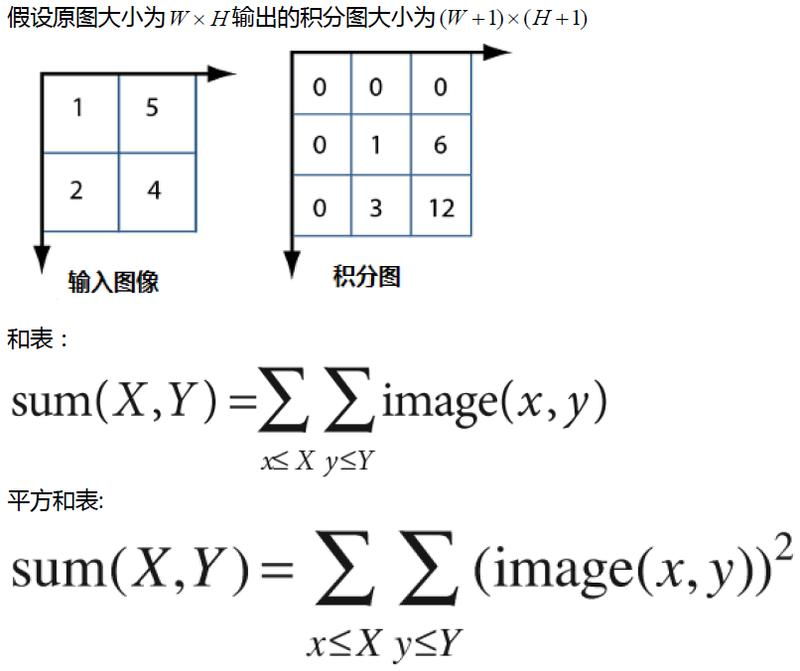
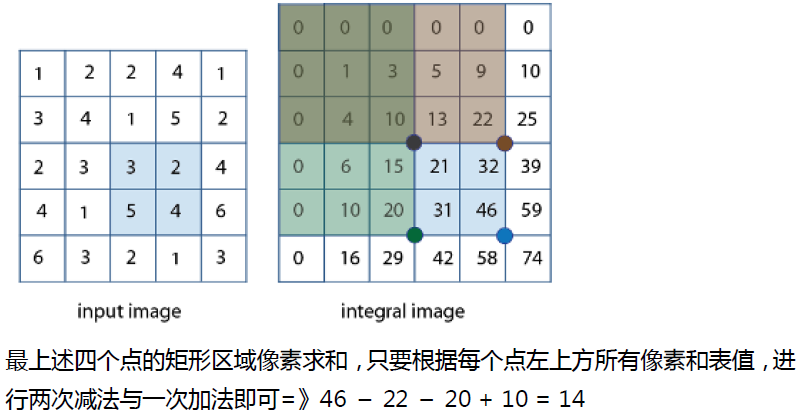
2 所用到的主要OpenCv API

*

3 程序代码

#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
void blur_demo(Mat &image, Mat &sum);
void edge_demo(Mat &image, Mat &sum);
int getblockSum(Mat &sum, int x1, int y1, int x2, int y2, int i);
int main(int argc, char** argv) {
    Mat src = imread("images/lena.png");
    if (src.empty()) {
        printf("could not load image...\n");
        return -1;
    }
    namedWindow("input", CV_WINDOW_AUTOSIZE);
    imshow("input", src);
    namedWindow("output", CV_WINDOW_AUTOSIZE);
    // 计算积分图
    Mat sum, sqrsum;
    integral(src, sum, sqrsum, CV_32S, CV_32F);
    // 积分图应用
    int type = 0;
    while (true) {
        char c = waitKey(100);
        if (c > 0) {
            type = (int)c;
            printf("c : %d\n", type);
        }
        if (c == 27) {
            break; // ESC
        }
        if (type == 49) { // 数字键 1
            blur_demo(src, sum);
        }
        else if (type == 50) { // 数字键 2
            edge_demo(src, sum);
        }
        else {
            blur_demo(src, sum);
        }
    }
    waitKey(0);
    return 0;
}
void blur_demo(Mat &image, Mat &sum) {
    int w = image.cols;
    int h = image.rows;
    Mat result = Mat::zeros(image.size(), image.type());
    int x2 = 0, y2 = 0;
    int x1 = 0, y1 = 0;
    int ksize = 5;
    int radius = ksize / 2;
    int ch = image.channels();
    int cx = 0, cy = 0;
    for (int row = 0; row < h + radius; row++) {
        y2 = (row + 1)>h ? h : (row + 1);
        y1 = (row - ksize) < 0 ? 0 : (row - ksize);
        for (int col = 0; col < w + radius; col++) {
            x2 = (col + 1)>w ? w : (col + 1);
            x1 = (col - ksize) < 0 ? 0 : (col - ksize);
            cx = (col - radius) < 0 ? 0 : col - radius;
            cy = (row - radius) < 0 ? 0 : row - radius;
            int num = (x2 - x1)*(y2 - y1);
            for (int i = 0; i < ch; i++) {
                // 积分图查找和表，计算卷积
                int s = getblockSum(sum, x1, y1, x2, y2, i);
                result.at<Vec3b>(cy, cx)[i] = saturate_cast<uchar>(s / num);
            }
        }
    }
    imshow("output", result);
    imwrite("D:/result.png", result);
}
/**
* 3x3 sobel 垂直边缘检测演示
*/
void edge_demo(Mat &image, Mat &sum) {
    int w = image.cols;
    int h = image.rows;
    Mat result = Mat::zeros(image.size(), CV_32SC3);
    int x2 = 0, y2 = 0;
    int x1 = 0, y1 = 0;
    int ksize = 3; // 算子大小，可以修改，越大边缘效应越明显
    int radius = ksize / 2;
    int ch = image.channels();
    int cx = 0, cy = 0;
    for (int row = 0; row < h + radius; row++) {
        y2 = (row + 1)>h ? h : (row + 1);
        y1 = (row - ksize) < 0 ? 0 : (row - ksize);
        for (int col = 0; col < w + radius; col++) {
            x2 = (col + 1)>w ? w : (col + 1);
            x1 = (col - ksize) < 0 ? 0 : (col - ksize);
            cx = (col - radius) < 0 ? 0 : col - radius;
            cy = (row - radius) < 0 ? 0 : row - radius;
            int num = (x2 - x1)*(y2 - y1);
            for (int i = 0; i < ch; i++) {
                // 积分图查找和表，计算卷积
                int s1 = getblockSum(sum, x1, y1, cx, y2, i);
                int s2 = getblockSum(sum, cx, y1, x2, y2, i);
                result.at<Vec3i>(cy, cx)[i] = saturate_cast<int>(s2 - s1);
            }
        }
    }
    Mat dst, gray;
    convertScaleAbs(result, dst);
    normalize(dst, dst, 0, 255, NORM_MINMAX);
    cvtColor(dst, gray, COLOR_BGR2GRAY);
    imshow("output", gray);
    imwrite("D:/edge_result.png", gray);
}
int getblockSum(Mat &sum, int x1, int y1, int x2, int y2, int i) {
    int tl = sum.at<Vec3i>(y1, x1)[i];
    int tr = sum.at<Vec3i>(y2, x1)[i];
    int bl = sum.at<Vec3i>(y1, x2)[i];
    int br = sum.at<Vec3i>(y2, x2)[i];
    int s = (br - bl - tr + tl);
    return s;
}

4 运行结果

5 扩展及注意事项

6*目前只做大概了解，知道有这一算法，后续具体使用再做具体分析