AT abc144
A
B
C
题意
- 矩阵 \((i,j)\) 位置的数是 \(i*j\) 。最初站在 \((1,1)\) 的位置,可以向 \((i+1,j)\) 和 \((i,j+1)\) 走,问走到位置是 \(n\) 的位置需要的最小步数
思路
- 权值是 \(n\) 的位置,有 \(n\) 的因数个,求这些因数中和最小的一对,输出他们的最小和-2
D
题意
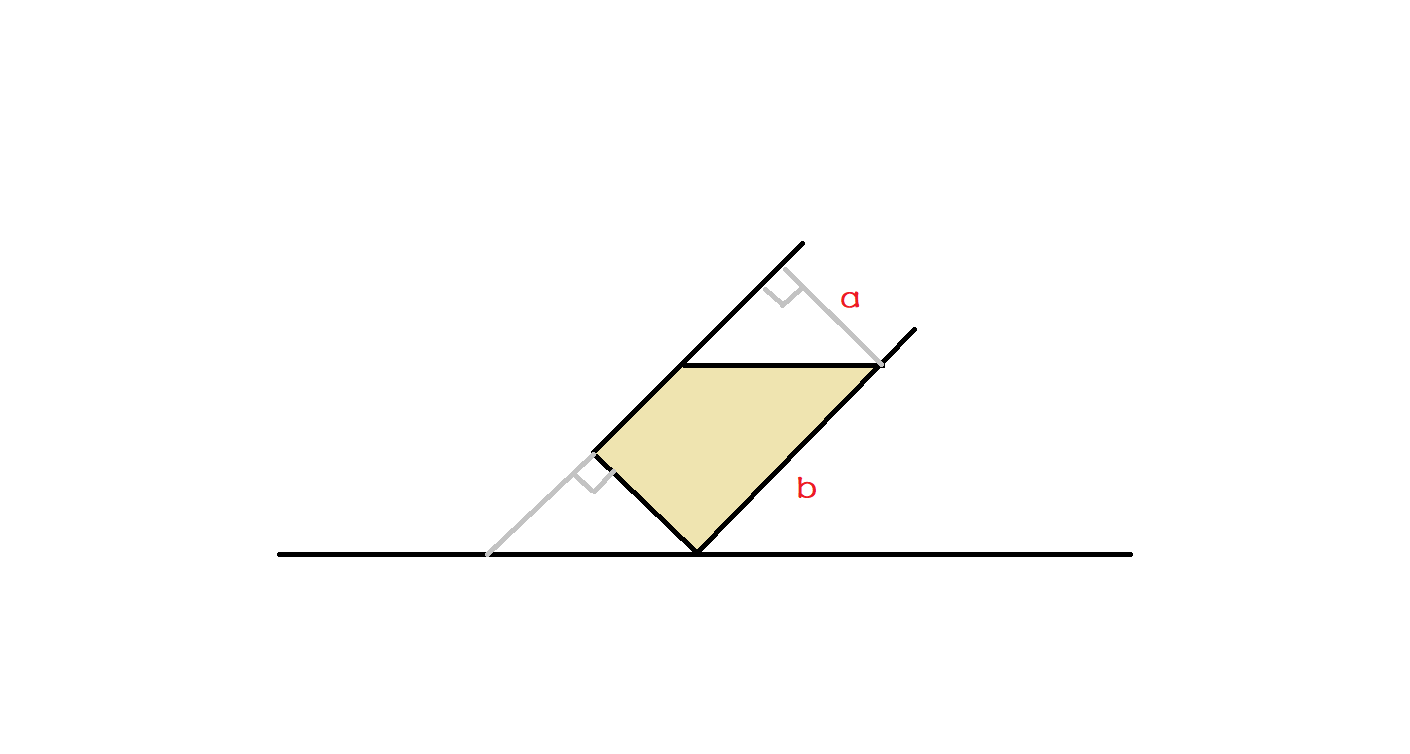
- 给你一个立方体的容器,底部的正方形边长是 \(a\) ,高是 \(b\) 。里边有 \(x\) 体积水。使杯子倾斜但不让水流出,问可偏转的最大角度
思路
- 有两种情况。
- 一种是杯底露出。一种是杯底不露出。
- 对于杯底露出的情况。水的形状是一个三棱柱。我们可以根据水的体积和底边长求出三角形的面积,三角形一直角边是杯子的高,求出另一直角边,求出正切值。根据反三角函数求出角度。
- 对于杯底不露出的情况。水的形状是一个多棱柱,高还是底边边长,底面变成一个长方形和一个三角形,按高和底面长补成一个长方形。这个长方形的面积可求,多余的小三角形的面积也可求。这个小三角形一直角边已知,另一直角边可求,求出正切值,根据反三角求出角度
小结
- 反三角函数 \(atan(),acos(),asin()\)
- 返回值是弧度制
- \(\pi=acos(-1.0)\)
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
double a,b,x,s;
int main(){
cin>>a>>b>>x;
s=x/a;
double pi=acos(-1.0);
if(2.0*s<a*b){
double opt=a*b*b/(2.0*x);
double now=atan(opt);
double ans=now/pi*180;
printf("%.10lf",ans);
}
else {
double opt=(double)2.0*b/a-2.0*x/a/a/a;
double now=atan(opt);
double ans=now/pi*180;
printf("%.10lf",ans);
}
}
E
题意
- 给定两个序列 \(A,F\) 。求最大的 \(A_i\cdot F_i\) 最小。但是我们可以对任意的 \(A_i\) 减掉任意数值,但减掉的数的总和不超过 \(K\)。
- \(K\leq10^{18}\)
思路
- 首先如果没有删除操作的话,我们直接一个从大到小,一个从小到大排序可。
- 现在有删除操作。
- 我们可以二分答案,对于大于所二分的积,我们求出需要减掉的值的和,check也很简单
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<map>
#define ll long long
using namespace std;
int n,m;
ll k;
int a[1000005],b[1000005];
struct node{
int a,b;
ll v;
}d[1000005];
bool check(ll now){
ll s=0;
for(int i=1;i<=n;i++)
if(d[i].v>now){
s=s+(ll)d[i].a-now/d[i].b;
// else s=s+(ll) d[i].a-now/d[i].b;if(now%d[i].b==0)
}
if(s<=k) return true;
return false;
}
int main(){
scanf("%d%lld",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int j=1;j<=n;j++) scanf("%d",&b[j]);
sort(a+1,a+n+1);
sort(b+1,b+n+1);
for(int i=1;i<=n;i++) d[i].v=1ll*a[i]*b[n-i+1],d[i].a=a[i],d[i].b=b[n-i+1];
ll l=0,r=1e18,ans=0;
while(l<=r){
ll mid=(l+r)/2;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld",ans);
return 0;
}
F



