ZR普转提day1
A
- CF的原题
- 给定一个数字串,让你删掉它的一个连续子串使的剩下的没有重复元素
- 枚举要删掉子串的起点,在起点之前必须保证没有重复元素。并把这些元素存入vector,接下来找它的终点,倒着找,如果这个元素出现了两次,肯定要删掉这个元素,终点也就找到了
C
- DP
- 先从暴力写挂的原因写起吧,其实对于物品的顺序已经规定好了,我们只需要考虑是不是选这个物品就好了,我们就枚举每个选还是不选。是 \(2^n\) 的。选完之后,check。考试时,是爆搜之前的排序顺序错了
- 应该是进入时间相同的,出来时间大的在前
- 正解的排序方法是按出来时间从小到大排序,如果出来时间相同就按进入时间大的在前。这样保证,在它前边的物品一定在它上边。
- 我们设 \(f[i][j]\) 表示 \(i\) 这个物品及其上边的物品在任何时刻最大承重是 \(j\) 所获得的最大收益
- 那么 \(i\) 这个物品转移的状态只有 $a[i].in $ 和 \(a[i].out\) 这个范围内,因为只有在这个范围内才保证是其上边的物品,在它前边但不相交的物品,是在它进入之前就已经进去又出去了,所以不能用它转移
- 还设 \(h[u][j]\) 表示 在 \(i\) 这个物品在背包的时间内, 到 \(u\) 这个时间点,最大限重不超过 \(j\) 的 \(f\) 的前缀和最大
- 这个数组的意义
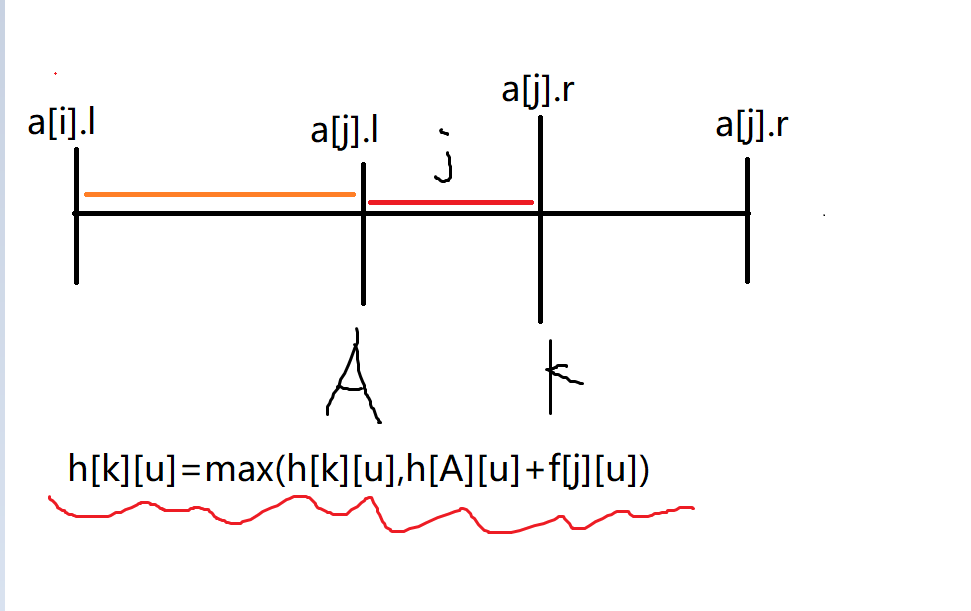
- 为了算上A之前的物品
代码AC
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int n,S,ans;
int f[505][1002],h[1005][1002];
struct node{
int in,out,s,w,v;
}a[505];
bool cmp(node a,node b){
if(a.out ==b.out ) return a.in >b.in ;
return a.out <b.out ;
}
int main()
{
scanf("%d%d",&n,&S);
for(int i=1;i<=n;i++) scanf("%d%d%d%d%d",&a[i].in,&a[i].out,&a[i].w,&a[i].s,&a[i].v);
a[n+1].out =n*2;
a[n+1].s =S;
n++;
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++){
int up=min(a[i].s ,S-a[i].w),j=1;
memset(h,0,sizeof(h));
while(a[j].out <=a[i].in &&j<n) j++;//排除这个物品之外的物品
for(int k=a[i].in+1;k<=a[i].out;k++){
memcpy(h[k],h[k-1],sizeof(h[k]));
for(;a[j].out ==k&&j<i;j++){
int x=a[j].in ;
if(x<a[i].in ) continue;
for(int u=0;u<=up;u++) h[k][u]=max(h[k][u],h[x][u]+f[j][u]);
}
}
for(int t=0;t<=up;t++) f[i][t+a[i].w]=h[a[i].out][t]+a[i].v ;
for(int u=1;u<=S;u++) f[i][u]=max(f[i][u],f[i][u-1]);
}
printf("%d",f[n][S]);
return 0;
}
暴力代码20
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int n,s,ans,nn;
int p[505];
struct node{
int pin,pout,w,s,v,nowei;
}e[505],ton[505];
bool cmp(node a,node b){
if(a.pin ==b.pin ) return a.pout >b.pout ;
return a.pin <b.pin ;
}
void cal(int x){
int jus=0,res=0;
for(int i=0;i<=2*n;i++){
while(ton[res].pout==i&&res>0) {
jus=jus+ton[res].v;
ans=max(ans,jus);
res--;
}
if(ton[res].pout <i&&res) return ;
for(int j=0;j<x;j++){
if(e[p[j]].pin!=i) continue;
for(int k=1;k<=res;k++){
ton[k].nowei+=e[p[j]].w ;
if(ton[k].nowei >ton[k].s ||ton[k].nowei >s) return ;
}
ton[++res]=e[p[j]];
// for(int i=1;i<=res;i++) printf("%d ",ton[i].nowei );
}
// cout<<endl;
}
ans=max(ans,jus);
}
void dfs(int now,int cnt){
if(now==n){
cal(cnt);
return ;
}
for(int i=now+1;i<=n;i++){
p[cnt]=i;
dfs(i,cnt+1);
p[cnt]=0;
}
}
int main()
{
scanf("%d%d",&n,&s);
for(int i=1;i<=n;i++) {
scanf("%d%d%d%d%d",&e[i].pin,&e[i].pout,&e[i].w,&e[i].s,&e[i].v);
nn=max(nn,e[i].pout);
}
sort(e+1,e+n+1,cmp);
// for(int i=1;i<=n;i++) printf("%d %d\n",e[i].pin ,e[i].pout );
// cout<<endl;
dfs(0,0);
printf("%d",ans);
return 0;
}
D
- \(n\) 个盒子看成 \(n\) 个二进制数, 二进制的位数是 \(m\) 。\(0,1\) 代表有没有
- 我们最终的答案是 \(2^m-1\) 这种状态的方案数
- 考虑递推
- 我们设 \(g[i]\) 表示 一种二进制状态转成十进制数 \(i\) 的个数,也就是统计这\(n\) 个状态中每种状态的个数
- 设 \(G[i]\) 表示 \(i\) 这种状态及其子集的 个数
- 设 \(f[i]\) 表示并集为 \(i\) 及其子集的方案数
\(f[i]=2^{G[i]}\)
- 相当于这 \(G[i]\) 个状态为 \(i\) 的所有子集(包括全集,选还是不选,也就是拼全是1的过程,当然除了全集其他状态都不合法
- 所以,我们只要去掉 \(f[i]\) 中所有子集,只留下全集就是答案了
- 我们求 \(f\) 时是求 \(g\) 的所有子集,现在我们要去掉 \(f\) 的所有子集,只要求出来减一下就好了
- 关键是如何求出一个集合的子集个数
- 设集合 \(A=111\) 它的子集有 {001},{010},{100},{011},{101},{110},
- 如果这一位是1 我们可以改成0 其他位不变就是它的子集,它的子集的二进制一定比它小,因为我们是递推比他小的答案已经算过了,所以直接算就行。
代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#define ll long long
using namespace std;
const ll MOD=1e9+7;
int n,m;
ll p[10000005];
ll g[10000006],f[10000005];
int main()
{
scanf("%d%d",&n,&m);
int up=(1<<m)-1;
for(int i=1;i<=n;i++){
int num,x,res=0;
scanf("%d",&num);
for(int j=1;j<=num;j++){
scanf("%d",&x);
x--;
res|=(1<<x);
}
g[res]++;
}
for(int i=0;i<=m;i++)
for(int j=0;j<=up;j++)
if(j&(1<<i)) g[j]+=g[j^(1<<i)];
p[0]=1;
for(int i=1;i<=n;i++) p[i]=(p[i-1]<<1)%MOD;
for(int i=0;i<=up;i++) f[i]=p[g[i]];
for(int i=0;i<=m;i++)
for(int j=0;j<=up;j++)
if(j&(1<<i)) f[j]=(f[j]-f[j^(1<<i)]+MOD)%MOD;
printf("%lld",f[up]);
return 0;
}

