P4557 [JSOI2018]战争
给出两个凸包。之后有q个询问问你第一个凸包加上给出的向量会不会与第二个凸包有交点。
这里假设A为第一个凸包的点集,B为第二个凸包的点击,p为移动的向量。
那么由题意可以得到: A + p = B, 将式子稍微变形可以得到这个移动向量的范围,即p = B - A
参考链接:https://www.cnblogs.com/xzyxzy/p/10229921.html
这里引入一个几何概念:
闵可夫斯基和:定义F(A, B)为闵可夫斯基和
F(A, B) = {(ai+bi, aj+bj)| Vai属于A, Vbi属于B}
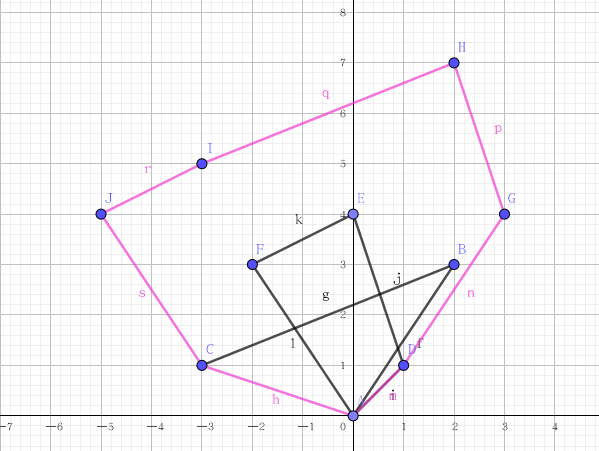
通俗一点:就是将一个多边形的一个点定到另一个多边形上,之后定点绕着多边形移动所画出的区域就是。
图片来源于:上面的博客。
这里还需要一个二分判断点是否在凸包内的。
具体的思想就是叉积,两条线的叉积能确定线的相对位置,所以可以二分。
以下是代码:

#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; typedef long long ll; struct Point { ll x, y; Point(){x=y=0;} Point(ll _x, ll _y):x(_x),y(_y){} Point operator-(const Point& _p) const{return Point(x-_p.x, y-_p.y);} Point operator+(const Point& _p) const{return Point(x+_p.x, y+_p.y);} ll operator*(const Point& _p) const{return x * _p.x + y * _p.y;} ll operator^(const Point& _p) const{return x*_p.y - y*_p.x;} void input(){scanf("%lld%lld", &x, &y);} /*sort*/ bool operator==(const Point& _p) const{return x==_p.x&&y==_p.y;} bool operator<(const Point& _p) const{return x==_p.x ? y<_p.y : x<_p.x;} } A[N], B[N], C[N]; ll cro(Point a, Point b, Point c) {return (b-a) ^ (c-a);} ll dot(Point a, Point b, Point c) {return (b-a) * (c-a);} int ConvexHull(Point *p, int n, Point* ch, int flag=1) { sort(p, p+n); //先比较x坐标,再比较y坐标 if (flag) n = unique(p, p+n)-p; int m = 0; for (int i = 0; i < n; ++ i) { while (m > 1 && cro(ch[m-2], ch[m-1], p[i]) < flag) -- m; ch[m++] = p[i]; } int temp = m; for (int i = n - 2; i >= 0; -- i) { while (m > temp && cro(ch[m-2], ch[m-1], p[i]) < flag) -- m; ch[m++] = p[i]; } return m -= (n > 1); } //点在线段上(包含端点),在为 1 ,不在为 0 bool isPointOnSegment(Point P,Point A,Point B) { return cro(P, A, B) == 0 && dot(P, A, B) <= 0; // 不包含端点时为 <0 } //判断点在凸包内模板 O(logn) //凸包为逆时针 //在边界,返回0,在内部,返回1,在外部,返回-1 int check(Point A, Point*p, int n ) { if (isPointOnSegment(A, p[0], p[1])) return 0; // 包含端点 if (isPointOnSegment(A, p[0], p[n-1])) return 0; int l = 1, r = n - 2, mid; while (l <= r) { mid = l + r >> 1; ll a1 = cro(p[0], p[mid], A); ll a2 = cro(p[0], p[mid+1], A); if (a1 >= 0 && a2 <= 0) { ll tmp = cro(p[mid], p[mid+1], A); if (tmp > 0)return 1; if (tmp == 0) return 0; return -1; } else if (a1 < 0) r = mid - 1; else l = mid + 1; } return -1; } int Minkowski(Point *A, int n, Point *B, int m, Point *C){ int t = 0, x = 1, y = 1; C[t++] = A[0] + B[0]; A[n] = A[0], B[m] = B[0]; while (x <= n && y <= m) if ( ((A[x]-A[x-1]) ^ (B[y]-B[y-1])) > 0) C[t] = C[t-1] + A[x] - A[x-1], t ++, x ++; else C[t] = C[t-1] + B[y] - B[y-1], t ++, y ++; while (x <= n) C[t] = C[t-1] + A[x] - A[x-1], t ++, x ++; while (y <= m) C[t] = C[t-1] + B[y] - B[y-1], t ++, y ++; return t - 1; } int main() { // freopen("in.txt", "r", stdin); // freopen("out.txt", "w", stdout); int n, m, q; scanf("%d%d%d", &n, &m, &q); for (int i = 0; i < n; ++ i) A[i].input(); for (int i = 0; i < m; ++ i) B[i].input(), B[i].x *= -1, B[i].y *= -1; n = ConvexHull(A, n, C); memcpy(A, C,sizeof(Point)*(n)); m = ConvexHull(B, m, C); memcpy(B, C,sizeof(Point)*(m)); int p = Minkowski(A, n, B, m, C); for (int i = 0; i < q; ++ i) { Point temp; temp.input(); puts(check(temp, C, p) == -1 ? "0" : "1"); } return 0; }
这里有个小知识: 闵可夫斯基和凸包上的点等于向量种类数





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· winform 绘制太阳,地球,月球 运作规律
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
2020-03-09 简单绘制复杂图形
2020-03-09 箭头的绘制
2020-03-09 中国加油
2020-03-09 渐变彩条
2020-03-09 自适应图形的绘制
2020-03-09 红色椭圆、蓝色正方形、黄色三角形、紫色五角星