表达式树

表达式树生成代码（源自紫书）：

#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 100;
const int maxm = 1e6 + 100;
const int inf = 0x3f3f3f3f; //1061109567

//结点左右编号和字符
int lch[maxn], rch[maxn];
char op[maxn];
int nc; // 结点数

//表达式树的每一个非叶结点都代表了运算符，
//每一棵子树都是一条运算式

//表达式树中序遍历就是最开始的表达式
//后序遍历就是后缀表达式
//先序遍历就是前缀表达式

int build_tree(char * s, int x, int y) {
    int i, c1 = -1, c2 = -1, p = 0;
    int u;
    if (y - x == 1) { //仅一个字符，建立单独节点
        u = ++ nc;
        lch[u] = rch[u] = 0;
        op [u] = s[x];
        return u;
    }
    for (int i = x; i < y; ++ i) {
        switch (s[i]) {
        case '(': p ++; break;
        case ')': p --; break;
        case '+': case '-': if(!p) c1=i; break;
        case '*': case '/': if(!p) c2=i; break;
       }
    }
    if (c1 < 0) c1 = c2; //找不到括号外的加减号就用乘除号。
    if (c1 < 0) return build_tree(s, x+1, y-1);
    u = ++nc;
    lch[u] = build_tree(s, x, c1);
    rch[u] = build_tree(s, c1+1, y);
    op[u] = s[c1];
    return u;
}
int main()
{
    cin.tie(0);
    ios::sync_with_stdio(0);
    char s[100];
    scanf("%s", s);
    build_tree(s, 0, strlen(s));

    return 0;
}

关于表达式求值（引自OI Wiki）：

我个人更喜欢非递归方式求值。

非递归的方法是定义两个 栈 来分别存储运算符和运算数。每当遇到一个数直接放进数的栈；每当遇到一个操作符时，要查找之前运算符栈中的元素，按照预先定义好的优先级来进行适当的弹出操作（弹出的同时求出对应的子表达式的值）。

我们要知道：算术表达式分为三种，分别是前缀表达式、中缀表达式、后缀表达式。

其中，中缀表达式是我们日常生活中最常用的表达式；后缀表达式是计算机最容易理解的表达式。

为什么说后缀表达式最容易被计算机理解呢？因为后缀表达式不需要括号表示，它的运算顺序是唯一确定的。

举个例子：在后缀表达式 32 * 1 - 中，首先计算 3 X 2 = 6 （使用最后一个运算符，即栈顶运算符），然后计算  6 - 1 = 5。

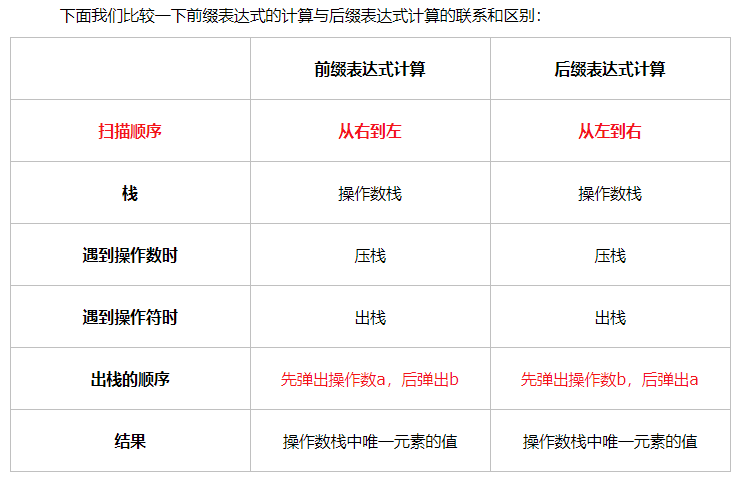
可以看到：对于一个后缀表达式，只需要 维护一个数字栈，每次遇到一个运算符，就取出两个栈顶元素，将运算结果重新压入栈中 。

最后，栈中唯一一个元素就是改后缀表达式的运算结果时间复杂度 O(n)。

 

所以说，对于普通中缀表达式的计算，我们可以将其转化为后缀表达式再进行计算。转换方法也十分简单。只要建立一个用于存放运算符的栈，扫描该中缀表达式：

1. 如果遇到数字，直接将该数字输出到后缀表达式（以下部分用「输出」表示输出到后缀表达式）；
2. 如果遇到左括号，入栈；
3. 如果遇到右括号，不断输出栈顶元素，直至遇到左括号（左括号出栈，但不输出）；
4. 如果遇到其他运算符，不断去除所有运算优先级大于等于当前运算符的运算符，输出。最后，新的符号入栈；
5. 把栈中剩下的符号依次输出，表达式转换结束。

时间复杂度O(n)。

 

 顺便放一个嫖来的代码（Uva12219）：

#define _CRT_SECURE_NO_WARNINGS 
#include<iostream>
#include<algorithm>
#include<string>
#include<sstream>
#include<set>
#include<vector>
#include<stack>
#include<map>
#include<queue>
#include<deque>
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>
#include<functional>
using namespace std;
 
const int mx = 60000;
int T, rnd, cnt;
char expr[mx * 5], *p;
int done[mx];
struct Node
{
    string s;
    int ha, left, right;
    bool operator < (const Node&b)const//由于下面要用到map::count函数，所以必须要重载小于号
    {
        if (ha != b.ha)return ha < b.ha;
        if (left != b.left)return left < b.left;//哈希相同则比较出现的顺序
        return right < b.right;
    }
}node[mx];
map <Node, int>dict;//记录子树的编号
int solve()
{
    int id = cnt++;//从0开始编号
    Node&u = node[id];
    u.left = u.right = -1;
    u.s = "";
    u.ha = 0;
    while (isalpha(*p))
    {
        u.ha = u.ha * 27 + *p - 'a' + 1;//可以理解为27进制，a到z的编号为1到26
        u.s.push_back(*p);//将该子树的字母放入s
        p++;//向后扫描，遇到括号停止
    }
    if (*p == '(')//(L,R)，递归处理左右子树
    {
        p++;//先跳过'('
        u.left = solve(), p++;//返回左子树编号，并跳过','
        u.right = solve(),p++;//返回右子树编号，并跳过')'
    }
    if (dict.count(u))
    {
        cnt--;//子树出现过，个数减少1
        return dict[u];//返回这颗子树的编号
    }
    return dict[u] = id;//如果这棵树是首次出现，给它编号
}
void print(int v)
{
    if (done[v] == rnd)printf("%d", v + 1);//已经输出过了，输出序号即可
    else
    {
        done[v] = rnd;//不需要对done数组初始化，只需要用这一轮特有的rnd标记即可
        printf("%s", node[v].s.c_str());//输出树根的字母
        if (node[v].left != -1)//含有左右子树
        {
            putchar('(');
            print(node[v].left);//递归输出左右子树
            putchar(',');
            print(node[v].right);
            putchar(')');
        }
    }
}
 
int main()
{
    freopen("test.txt", "r", stdin);
    scanf("%d", &T);
    for (rnd = 1; rnd <= T;rnd++)
    {
        dict.clear();
        cnt = 0;
        scanf("%s", expr);
        p = expr;//用指针p扫描expr
        print(solve());
        putchar(10);//打印换行符
    }
    return 0;
}