约瑟夫环以及其变种集合
最近在CF上补题，补到了一道关于约瑟夫环的题目（听都没听过，原谅我太菜）
就去好好学了一下，不过一般的题目应该是不会让你模拟过的，所以这次就做了一个约瑟夫环公式法变形的集合。
关于约瑟夫环的基础讲解，我个人认为最好的就是这篇了。
首先是最原始的约瑟夫环的题目：
https://vjudge.net/problem/51Nod-1073（小数据规模）
#include <bits/stdc++.h> using namespace std; int main() { ios::sync_with_stdio(0); cin.tie(0); int n, m; int s = 0; cin >> n >> m; for (int i = 2; i <= n; i++) s = (s + m) % i; cout << s + 1 << endl; return 0; }
解题思路：
没啥好讲的直接套公式即可。
https://vjudge.net/problem/51Nod-1074（大数据规模）
#include <bits/stdc++.h> using namespace std; typedef long long ll; int main() { ios::sync_with_stdio(0); cin.tie(0); ll n, m; ll ans = 0; cin >> n >> m; for (ll i = 2; i <= n; i++) { if (ans + m < i) { ll len = (i - ans) / m; if (len + i < n) { i += len; ans += m*len; } else { ans += m*(n-i); i = n; } } ans = (ans + m) % i; } cout << ans + 1 << endl; return 0; }
解题思路：
除去超大的n之外。就是个约瑟夫环的裸题。
约瑟夫环递推公式，n为人数，m为步长。
f(1) = 0
f(n) = [f(n-1)+m]%i i∈[2,n]
基本约瑟夫环优化就是当k=1的时候，每次递推就是在+1，可以直接算出来快速跳过，f(n)=f(1)+n-1
当n超大的时候，可以照着这种思路快速简化递推过程。在递推后期，f(x)+m在很长的周期内<i，假设有len个周期，
那么这些周期合并后的结果相当于f(x)+len*m。可以快速跳过。条件限制是: f(x)+len*m<i+(len-1)
可以推出来：
当len=1时，条件限制: f(x)+m<i
当len=2是，条件限制: f(x+1)+m<i+1=f(x)+2*m<i+1
当m=m时，条件限制：f(x)+len*m<i+(len-1)
化简有m<(i-f(x)-1)/(len-1)，若能整除，就是(i-f(x)-1)/(m-1)-1，否则就是(i-f(x)-1)/(m-1)直接取整。
这样，i+=len，f(x)+=m*len，快速跳过了中间过程。
若i+len>n，说明快速跳越界了，这时候可以直接算出f(n)=f(x)+(n-i-1)*len。
但其实还有种更快的做法，但是我太菜看不懂，希望看懂的巨巨能教教我。
#include<bits/stdc++.h> using namespace std; long long n, m, ans; int t; int main() { scanf("%d", &t); while(t--) { scanf("%lld%lld", &n, &m); ans = n * m; while(ans > n) ans = ans - n + (ans - n - 1) / (m - 1); printf("%d\n", ans); } return 0; }
约瑟夫环变形问题一：
一圈共有N个人，开始报数，第i轮报到i的人自杀，然后重新开始报数，问最后自杀的人是谁？
思路：和原本的约瑟夫环问题的唯一区别是：m值不在固定。同样的我们将最后一位自杀者叫做p，那么在前一轮(第x轮)中的自杀者所报的号为x-1,第x轮中p的报号为x，如此下去……
得出公式：f(n) = (f(n-1) + n-(i-1)) % i，i∈[2,n] 其实我加粗的部分就是每一轮的步长(第一轮是1，第二轮是2···第六轮是6)，因为正过程是-，所以逆过程是+。
题目链接：https://vjudge.net/problem/HDU-5643
#include <bits/stdc++.h> using namespace std; typedef long long ll; int main() { ios::sync_with_stdio(0); cin.tie(0); int t; cin >> t; while (t--) { int n; cin >> n; int ans = 0; for (int i = 2; i <= n; i++) { ans = (ans + n - (i-1)) % i; } cout << ans + 1 << endl; } return 0; }
约瑟夫环变形问题二：
一圈共有N个人，第一轮杀死了S，之后从S+1开始报数，每轮报到M的人自杀，然后重新开始报数，问最后自杀的人是谁？
思路：和原本的约瑟夫环问题的唯一区别是：开始给了一个S值，那么我们只需要在按原始约瑟夫环处理2到n-1轮之后，再加上s对n取余即可。
(这个也十分好想，因为按照原来的约瑟夫环思路，那么应该是从0开始的，但是现在从s开始了，相当于所有的坐标都向前移了s。
题目链接：https://vjudge.net/problem/UVA-1394
#include <bits/stdc++.h> using namespace std; typedef long long ll; int main() { ios::sync_with_stdio(0); cin.tie(0); int n, m, k; while (cin >> n >> m >> k && (n&&k&&m)) { int ans = 0; for (int i = 2; i < n; i++) ans = (ans + m) % i; ans = (ans + k) % n; cout << ans + 1 << endl; } return 0; }
注意这种类型的题目还有一种形式，便是从s开始报数，而不是第一轮杀死了s。这样的话就处理到2到n轮，再加上s对n取余即可。
约瑟夫环变形问题三：
一圈共有N个人，第一轮杀死了S，之后从S+1开始报数，每轮报到M的人自杀，然后重新开始报数，问每一轮自杀的人是谁？（按顺序输出）
思路：最基础的就是模拟链表或者队列来获得顺序，但是我在网上还看到了一种更为“酷”的方法——树状数组/线段树
链接：https://blog.csdn.net/no1_terminator/article/details/51820165 （这篇博客有一点不足就是没有讲为啥这样为啥想到这样
我就以问答以及点评的方式来解决上面这篇博客的不足吧。
Q1:为什么会想到用树状数组呢？
A1:因为要输出顺序的话需要一直维护前缀和所以我们就想到了用树状数组。
Q2:为什么需要用到前缀和呢？
A2:因为前缀和可以很直观的表示当前位置以及之前有多少个人存活。
那为什么需要当前位置之前有多少个人存活呢？是因为 (上轮出去的人 + k - 1) % 当前存活人数 正好等于这轮要出去的人之前存活了多少人（这就和前缀和联系起来了
现在可以模拟一下过程。(特地给出与上面那篇博客不一样的例子帮助理解
假设n = 7, k = 4, s = 1(s是从s开始报数)
那么就可以得到最初的前缀和数组，如下图（从1开始
我们需要一个中间变量来帮助计算，那么我们设temp = s
temp = (temp + 4 - 1) % 7 = （1 + 4 - 1） % 7 = 4(这里为啥是k-1是因为当这轮结束之后就需要从当前位置的下一个人开始报数。-1是为了抵消下一个人开始报数带来的影响）
所以这一轮出去的是前面存活4个人的人。用树状数组查询前缀和为4的第一个位置，将其push_back进输出ans数组（可以想想啥要第一个位置
同时在4的位置-1，并维护前缀和数组
这轮结束之后temp = 4， ans: 4
接下来就比较简单了。就是一直重复而已
temp = (temp + 4 - 1) % 6 = (4 + 4 - 1) % 6 = 1
找到前缀和为1的第一个位置，将其push_back进输出数组，再将1的位置-1，维护前缀和数组
这轮结束之后temp = 1, ans: 4 1
temp = (temp + 4 - 1) % 6 = (1 + 4 - 1) % 5 = 4
找到前缀和为4的第一个位置，将其push_back进输出数组，再将前缀和为4的位置-1，维护前缀和数组
这轮结束之后temp = 4, ans: 4 1 6
temp = (temp + 4 - 1) % 6 = (4 + 4 - 1) % 4 = 3
找到前缀和为3的第一个位置，将其push_back进输出数组，再将前缀和为3的位置-1，维护前缀和数组
这轮结束之后temp = 3, ans: 4 1 6 5
temp = (temp + 4 - 1) % 6 = (3 + 4 - 1) % 3 = 0 注意这里出现了模运算之后为0的情况，这种情况的时候就直接使其等于存活人数即可
找到前缀和为3的第一个位置，将其push_back进输出数组，再将前缀和为3的位置-1，维护前缀和数组
这轮结束之后temp = 3, ans: 4 1 6 5 7
temp = (temp + 4 - 1) % 6 = (3 + 4 - 1) % 2 = 0
找到前缀和为2的第一个位置，将其push_back进输出数组，再将前缀和为2的位置-1，维护前缀和数组
这轮结束之后temp = 2, ans: 4 1 6 5 7 3
最后一轮不在赘述，至此ans: 4 1 6 5 7 3 2，推导完毕
这里给一道题目：https://vjudge.net/problem/OpenJ_Bailian-3254（这道模拟也是能过的。但是建议复习一下刚学的知识！）
#include <bits/stdc++.h> #define maxn 1000000 using namespace std; int bit[maxn]; int n,k, m; int sum(int i){ int s=0; while (i>0){ s+=bit[i]; i-=(i&(-i)); } return s; } void add(int i,int x){ while (i<=n){ bit[i]+=x; i+=(i&(-i)); } } int binary_search(int id){ int l=0,r=n+1; while (l<r){ int mid=(l+r)>>1; if (sum(mid)<id)l=mid+1; else r=mid; } return l; } int main(){ ios::sync_with_stdio(0); cin.tie(0); while (cin >> n >> m >> k){ if (!n && !k && !m) break; int id=m; memset(bit,0,sizeof(bit)); for (int i=1;i<=n;i++) add(i,1); for (int i=1;i<=n;i++){ id=(id+k-1)%(n-i+1); if (!id) id = n-i+1; int newid=binary_search(id); if (i == 1) cout << newid; else cout << "," << newid; add(newid,-1); } cout << endl; } return 0; }
约瑟夫环变形问题四：
一圈共有N个人，从第一个人开始报数，每轮报到M的人自杀，然后重新开始报数，问最后三个人是谁？（按顺序输出）
题目链接：https://vjudge.net/problem/UVA-1452
解题思路：
可以用变形问题四的方法解，在此不再赘述。这里讲一下公式法的方法。
首先我们知道公式法每一次计算的值代表的是每轮重新计数后最后存活者的下标，所以我们倒推回去可以得到一开始的最后存活的下标。
我们知道最后一轮存活者的下标为当前轮的0位置
倒数第二轮的自杀者的下标为当前轮的1位置
倒数第三轮的自杀者的下标为当前轮的2位置
（具体可以看下图）
所以我们只需要把三个变量单独拎出来进行三次循环即可。当然也可以将三个变量放在一个循环里。这里为了便于理解就分开来了。
AC代码：
#include <bits/stdc++.h> using namespace std; int f[500000 + 100], N, K; int main() { int T, i; cin >> T; while (T--) { cin >> N >> K; int i; f[2]=2; for(i=3;i<=N;i++)f[i]=(f[i-1]+K)%i; cout << f[N]+1 << " "; f[1]=1; for(i=2;i<=N;i++)f[i]=(f[i-1]+K)%i; cout << f[N]+1 << " "; f[0]=0; for(i=1;i<=N;i++)f[i]=(f[i-1]+K)%i; cout << f[N]+1 << endl; } }
约瑟夫环变形问题五：
一圈共有N个人，从第一个人开始报数，每轮报到M的人自杀，希望最后一个出局的人的位置是S，那么最小的M是多少（反约瑟夫环）
解题思路：这种题目目前好像没啥较为快速的解法。只能是爆枚举加暴力check，如果以后看到较为快速的解法还会更新的。
这种题目所幸的是一般n都会给的很小。就几乎是明摆着告诉你要暴力。若果题目给的n很大的话。建议从打表或者找规律那方面考虑。
题目链接：https://vjudge.net/problem/UVA-440
AC代码：
#include <bits/stdc++.h> using namespace std; int y(int n,int m) { int s = 1, i; for (int i = 2; i <= n-1; i++) s = (s + m - 1) % i +1; return s+1; } int main() { int m, n; while (cin >> n && n) { for (m = 1; ; m++) if (y(n,m) == 2) break; cout << m << endl; } return 0; }
约瑟夫环变形问题六：
一圈共有N个人，从第一个人开始报数，每轮报到M的人，之前报1,2,3,4···，m-1的人出局，保证n-1为m-1的倍数，求最后出局的人的位置
解题思路：
参考了https://blog.csdn.net/ArkhamOrginal/article/details/52925997
很抱歉没找到这道题的oj或者说我进不去。（qAq)
这里给出题面：
【题目描述】
YJC 很喜欢玩游戏，今天他决定和朋友们玩约瑟夫游戏。
约瑟夫游戏的规则是这样的：n个人围成一圈，从1 号开始依次报数，当报到m 时，报1、2、…、m-1 的人出局，下一个人接着从1 开始报，保证(n-1)是(m-1)的倍数。最后剩的一个人获胜。
YJC 很想赢得游戏，但他太笨了，他想让你帮他算出自己应该站在哪个位置上。
【输入格式】
第一行包含两个整数n 和m，表示人数与数出的人数。
【输出格式】
输出一行，包含一个整数，表示站在几号位置上能获得胜利。
【输入样例】
1
10 10
【输出样例】
1
10
【数据范围】
1
对于30%的数据，2 ≤ n ≤ 1000。
对于70%的数据，2 ≤ n ≤ 1000000。
对于100%的数据，2 ≤ m ≤ n ≤ 2^63-1
这道题感觉跟原来的约瑟夫环完全不一样了。首先我们可以将
推公式找规律。问什么设什么，设置一个函数solve（n),表示在这n个人中进行约瑟夫游戏时最后一个人的编号。下面思考递归。
当前有n个人的话，那么这x个人可以分成两部分：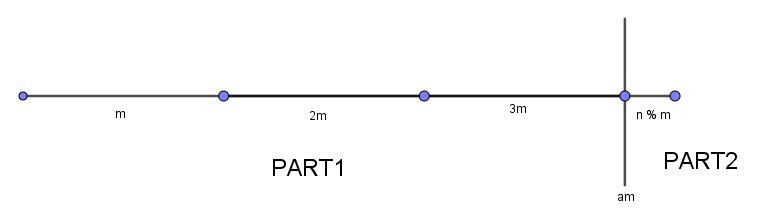
前面的一个部分可以被均分为了a组，每一组都有m个数；后面的一个Part有任意个，但是小于m。前面的Part1里面的人数显然是m的a倍，那么未出局的就是编号为m的整数倍的人；后面的Part2是不足再报m个数的人，总共数量是n%m。
我们继续对这些剩下的人重新编号（因为还有人没有报数，所以新的编号要从当前编号为am+1的人开始），将后面的n%m个人拉到新队伍的前面来。而前面总共是n/m组，那么此时还未出局的总人数为Part1的n/m个人和Part2的n%m个人。我们继续在这些人里重新进行约瑟夫游戏。
什么时候停止呢？显然最后肯定会有一个人留下来（n-1是m-1的整数倍），所以边界是solve(1)=1。
此时递归已经开始回溯，返回值是这一轮进行以后留下来的人的标号。我们要求出他在上一轮进行后留下来的编号，只需要找到他的位置即可。当前来说，因为后面的人数都小于m，那么也就是说这些人会全部出局（留下来的人在Part1），而且一定是m的整数倍（非整数倍都出局了）。设返回值为y，则我们可以知道他的编号为：(y-n%m)*m。
下面给出代码：
#include <bits/stdc++.h> #define maxn 1000005 using namespace std; long long n,m; long long f[maxn]; long long solve(long long x) { if(x==1) return 1; return m*(solve(x/m+x%m)-x%m); } int main() { cin >> n >> m; cout << solve(n); return 0; }
约瑟夫环变形问题七：
一圈共有2*k个人，从第一个人开始报数，每轮报到M的人出局，前k个是好人，后k个是坏人，求最小M使得坏人全部出局前好人没有一个出局。
题目链接：https://vjudge.net/problem/HDU-1443
解题思路：因为每次出去的人在每轮的编号都会大于k所以我们只要枚举m，之后check每次的编号是否小于等于了k就好了。
AC代码：
#include <bits/stdc++.h> using namespace std; int k,a[15]; bool IsGood(int x, int k){ int start = 0, n = k*2; while (n > k){ start = (start + x - 1) % n; //这里判断start是否大于k即可 if(start < k) return false; else n--; } return true; } void init(){ for (int i = 1; i <= 13; i++) for (int j = k; ; j++) if (IsGood(j, i)) {a[i] = j; break;} } int main(){ ios::sync_with_stdio(0); cin.tie(0); init(); while(cin >> k){ if (!k) break; cout << a[k] << endl; } return 0; }
约瑟夫变形问题八：
一共有n个人，每次报到m的人出去，问第k次出去的人的位置
#include<bits/stdc++.h> using namespace std; typedef long long ll; int t; ll n,m,k; int main(){ scanf("%d",&t); int kase = 0; while(t--){ scanf("%lld%lld%lld",&n,&m,&k); ll ans = 0; if(k >= m){ for(int i=1;i<=m;i++) ans = (ans+k-1)%(i+n-m)+1; } else{ if(k==1){//k=1的时候需要特判 ans = m; printf("Case #%d: %lld\n",++kase,ans); continue; } ll tt = 1; ll r = 0; ans = (ans+k-1)%(1+n-m)+1; while(tt<m){ r = (tt+n-m-ans+k-2)/(k-1);//向上取整即可 if(m-tt<r)r = m-tt;//如果溢出取最后一个 if(r==0)r++;//注意如果为0要++，否则会进入死循环 tt+=r;//更新最新的人数 ans = (ans+k*r-1)%(tt+n-m)+1; } } printf("Case #%d: %lld\n",++kase,ans); } return 0; }
希望大家能喜欢我的博客鸭~
