斯坦纳树学习笔记

斯坦纳树

前置

• 【百度一下】
• 会用到的知识：状压DP，spfa（或者一些最短路算法），生成树基础知识。

问题引入：

• 假如有$n$个城市，计划修一些道路，每条路有一些花费（花费均为正），现在请你求出使得$n$个城市连通的最小花费。

我们可以知道使这$n$个城市连通所选的边尽量越少越好，那么显然我们至少需要$n-1$条边，那么则就是一个树，于是我们可以使用最小生成树算法（Prim或者Kruskal）轻松解决这个问题。

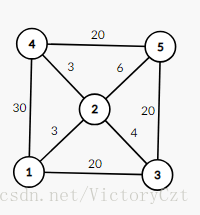
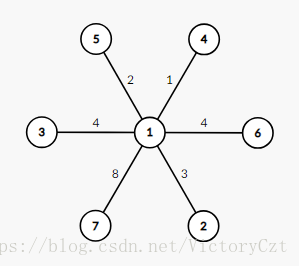
那么如果现在有一些中转点，可以让一些道路在这里中转，也就是这些点不一定用，但是用了有可能使得修路的花费更少，如下图：

我们假如点号为$1,3,4,5$的点为城市，$2$号点为中转站。
如果我们仍然只用$1,3,4,5$号点，那么道路的花费则为$90$
但是我们使用中转站$2$号点，那么代价大大减小，为$16$
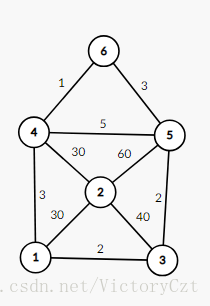
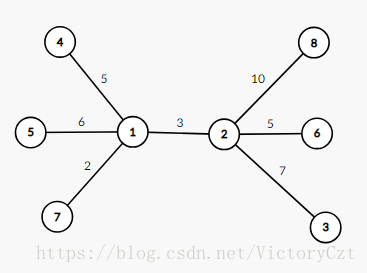
但是如果所有的点都选，如下图，也就不一定优秀了。

此时$6$号点也是中转站，$1,3,4,5$还是城市，$2$号点还是中转站，选择点$1,3,4,5,6$是最优的，为$11$。
所以这时，最小生成树就不能解决我们的问题了。

---

当一般所需要连通点集比较小（我们把必须要连通的点称作必须点），那么我们可以用一个动态规划（DP）来求的最优解。

点集比较小，大多数情况下可以状压，用二进制位的$0/1$来表示当前这个必须点是否已经连通。

暴力的想就是状压所有的点，就令$f[S]$表示当前连通集合状态为$S$，然后$2^n$枚举集合与和$n^2$的枚举新加的点和连边转移，这样总的复杂度为$n^22^n$（$n^2$是不会满的），且空间为$2^n$，似乎复杂度不是很优秀。

我们继续观察，发现有很多不需要的状态（也就是没有必须点的状态），所以我们可以这样转化一下状态的描述，$f[i][S]$表示当前的连通块的根为$i$，必须点的连通状态为$S$，所以我们要先对必须点重新编一个号，假如$k$个必须点，然后就从$0\sim k$编号，这时，$S$的状态只包含了必须点，那么就会去掉很多不必要的点，但是有些不必要的点可能还是会选，所以我们再加上一维$i$，表示当前的根，这样就可以描述所有有效状态了。

下面我们来看转移，分为两种：

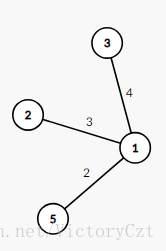
1. 按照点为媒介进行连通块的合并，也就是如下图这样，假如$1,2,3,4$为必须点：
   
   $f[1][1110]$状态
   
   $f[1][1001]$状态

合并的图如下图：

这两个可以合并为$f[1][1111]$状态，转移如下：
$f[1][(1110)|(1001)]=min(f[1][(1110)|(1001)],f[1][1110]+f[1][1001]) \\ f[1][1111]=9+13=21$
如果有点权的话，转移会把根节点多算一次，所以减去，下面$val[i]$表示$i$号点的点权，就为：
$f[1][(1110)|(1001)]=min(f[1][(1110)|(1001)],f[1][1110]+f[1][1001]-val[1])$

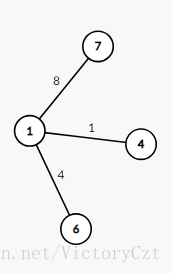
2. 按照边为媒介转移，也就是如下图这样，假如$1,2,3,4$为必须点：

其实这是两个集合，分别为$f[1][1001]$和$f[2][0110]$，但是我们可以通过这个边$1\rightarrow 2$将它们连接起来，那么转移如下，我们将它转移为$1$为根的：

$f[1][(1001)|(0110)]=min(f[1][(1001)|(0110)],f[1][1001]+f[2][0110]+side[1][2]) \\ side[1][2]=3$

所以这样就可以转移所有的状态了。

---

代码实现

对于第一种转移，我们枚举集合和子集还有根节点进行转移，复杂度为$n3^k$，其中$k$为必须点的个数（当$k=n$时，我们就可以使用最小生成树算法）。

然后边的怎么办呢？总不能$O(m)$的枚举边（假设边有$m$条），然后$(2^k)^2$枚举边两边的情况吧，这样的复杂度为$O(m(2^k)^2+n3^k)$，$m$最大会达到$\frac{n\times (n-1)}{2}$条，所以不能这样暴力转移。

那么我们可以想，对于图上的边权和最小，我们可以使用最短路之类的算法啊，这里介绍$\rm SPFA$。

我们可以通过像跑分层最短路一样，确定一个状态$x$，然后将所有的可以去更新答案的$f[i][x]$加入队列，然后开始进行$\rm SPFA$，每次枚举一条边和一个点，假如当前点为$a$，枚举的边对面的点为$v$，则可以更新的话就$f[v][x|(id[v])]=f[a][x]+side[a][v]$，$id[v]$为$v$的二进制编号，如果为不必须点，则为0，如果有点权的话就为$f[v][x|(id[v])]=f[a][x]+side[a][v]+val[v]$，这样用一个集合加一条边和一个点的更新（松弛操作）方式，也就相当于完成了我们的第二种转移。

此时在一般的图上，$\rm SPFA$一次的均摊复杂度为$O(n\times t)$，近似看作$O(n)$，（$t$一般小于$3$左右，但是特殊构造的图，如稠密图就可能比较大，但是不会超过$m$（边数）），所以用边更新的复杂度为$n2^k$，所以总复杂度就为$O(n2^k+n3^k)$，大概能在$1s$跑过$k\leq 10,n\leq 300,m\leq 10000$的数据吧。

在所有的点权边权均为正数的情况下，则可以使用$\rm Dijistra+$堆优化，可以将复杂度保证为$O(nlogn2^k)$，而不是$\rm SPFA$的$O(n\cdot t2^k)$

下面给出我的模板题目的代码，【模板题in洛谷】

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define RG register
using namespace std;
const int M=3e5+10;
const int S=1<<10|1,N=510;
const int inf=0x3f3f3f3f;
inline char nc(){
    static char buf[100000],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
void readInt(int &x){
	 x=0;RG char c=0;
	 while(c<'0'||c>'9')c=nc();
     while(c>='0'&&c<='9'){x=x*10+(c&15);c=nc();}
}//快读fread，读入请用文件读入
int f[N][S],id[N],sze,ans;
int que[M],p,q;bool vis[N],isimp[N];
struct ss{
	int to,last,w;
	ss(){}
	ss(int a,int b,int c):to(a),last(b),w(c){}
}g[M<<1];
int head[N],cnt;
void add(int a,int b,int c){
	g[++cnt]=ss(b,head[a],c);head[a]=cnt;
	g[++cnt]=ss(a,head[b],c);head[b]=cnt;
}
void init(){
	sze=0;ans=inf;
	memset(f,-1,sizeof(f));
}
int n,m,useful,val[N],ned[N];
void spfa(int x){
	for(;p<=q;p++){
		int a=que[p];
		vis[a]=0;
		for(RG int i=head[a];i;i=g[i].last){
			int v=g[i].to,y=(id[v]|x);
			if(f[v][y]==-1||f[v][y]>f[a][x]+g[i].w+val[v]){
				f[v][y]=f[a][x]+g[i].w+val[v];//媒介为边的更新
				if(y==x&&!vis[v]){
					vis[v]=1;que[++q]=v;
				}
			}
		}
	}
}
int staner(){
	init();
//	for(int i=1;i<=n;i++)if(ned[i])f[i][id[i]=(1<<sze)]=0,++sze;
	for(int i=1;i<=useful;i++)f[ned[i]][id[ned[i]]=(1<<(i-1))]=val[ned[i]],isimp[ned[i]]=1;//重新编号
	for(int i=1;i<=n;i++)if(!isimp[i])f[i][0]=val[i];//初始值为点权
	sze=useful;
	int up=(1<<sze);
	for(RG int x=1;x<up;++x){
		p=1;q=0;
		for(RG int i=1;i<=n;++i){
			if(id[i]&&(!(id[i]&x))) continue;
			for(RG int y=(x-1)&x;y;y=(y-1)&x){
				int xx=id[i]|y,yy=id[i]|(x-y);
				if(f[i][xx]!=-1&&f[i][yy]!=-1){
					if(f[i][x]==-1||f[i][xx]+f[i][yy]-val[i]<f[i][x]){
						f[i][x]=f[i][xx]+f[i][yy]-val[i];//媒介为点，更新
					}
				}
			}
			if(f[i][x]!=-1)que[++q]=i,vis[i]=1;//加入队列
		}
		spfa(x);//用spfa，边去松弛更新
	}
	--up;
	for(int i=1;i<=n;i++)if(f[i][up]!=-1&&f[i][up]<ans)ans=f[i][up];
	return ans;
}
int a,b,c;
int fa[N];
int find(int a){return fa[a]==a?a:fa[a]=find(fa[a]);}
struct edge{
	int u,v,w;
	edge(){}
	edge(int a,int b,int c):u(a),v(b),w(c){}
	void in(){readInt(u);readInt(v);readInt(w);}
	bool operator <(const edge &a)const{return w<a.w;}
}e[M];
int mst(){
	int tot=0,ans=0;
	sort(e+1,e+m+1);
	for(RG int i=1;i<=n;++i)fa[i]=i;
	for(RG int i=1;i<=m;++i){
		int a=find(e[i].u),b=find(e[i].v);
		if(a==b) continue;
		fa[a]=b;
		ans+=e[i].w;
		if(++tot==n-1) break;
	}
	return ans;
}
int main(){
	readInt(n);readInt(m);readInt(useful);
	for(int i=1;i<=n;i++)readInt(val[i]);
	for(int i=1;i<=useful;i++)readInt(ned[i]);
	if(useful>10){
		//最小生成树的部分分
		int sum=0;
		for(RG int i=1;i<=n;++i)sum+=val[i];
		for(RG int i=1;i<=m;++i)e[i].in();
		cout<<mst()+sum<<'\n';
		return 0;
	}
	for(RG int i=1;i<=m;++i){
		readInt(a);readInt(b);readInt(c);
		add(a,b,c);
	}
	cout<<staner()<<'\n';
	return 0;
}