LOJ535「LibreOJ Round #6」花火-题解

题目地址【IN-Loj】

记得开long long,空间要两倍！

---

• 题目简述

给你一个$n$的全排列，相邻的之间可以任意交换，只有一次可以交换不相邻的位置的数的机会，求出能让其排好序的最少交换次数。

---

分析：

如果没有那一次不相邻的交换机会，那么就是一个求逆序对个数的裸题了。

那么有了这个之后，我们暴力的想法是枚举$n^2$的交换情况，每次再$nlogn$计算逆序对个数，总复杂度为$n^3logn$，但是显然过不了。

所以我们考虑，对于一个点，我们可以看作这样的一个点对$(i,h_i)$，表示下标为$i$，高度为$h_i$，那么我们交换的点必须要满足：$i<j,h_i>h_j$，否则会增加逆序对的个数。

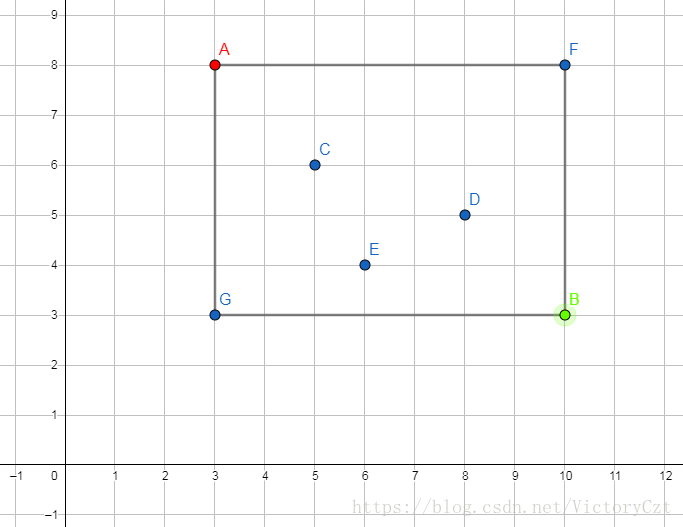
而我们将其放在平面上来看，会是这样的:

红色的点为$(i,h_i)$，绿色的点为$(j,h_j)$，那么如果交换这两个点，我们可以发现，减少的逆序对个数为$1+\text{矩形内的点的个数}$，因为你原来矩形内的每个点和点$j$会产生逆序对，然后矩形内的点和点$i$产生逆序对，最后点$i,j$的逆序对，所以交换后就会减少这么多。

那么我们只需找到包含点最多的矩形，然后将其左上角的点和右下角的点交换之后答案就为：

$ans=tot-\text{矩形内的点的个数}\times 2 -1+1$

$tot$为总的逆序对个数，后面$-1+1$是因为开始$i,j$会减少一个，但是你交换$i,j$又会增加一步操作，所以是这样。

---

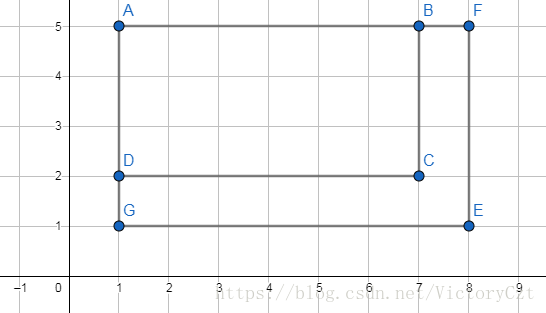
我们暴力找的话还是$n^2$的，但是我们可以发现，对于一个点$(k,h_k)$，如果$k<i,h_k>h_i$，那么用点$k,j$肯定比点$i,j$要优秀，因为这两个矩形是包含的关系，如下图：

图上点$C$为点$k$，$A$为点$i$，$B$为点$j$。

同理,对于一个点$(w,h_w)$，如果$w>j,h_w<h_j$，那么$i,w$肯定比$i,j$要优秀，如下图：

点$A$为点$i$，点$C$为点$j$，点$E$为点$w$。

---

所以根据这个单调性，我们可以用整体二分+主席树找到包含点最多的矩形，具体细节参考下面这个博客【Orz-IN】

但是，这个方法是$O(nlog^2n)$的，所以虽然能过，但是常数巨大且不好写。

---

不妨反过来思考。
我们可以对于每一个点，找出包含它的最大的矩形。
那么我们对于点$(i,h_i)$，我们前面找最小的$l$，且满足$l<i,h_l<h_i$，找后面最大的$r$，且满足$r>i,h_r<h_i$，这个就是能包含它的最大的矩形了，所以对于所有点$(j,h_j)$，只要满足$l\leq j\leq r,h_r\leq h_j\leq h_l$，那么这个点就会对其作出贡献。

我们对于矩形不好处理，所以将其转化为点对，一个点$(x,y)$表示左上角的下标在$x$右下角的下标在$y$的矩形，那么我们每次只用在$(l\sim i-1,i+1\sim r)$内的点加$1$即可。

所以我们用扫描线的思想将一个矩形拆成两条线，一条入线，一条出线。
我们按照新的平面的$y$坐标从下往上扫，所以我们将原来一个$(i,h_i)$点表示的矩形拆为$(l\sim i-1,i+1)$的一条线和$(l\sim i-1,r+1)$的两条线，当我们遇到第一条线时表示进入了这个矩形，就将$l\sim i-1$加$1$，遇到第二条线就表示已经出了这个矩形，我们要将这个矩形的影响消除，就将$l\sim i-1$减$1$，然后我们每次取当前这条线上的最大值更新最多点矩阵的点数即可，这个可以用一个线段树维护。

所以先预处理，用归并排序或者树状数组的方式求出总的逆序对的个数$tot$，记最多的点数为$p$，答案就为:
$tot-2\times p$

所以在$nlogn$的预处理，$nlogn$的求$p$，$O(1)$回答答案即可。
总复杂度$O(nlogn)$，比分治的$O(nlog^2n)$要优秀的多。

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int M=3e5+10;
int n,H[M];
int lmax[M],rmin[M];
struct node{
	int l,r,type,ck;
	node(){}
	node(int a,int b,int c,int d):l(a),r(b),type(c),ck(d){}
	bool operator <(const node &a)const{return ck<a.ck||(ck==a.ck&&type>a.type);}
}line[M<<1];//因为每个矩形拆成两条线，所以空间开两倍
int tot;
int maxv[M<<2],lazy[M<<2];
void pushup(int o){
	maxv[o]=max(maxv[o<<1],maxv[o<<1|1]);
}
void pushdown(int o){
	if(!lazy[o]) return;
	maxv[o<<1]+=lazy[o];
	maxv[o<<1|1]+=lazy[o];
	lazy[o<<1]+=lazy[o];
	lazy[o<<1|1]+=lazy[o];
	lazy[o]=0;
}
void update(int o,int l,int r,int L,int R,int v){
	if(L<=l&&r<=R){
		maxv[o]+=v;lazy[o]+=v;
		return;
	}
	int mid=l+r>>1;
	pushdown(o);
	if(L<=mid) update(o<<1,l,mid,L,R,v);
	if(R>mid) update(o<<1|1,mid+1,r,L,R,v);
	pushup(o);
}
//线段树区间加维护最大值
#define lowbit(a) ((a)&(-(a)))
ll bit[M];
void add(int a,ll b){
	for(;a<=n;a+=lowbit(a))bit[a]+=b;
}
ll query(int a){
 	int ans=0;
	for(;a;a-=lowbit(a))ans+=bit[a];
	return ans;	
}
//树状数组求逆序对个数
ll ans;//记得开long long
void init(){
	for(int i=n;i>=1;i--){
		ans+=1ll*query(H[i]);
		add(H[i],1);
	}	rmin[n+1]=n+1;
	for(int i=1;i<=n;i++)lmax[i]=max(lmax[i-1],H[i]);
	for(int i=n;i>=1;i--)rmin[i]=min(rmin[i+1],H[i]);
	//求取前缀最大和后缀最小
	int l,r;
	for(int i=1;i<=n;i++){
	//查询l,r，并加入扫描线
		l=lower_bound(lmax+1,lmax+n+1,H[i])-lmax;
		r=lower_bound(rmin+1,rmin+n+1,H[i])-rmin;
		if(rmin[r]>H[i])--r;
		if(l>=i||r<=i)continue;//排除不合法的情况
		line[++tot]=node(l,i-1,1,i+1);
		line[++tot]=node(l,i-1,-1,r+1);
	}
	sort(line+1,line+tot+1);//按照y排序
}
ll maxdel;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d",&H[i]);
	init();
	for(int i=1;i<=tot;i++){
		update(1,1,n,line[i].l,line[i].r,line[i].type);
		if(maxv[1]>maxdel)maxdel=maxv[1];//更新找最大
	}
	printf("%lld\n",ans-2ll*maxdel);//输出答案
	return 0; 
} 

类似题目【IN】