牛客网比赛216C-小K的疑惑-题解

题目地址【IN】

写了一遍就过了，ヾ(◍°∇°◍)ﾉﾞ凯森

题意简述

给你一棵$n$个节点的树，每条边有边权，定义$dis(i,j)$为点$i$到$j$的距离模$2$后的值，问你有多少个三元组$(i,j,k)$满足$1\leq i,j,k\leq n$且$dis(i,j)=dis(j,k)=dis(i,k)$。

数据范围$n\leq 1e4,0\leq val\leq 233$

---

我们可以发现$(a+b)\%2=(a\%2\ xor\ b\%2)$

那么$dis(i,j)$就变成了$i\rightarrow j$的路径权值异或和。

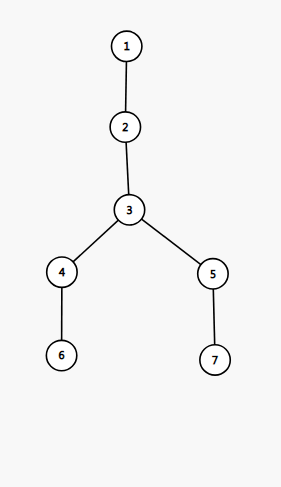
那么，由于$a\ xor\ a=0$，异或是可以相消的，所以我们可以$dfs$处理一个数组$d[i]$，表示节点$i$到根（这里默认根为$1$号点）的路径上的异或和，那么$dis(i,j)=d[i]\ xor\ d[j]$，原因如下图：

$6\rightarrow 1$的路径上有$1-2,2-3,3-4,4-6$

$7\rightarrow 1$的路径上有$1-2,2-3,3-5,5-7$

那么将$d[6]\ xor\ d[7]$，其中重复的边$1-2,2-3$就会被异或掉，然后剩下的就变成了$6-4,4-3,3-5,5-7=dis(6,7)$了。

所以$dis(i,j)=d[i]\ xor\ d[j]$

那么由于只有$d[i]=d[j]=d[k]$的时候才会成为一个合法的三元组，而$d[i]$的值只有$0,1$，所以统计一下个数，我们令$cnt_0,cnt_1$分别为$0,1$的个数，那么答案就为$(cnt_0)^3+(cnt_1)^3$（由于$i,j,k$可以交换顺序，所以方案数为个数的三次方）。

代码非常简单：

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int M=1e5+10;

struct ss{
	int to,last,len;
	ss(){}
	ss(int a,int b,int c):to(a),last(b),len(c){}
}g[M<<1];
int head[M],cnt;
void add(int a,int b,int c){
	g[++cnt]=ss(b,head[a],c&1);head[a]=cnt;
	g[++cnt]=ss(a,head[b],c&1);head[b]=cnt;
}
ll rec[2];
void dfs(int a,int b,int val){
	++rec[val];
	for(int i=head[a];i;i=g[i].last){
		if(g[i].to==b) continue;
		dfs(g[i].to,a,val^g[i].len);
	}
}
ll cude(ll a){return a*a*a;}
int a,b,c,n;
int main(){
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
	}
	dfs(1,0,0);
	printf("%lld\n",cude(rec[0])+cude(rec[1]));
	return 0;
}