ENGG1310 P3.2 Resistor, Inductor, Capacitor, and RLC Circuits
这一节里关于三相电的内容最为重要,注意复习
Resistor 电阻
Physical 2-terminal energy-dissipative device.
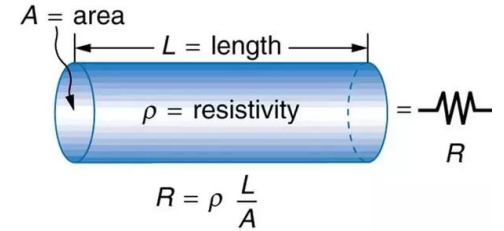
电阻定律
电阻同样与温度 有关 (然而 Temperature is neglected for the time being),一般来说温度越高,电阻越大
电阻的伏安性质
电阻的 功率损失 (Power Loss) (即电能损失的功率/热能产生的功率)
导体的电阻 (resistance of a conductor)
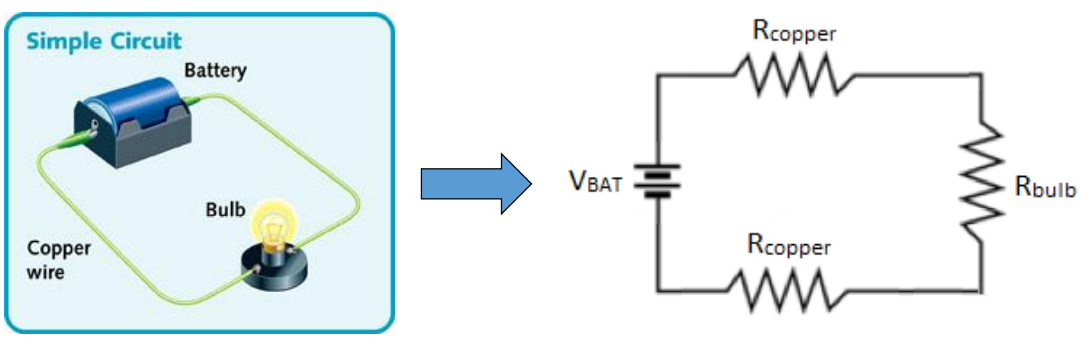
导体/负载 (conductors/loads) 的电阻 (resistance) 常以一个物理电阻 (physical resistor) 代表
Resistor Rating
电阻通常标识其最大功率 (rated in Watts)
电阻的功率不会超过该最大功率
Resistor Type
电阻上通常会有许多颜色带 (colour bar) 来标识其电阻
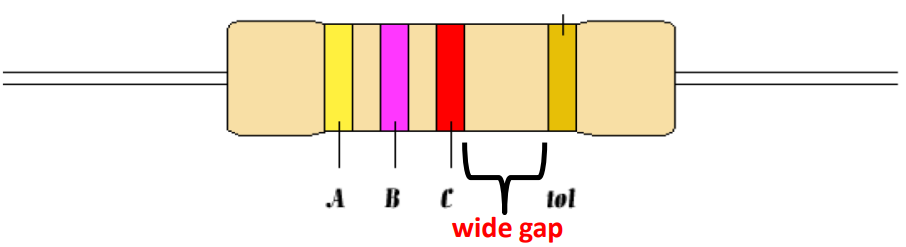
(具体的颜色-数字对应关系查看 Slides)
Variable Resistor/Rheostat 可变电阻(滑动变阻器)

电路的类型
Series, Parallel and Mixed
- Series circuits 串联电路 (connected end-to-end)
- Parallel circuits 并联电路 (both ends are connected)
- A mixture of both 混联电路
基尔霍夫电压/电流定律 Kirchhoff's Law
- Kirchhoff’s Voltage Law (KVL)
在任意电路闭环中 (closed loop),总电势差 (potential drop) 总电动势 (EMF, Electromotive force)
很好理解,电动势的产生使得电势升高,又在随后被降低至原位 (本质上是能量守恒定律) - Kirchhoff's Current Law (KCL)
对于电路中的任意节点 (node/junction),流入该节点的电流 流出该节点的电流
流入节点的电流为 ,流出节点的电流为 ,所以对于某个节点 ,
Delta-Star Transformation (- transformation)
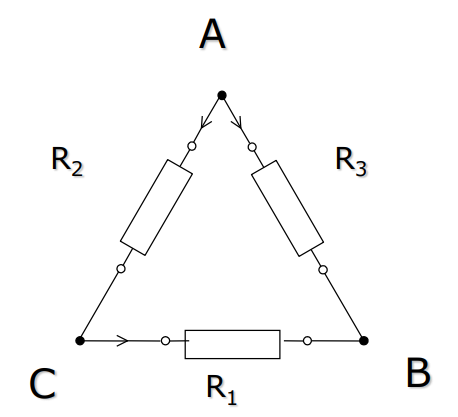 [ 型电路]
[ 型电路]
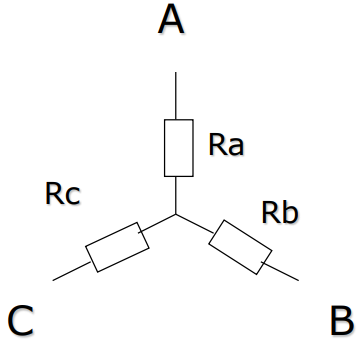 [星型 / 型电路]
[星型 / 型电路]
观察 型电路,我们利用并联电阻法则计算两点之间的等价电阻
若要将 型电路转变为 型电路,有
三个方程,三个位置数,我们解得
( 是 邻接的电阻)
( 是 邻接的电阻)
( 是 邻接的电阻)
In general form,即是 ( 是 邻接的电阻)
Potential Divider Circuit 串联分压
对于串联的两电阻 ,流过他们的电流
因此有
若总电动势为 ,则 ,
Current Divider Circuit 并联分流
对于并联的两电阻 ,其上施加的电压
因此有
若流过 的总电流为 , 则
Series Connection of Cells 串联单体
Cell 指的是电池的单体,每一个 Cell 都能提供 的电动势
个 Cells 进行串联,得到的电动势为
注意极性:串联时,一个单体的正极连接另一个单体的负极
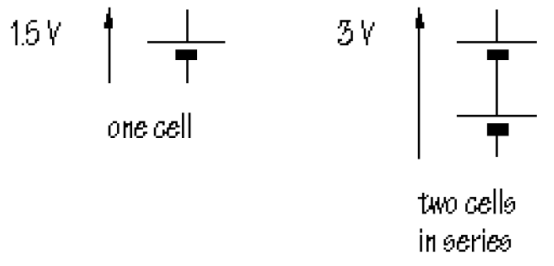
Parallel Connection of Cells 并联单体
并联的 Cell 虽然提供的电动势相同,但是产生的电流更大
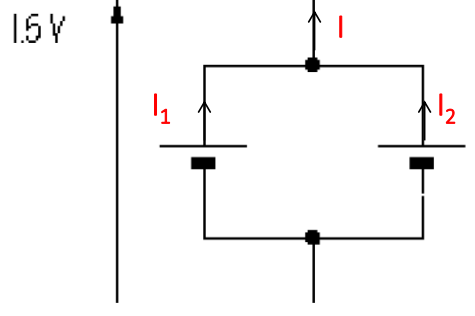
理想情况 (Cell 的电阻不计) 下,两个 Cells 向负载提供相同的电流
三相交流电 Three-Phase AC
交流电 (Alternating Current) 的产生,使得远距离输电成为可能
(由于交流电的电流不断的变化,其引发的电磁感应现象使得电压的变化相对容易)
AC Resistive Circuits
这是一个最简单的 AC 电路,由 AC power source 与电阻组成
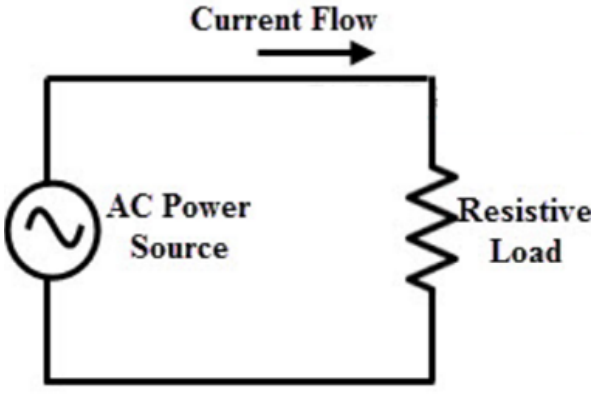
这是该电路的伏安性质:

- 电压与电流都是 Sinusoidal form,且频率相同
- 电压与电流 in phase with each other
- 在任意时刻,电压与电流都满足 Ohm's Law
Phase & Phasor
Phasor 相量
在工程学中,一个正弦函数 的 不随时间变化,那么该函数是一个 phasor (相量)
或者说,振幅,频率与相位角不随时间变化,从而保证了相位 (phase, ) 不随时间变化
两个 phasors 可以有相同的频率与振幅,但相位不同: 相位差 (phase difference) 即使两个相同频率的 phasors 之间相位之差
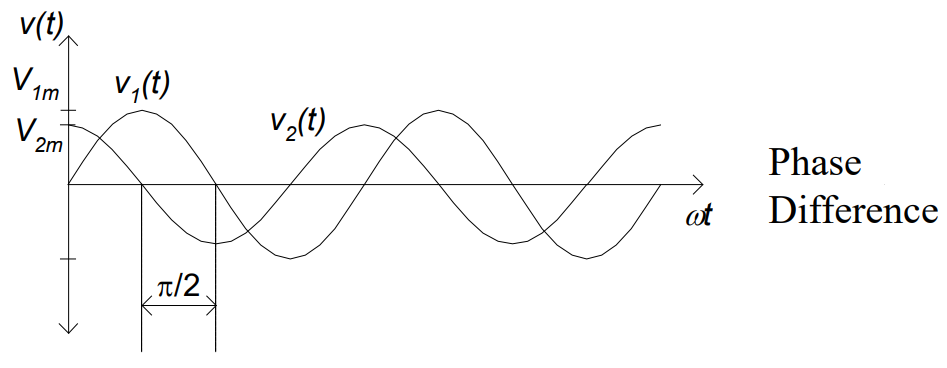
如上图,两个 phasors 的相位差 (phase difference)
3-Phase 三相
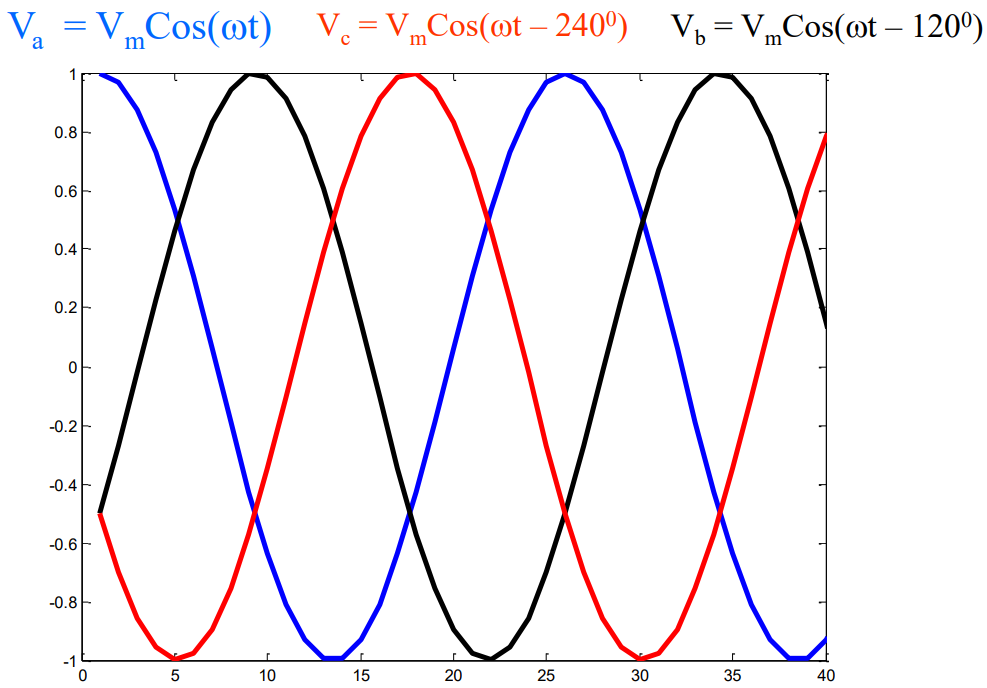
三相即为三个频率相同的 phasors: 这三个 phasors 两两之间的相位差相同 ()
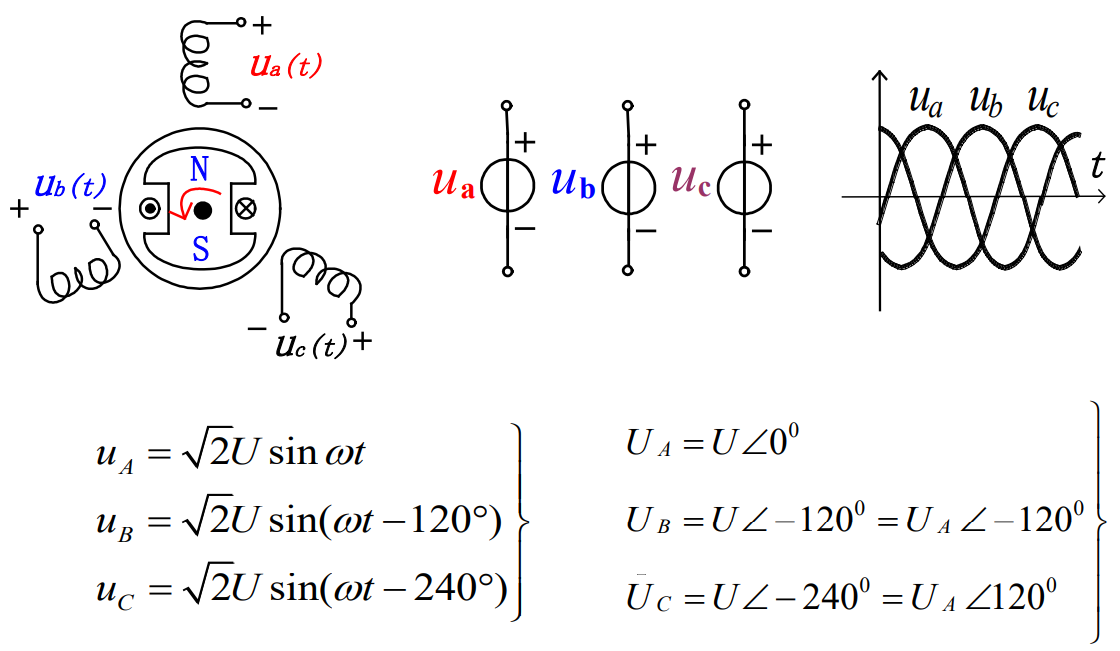
(上图是三相发电机的平衡系统)
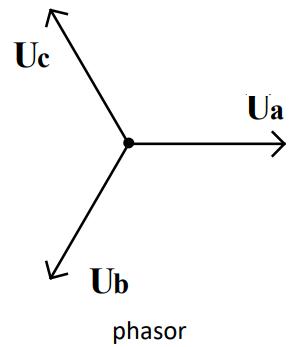
三相中三个 phasors 的关系: 可以看出,任意两个 phasors 之间的相位差都是
3-Phase Source & Load
三相电路有两种接法,就是我们之前所提到的 型接法与 星/ 型接法
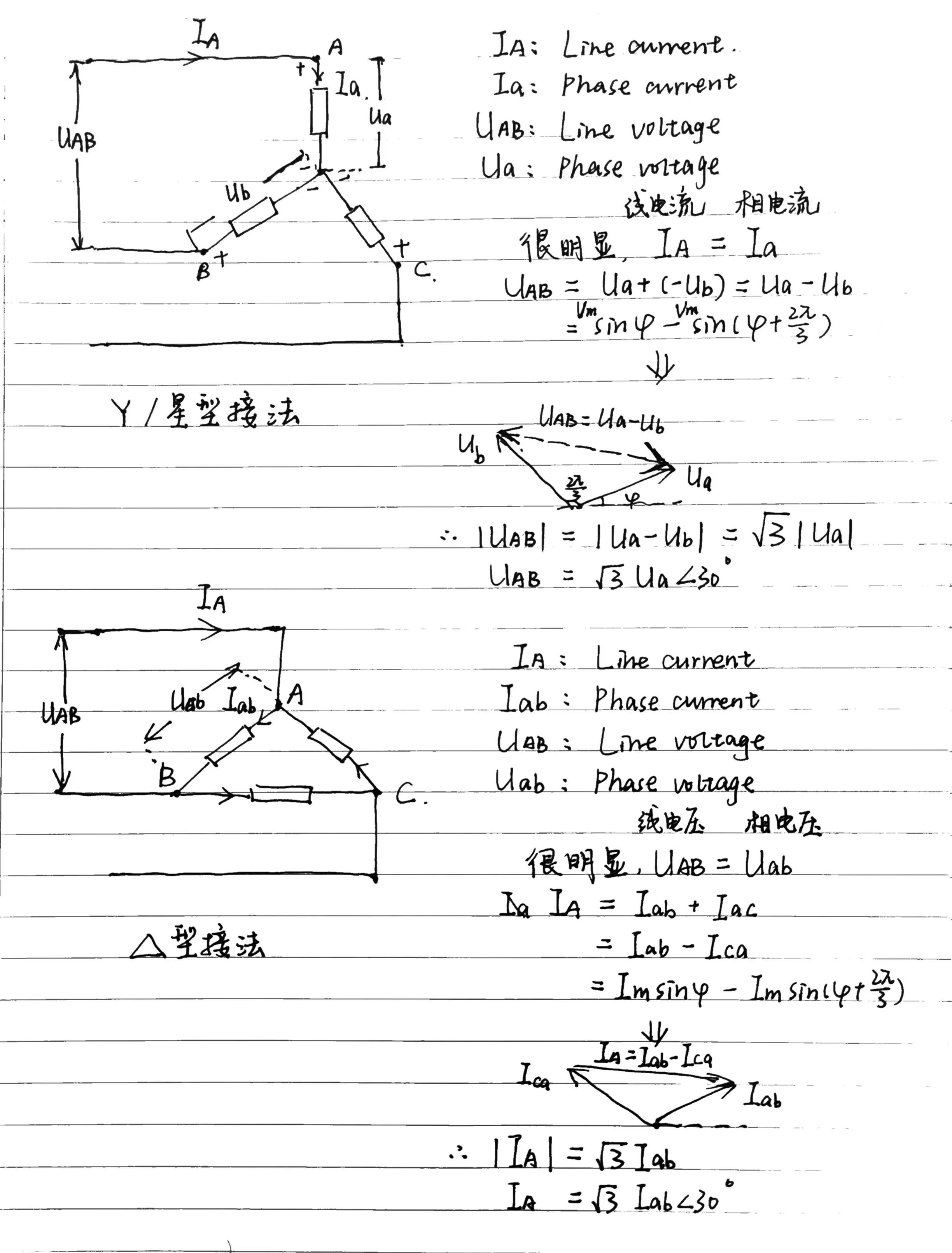
其中, 型接法 Line Current Phase Current, Line Voltage Phase Voltage
星/ 型接法 Line Current Phase Current, Line Voltage Phase Voltage
串/并联 AC resistive circuit
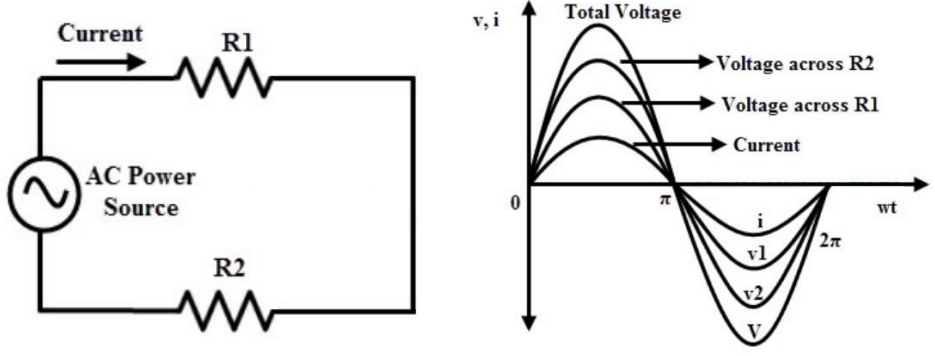
Series AC resistive circuit
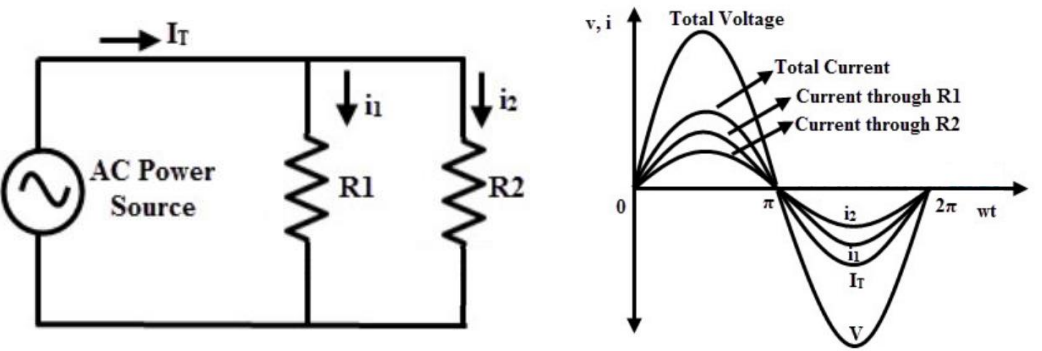
Parallel AC resistive circuit
很好理解,需要注意的是
- 电流时时刻刻与电压同步 (in phase with)
- 在涉及 AC 电路的计算时,电流与电压所采用的数值都是有效值 (RMS/effective value)
Capacitors 电容器
电容器是一种 2-terminal devices,通过两电极板储存能量 (以储存静电荷 electrostatic charges 的形式)。给定电压,电容器储存电荷的能力称为电容 (capacitance)
电容器的构成: parallel conductive plate seperated by dielectric insulating layer
电容的单位是 (Farad)
常见的单位还有
Polarised Capacitor 极性电容器
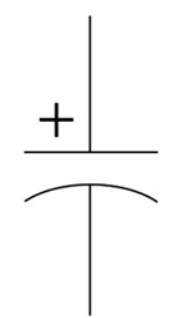
极性电容器的 极必须连接高电动势 (electromotive force) 端, 极连接低电动势端
因此,极性电容器大多用在 直流电路 (DC) 中
电容器的充电 charge 与放电 discharge
在 DC 电源下:
充电时,电容器两端电压 ,直到与电源电动势相等;电流则由最大值 直到
(这也是正/负电荷逐渐在导体板上积累的过程;充电完毕后,只要外部的电动势存在,电荷会一直留在导体板上)
放电时,电容器两端电压 ,直到变为 ; 电流由最大值 直到
电容 Capacitance
电容 (Capacitance) 用来定量描述电容器的储存电荷的性质:
外部施加的单位电压 (per unit voltage applied) 下,电容器能储存的电荷量 (the amount of charge)
即 或
其单位分别是: (电容), (电荷量,库伦), (伏特)
Energy Stored in Capacitor
当外部施加的电压为 时,电容为 的电容器能储存的电能
或
的单位是 (焦耳,Joules)
Capacitor value codes/label
电容器上通常有标识标注其电容
- 对大电容:电容直接打印在电容器上
- -digit code: 代表
- -digit code: 最后一个数字代表 的次方:
- -digit plus one letter code: 字母代表 tolerance
串联电容器 Capacitors in Series
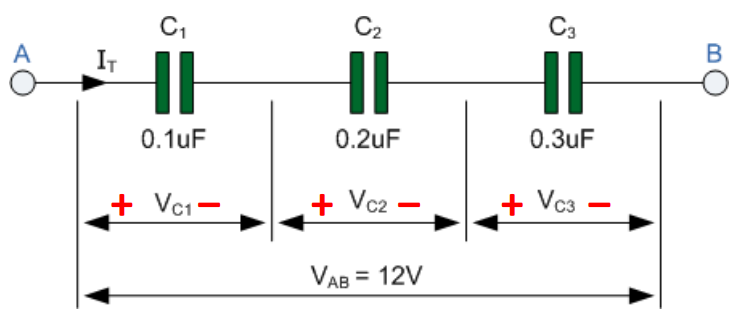
对于串联的电容器,电路中的电流时刻相等
且电容器所储存的电荷量也一定相等 (相邻电极板中,一方通过感应使另一方产生等量的异种电荷)
因为 ,又
有 ,于是
类似的, 个电容器串联,总电容的倒数与各电容的倒数有以下关系
并联电容器 Capacitors in Parallel
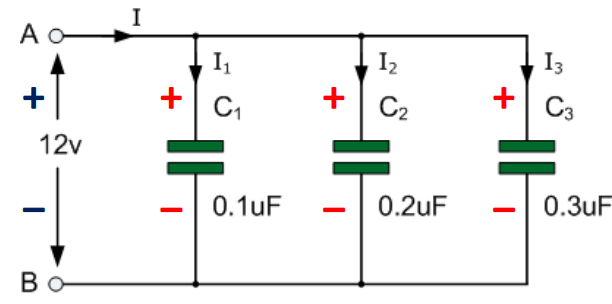
对于并联的电容器,每一条分支上的电压相等,即
类似的,对于 个并联的电容器,总电容
例题:
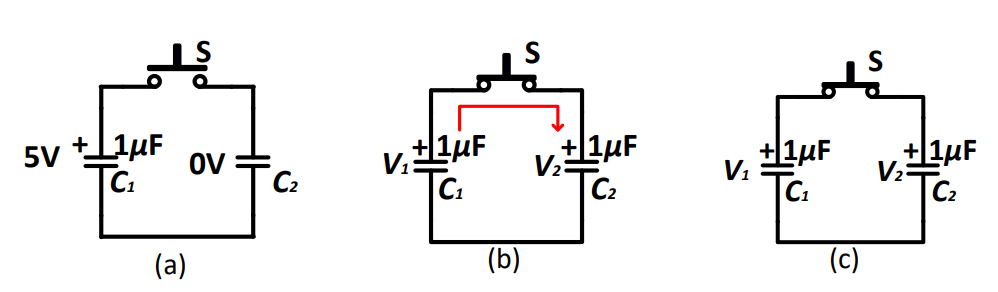
某电容器 向另一电容器 充电直至达到平衡状态
利用平衡状态下的电压关系 进行求解
Capacitors in AC circuits
- AC 的频率: 电容器高频通,低频断
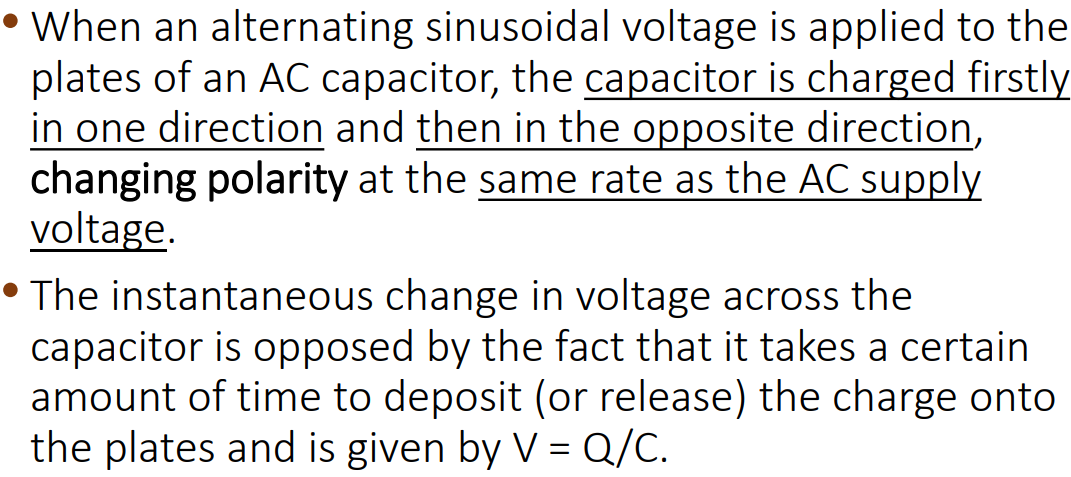
- 由于 AC 的方向持续改变,电容器也将会持续的进行充电/放电过程 (charging/discharging process),该过程导致了电压与电流的不同步 (out-of-phase)
电流将领先电压 个周期
Capacitors: Application
- 在电路中储存能量 ()
- Coupling (耦合) AC signal and Decoupling (解耦合) DC signal
- Smoothing and Filtering noise in signal
- 作为 LC 震荡 (tuned resonant) 电路 的组成部分
Inductors 电感器
电感器也是一种 -terminal device,其拥有的性质称为 电感 (inductance)
当电流流过电感器时,电感器以磁通量 (magnetic flux) 的形式储存能量
电感是由 central core 与紧紧缠绕其的导线组成的,central core 一般是一个 圆柱体 (cylindrical rod) 或是 环 (continuous ring)
电感的单位是 (Henry)
常见的单位还有
Energizing an inductor
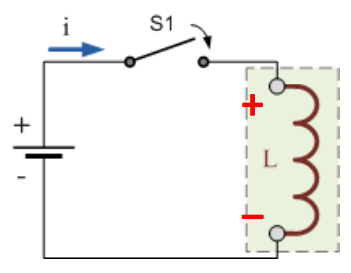
当直流电源连接电感器时,电流由小变大,直至打到 ( 为该电感器的电阻)
在此过程中,inductor magnetically energizes,将电流转化为磁场 (magnetic field)
Energy stored in inductor
与电容器类似,电感为 的电感器中储存的能量为
串联/并联 电感 Inductors in series/parallel

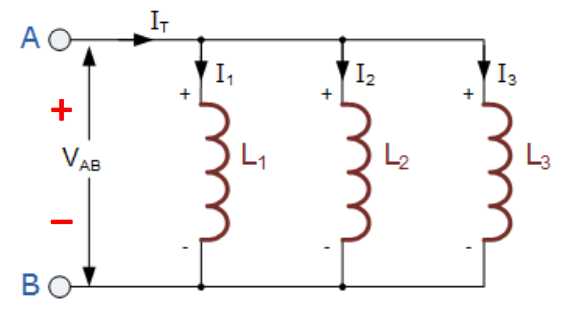
电感的计算公式不要求掌握,我们只需要记住总电感与各分电感的关系与电阻一致,即
- 在串联电感器系统中
- 在并联电感器系统中
Inductors in AC Circuits
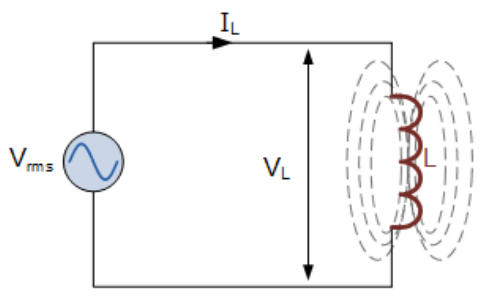
我们知道电压能够引致通过电感器的电流由 增长到最大值
而 AC 在电流增长到最大值之前 改变方向 (changes polarity),也就是说,电流相比电压是 延迟的 (delayed)
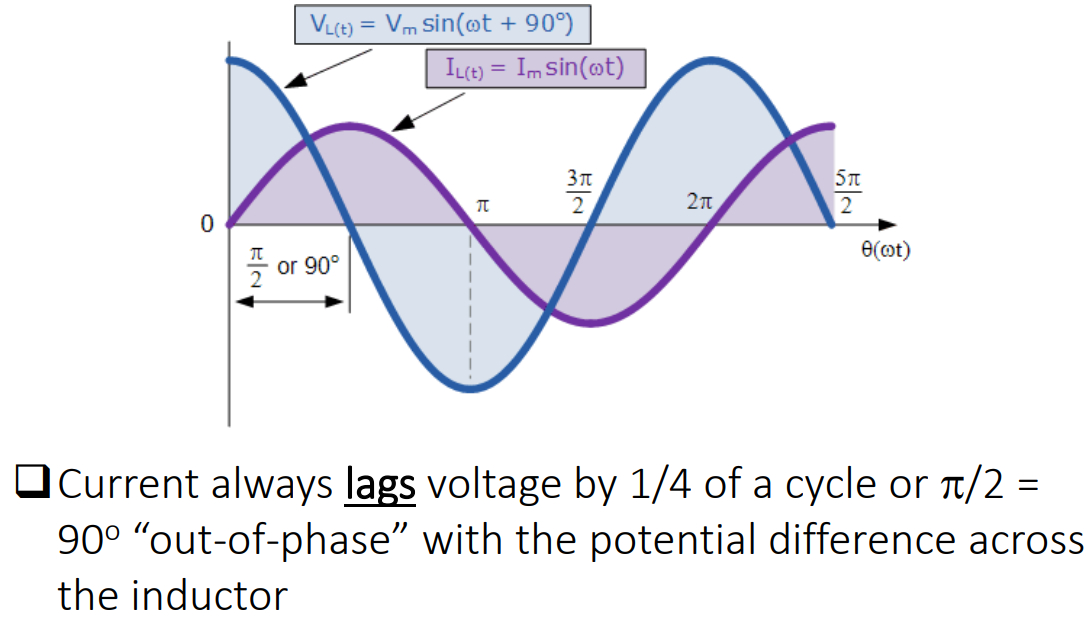
注意这一点!!-
- AC 电路中的电容器,电路中电流的相位 领先 (lead) 电容器两端电压相位
- AC 电路中的电感器,电路中电流的相位 落后 (lag) 电感器两端电压相位
Inductor Applications
- 在电路中储存能量
- As chokes to block AC signal and bypasses DC signal
- LC 震荡 (tuned resonant) 电路的组成部分
Reactance 电抗
电容器与电感器与电阻一样,都具有阻碍电流的作用
为了描述其阻碍电流的效果,我们定义容抗 , 感抗 (单位与电阻一致,为欧姆 )
例题
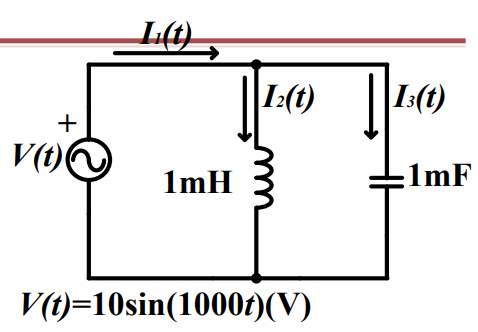
我们已知电压 ,求电流 ,则先计算电容和电感的 电抗 (reactance)
由 AC 电压的公式得 ,且
那么电流
(幅度: 电压/电抗电流;相位: 电流比电压领先 )
(幅度: 电压/电抗电流;相位: 电流比电压落后 )
代入对应得 即可求出瞬时电流




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
2022-04-06 Coursera 计算导论与 C 语言基础,北京大学
2022-04-06 Coursera Programming Languages, Part A 华盛顿大学 Week 4