COMP3357 Exercise

老师今天特意强调了考试，并且讲解了这些题，让人很难不怀疑......!!
在这里每道题都认真研究一下，做个记录

Group Theory

Quadratic residue

这个还比较好证，自己想出来了
首先，要证明某个集合是群，必须要证明它的 identity, inverse, closure, associativity 四个性质
identity: \(1=1^2=(-1)^2\pmod{p}\)，所以 \(QR_p\) 包含单位元 identity
inverse: 对于任意 \(a=x^2\pmod{p}\) 其逆元 \(a^{-1}=(x^{-1})^2\pmod{p}\)，所以 \(QR_p\) 包含逆元 inverse
closure: 对于任意两个集合中的元素 \(a=x^2\pmod{p}\) 与 \(b=y^2\pmod{p}\)，其乘积 \(ab=(xy)^2\pmod{p}\) 仍属于 \(QR_p\)，所以 closure 存在
associativity 继承自 \(Z_p^{*}\) ( \(QR_p\) 一定是 \(Z_p^{*}\) 的子集 )

对于任意 \(a\in QR_p\)，有 \(x^2=a\pmod{p}, \ x\in Z_p^{*}\)
一定存在 \((-x)^2=a\pmod{p}\)
且由于 \(p\) 是 \(>2\) 的质数，\((p-x)\neq x\)
则 \(Z_p^{*}\) 中的每一对 \((x, p-x)\) 对应 \(QR_p\) 中的一个 \(a\)
\(|QR_p|=|Z_p^*|/2=(p-1)/2\)

Perfect Secrecy

Exercise: Perfect Secrecy

复习一下完美加密的几个性质
\(\Pr[M=m|C=c]=\Pr[M=m]\)
\(\Pr[M=m_0|C=c]=\Pr[M=m_1|C=c]\) (这也是 perfect indistinguishability 的描述)

RSA

Adapted RSA with CRT

• (a)
  很明显，就不多赘述了
• (b)
  由于 \(g_1=g^{r_1(p-1)}\)
  有 \(g_1\equiv g^{r_1(p-1)}\pmod{p}\)，根据费马小定理，\(g_1\equiv 1\pmod{p}\)，即 \(g_1-1\equiv 0\pmod{p}\)
  所以 \(p|(g_1-1)\)
  我们计算 \(\gcd(g_1-1, N)\)
  • 若 \(\gcd(g_1-1, N)=p\)
    这样，我们成功的找到了 \(N\) 的 factorization，破解 \(m\) 易如反掌
  • 若 \(\gcd(g_1-1, N)=pq=N\)
    这意味着 \(g_1-1\equiv 0\pmod{q}\)
    则 \(g_1-1\equiv 0\pmod{N}\)
    \(c_1\equiv m\mod{N}\)，敌手无需找到 \(N\) 的 factorization 即可破解信息 \(m\)

RSA with reused \(m, e\)

Bob 用不同的 \(e_1, e_2\) 加密了相同的信息 \(m\)，其中 \(\gcd(e_1, e_2)=1\)
Eve 截获了这两条密文 \(c_1=[m^{e_1}\mod N], c_2=[m^{e_2}\mod N]\)
请在不找出 \(N\) 的 factorization 的情况下破解 \(m\)

根据 裴蜀定理 (Bezout Identity)，我们有 \(Xe_1+Ye_2=\gcd(e_1, e_2)=1\)
且，通过扩展欧几里得定理可以找到满足条件的一组 \(X, Y\)
计算 \(c_1^Xc_2^Y \mod N\) 即可破解 \(m\):
\(c_1^Xc_2^Y\equiv m^{Xe_1}m^{Ye_2}\equiv m^{Xe_1+Ye_2}\equiv m\pmod{N}\)

More generally, if Bob encrypts a single message using several exponents \(e_1, e_2,...,e_n\), then Eve can recover the plaintext if \(\gcd(e_1, e_2, ..., e_n)=1\).
The moral is that Alice should use at most one encryption exponent for a given modulus.

Public Key Encryption

Adapted El Gamel Encryption

这道题没见过真有点想不出来吧......

• 发现 \(c_2=h^r+m_b\) 使用了 \(+\)，不属于 \(G\) 的群运算，因此 it's not necessary that \(c_2\in G\)
• 然而，由于 \(h^r\in G\)，我们能够保证 \([c_2-m_b\mod{p}]\in G\)
• 根据题意 \(p-1=2q\)，即 \(|\Z_p^*|=2|G|\) (这来自结论：对于奇质数 \(p\) 与集合 \(\{1,2,...,p-1\}\)，集合中模 \(p\) 的二次剩余与二次非剩余数量相等)
  又 \([c_2-m\mod{p}] \in \Z_p^*\) (严格来说是 \(\Z_p\)，但是 \([c_2-m\mod{p}]=0\) 不可能成立)
  因此，对于随机的 \(m\)，\([c_2-m\mod{p}]\in G\) 的概率是 \(1/2\)
• 对于敌手输出的 \(m_0, m_1\)，挑战者选择加密 \(m_b\):
  那么 \(\Pr[[c_2-m_b\mod{p}]\in G]=1\), 而 \(Pr[[c_2-m_{1-b}\mod{p}]\in G]=1/2\) (\(m_{1-b}\) 是随机选取的)
• 敌手只需要分别计算上式，若 \([c_2-m_0\mod{p}]\in G\)，输出 \(0\); 若 \([c_2-m_1\mod{p}]\in G\)，输出 \(1\); 若两者都 \(\in G\)，则输出一个 random guess
  敌手获得胜利的概率是 \(\Pr[\mathtt{PubK}^{\mathtt{eav}}_{\Pi, \mathscr{A}}(n)=1]=1/2+1/2\times 1/2=3/4\)

\(3/4\) 并不是一个可忽略的概率，因此这个加密方案不是 CPA-secure 的

One-way Function

Hard-Core Predicates and Pseudorandom Generators

之前提过，one-way function 并不能保证部分信息的泄露，其就算有硬核谓词也只保证有一部分信息不会泄露

\(G(x_1, x_2)\) 很明显是一个单向函数:
前半部分保证了 \(x_1\) 的单向性 (硬核谓词 \(hc(x_1, x_2)\) 只能从单向函数 \(g\) 上下手了)
后半部分是 \(n/2\) 个连续的 \(0\)，保证了 \(x_2\) 的信息绝不会被泄露 (结果根本就与 \(x_2\) 无关)
然而，由于这 \(n/2\) 个 \(0\) 的存在，可以很容易将其与 random string 区别开，因此其不能作为 PRG

PRG and One-Way Function (?)

上一道题目要求我们证明某个 one-way function 不是 PRG，这一题要求我们证明某个 PRG 是 one-way function、
虽然这两个概念之间有着千丝万缕的联系，但是两者之间并不存在绝对的共存/不共存关系
老样子，我们构建 reduction: 外层 \(\mathscr{S}\) 是 PRG 敌手，进行 PRG 不可分辨实验；内层 \(\mathscr{A}\) 是 one-way function 敌手，进行 \(\mathtt{Invert}\) 实验

• PRG 挑战者 \(\mathscr{C}\) 给出 \(r \ (|r|=n+1)\)，其中 \(r\) 等概率的在 \(r\leftarrow U_{n+1}\) 与 \(r:=G(s) \ (s\leftarrow U_n)\) 中选取
• \(\mathscr{S}\) invokes \(\mathscr{A}(1^n, r)\)
• \(\mathscr{A}\) 返回 \(s'\) (\(r\) 的 preimage)
• \(\mathscr{S}\) 计算 \(G(s')\): 若 \(G(s')=r\) 输出 \(1\), 反之输出一个 random guess

整个归约过程中最难理解的应该是最后一步：若 \(G(s')\neq r\)，并不输出 \(0\) 而是输出 random guess

• 若 \(r:=G(s) \ (s\leftarrow U_{n})\)
  \(\Pr[\mathscr{S}(G(s))=1]=\Pr[G(s')=r]+1/2 \Pr[G(s')\neq r]\)
  设敌手 \(\mathscr{A}\) 在 \(\mathtt{Invert}\) 实验中胜利的概率为 \(\epsilon(n)\), 则 \(\Pr[G(s')=1]=\Pr[\mathtt{Invert}_{\mathscr{A}, G}(1^n)=1]=\epsilon(n)\)
  所以 \(\Pr[\mathscr{S}(G(s))=1]=\epsilon(n)+1/2(1-\epsilon)=1/2+1=\epsilon(n)/2\)
• 若 \(r\leftarrow U_{n+1}\)
  \(\Pr[\mathscr{S}(r)=1]=\Pr[G(s')=r]+1/2\Pr[G(s')\neq r]\)
  对于 uniform \(r\leftarrow U_{n+1}\), 一共有 \(2^{n+1}\) 种不同的 \(r\)
  而对于 \(G(s)\)，由于 \(G\) 是 determinisic 且 \(s\leftarrow U_{n}\), 所以最多有 \(2^n\) 种不同的 \(G(s)\)
  令 \(p\) 为 \(G(s)\) 占 \(r\) 中的比例，则有 \(p\leq 2^n/2^{n+1}=1/2\)
  所以对于一个随机选取的 \(r\)，概率为 \(p\) 存在 \(r:=G(s)\)，而 \(\mathscr{A}\) 输出 \(s\) 的概率为 \(\epsilon(n)\)，即 \(\Pr[G(s')=r]=p\epsilon(n), p\leq1/2\)
  \(\Pr[\mathscr{S}(r)=1]=p\epsilon(n)+1/2(1-p\epsilon(n))=1/2+p\epsilon(n)/2, p\leq 1/2\)

综上，以及 \(G\) 是一个 PRG，存在 negligible 概率 \(neg(n)\)，满足
\(|\Pr[\mathscr{S}(G(s))=1]-\Pr[\mathscr{S}(r)=1]|=\frac{(1-p)\epsilon(n)}{2}\leq neg(n)\)
所以 \(\epsilon(n)=\frac{2neg(n)}{1-p}\)
\(\frac{2}{1-p}\) 是一个范围确定的常数，所以 \(\epsilon(n)\) 同样是 negligible 的
因此 \(\Pr[\mathtt{Invert}_{\mathscr{A}, G}(1^n)=1]=\epsilon(n)\) for a negligible \(\epsilon(n)\)，\(G\) 是 one-way function

Nested One-Way Function

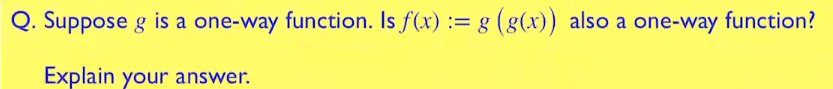
有点反直觉，但是答案是 No!
若 \(g'(x)\) 是一个 one-way function，\(g'(x): \{0,1\}^n\to\{0,1\}^n\)
我们构造 \(g(x): \{0,1\}^{2n}\to\{0,1\}^{2n}\) 为 \(g(x)=g(x_1, x_2)=g'(x_2)||0^{n}\)
这样，\(f(x)=g(g(x))=g(g'(x_2), 0^{n})=g'(0^n)||0^n\)
在该构造下，\(f(x)\) 是一个常数函数，也就是说，对于任意 \(x_1,x_2\in\{0,1\}^n\)，都有 \(f(x_1,x_2)=g'(0^n)||0^n\)
所以 \(f\) 不是 one-way function，其 preimage 可以是任意的 \(x_1, x_2\in\{0,1\}^n\)

Hash Functions and One-Way Functions

(本质上是由哈希函数的 collision resistance 证明 preimage)

很简单的 reduction，\(\mathscr{A}'\) 是哈希冲突敌手，\(\mathscr{A}\) 是单向函数敌手，尝试 invert (即找出 \(y=H^s(x)\) 的原像)

这道题的重点在于，\(\mathscr{A}\) invert 得到的原像 \(x'\) 是否等于 \(x\)
\(H: \{0,1\}^{2n}\to \{0,1\}^n\)，我们将 \(2^{2n}\) 个 \(x\) 分为若干组原像，每一组中的 \(H^s(x)\) 对应的 \(y\) 都相同

• Bad cases:
  我们用 \(Bad_s\) 表示所有 \(x\in\{0,1\}^{2n}\), 满足 \(y=H^s(x)\in\{0,1\}^n\) 的原像数量 \(\leq 2^{\gamma n} \ (\gamma < 1)\)
  则 \(Bad_s\) 包含所有大小 \(\leq 2^{\gamma n}\) 的原像组：由于 \(y\in\{0,1\}^n\)，这样的原像组最多有 \(2^n\) 个
  \(|Bad_s|\leq 2^n\cdot 2^{\gamma n}=2^{(1+\gamma)n}\)

当 \(x\in Bad_s\) 时，\(\Pr_{x\leftarrow \{0,1\}^{2n}}[x\in Bad_s]\leq 2^{(1+\gamma)n}/2^{2n}=2^{(\gamma-1)n}\)
由于 \(\gamma<1\)，这一概率是 negligible 的

• Good cases:
  若 \(x\in Good_s\)，则 \(H^s(x)\) 对应的原像 \(> 2^{\gamma n}\) 个
  则 \(\mathscr{A}\) 返回的原像 \(x'\neq x\) 的概率是 \((1-\frac{1}{2^{\gamma n}})\)

那么 \(\Pr[Hash^{col}_{H, \mathscr{A}'}(n)=1]=\Pr[Hash^{col}_{H, \mathscr{A}'}(n)=1|x\in Bad_s]\Pr[x\in Bad_s]+\Pr[Hash^{col}_{H, \mathscr{A}'}(n)=1|x\in Good_s]\Pr[x\in Good_s]\)

\(\Pr[x\in Bad_s]\) 是 negligible 的；
相反的，\(\Pr[x\in Good_s]=1-\Pr[x\in Bad_s]\)，因此 \(\Pr[x\in Good_s]\) 是 non-negligible 的
\(\Pr[Hash^{col}_{H, \mathscr{A}'}(n)=1|x\in Good_s]=(1-\frac{1}{2^{\gamma n}})\Pr[Inv_{H, \mathscr{A}}(n)=1]\)，而其中的 \((1-\frac{1}{}2^{\gamma n})\) 是 non-negligible 的
由于 \(H\) 是 collision-resistant 的，因此 \(\Pr[Hash^{col}_{H, \mathscr{A}'}(n)=1]\) 是 negligible 的

那么我们有 \(neg=neg+nonneg\cdot \Pr[Inv_{H, \mathscr{A}}(n)=1] \cdot nonneg\)，可以推出 \(\Pr[Inv_{H, \mathscr{A}}(n)=1]\) 一定是 negligible 的
所以 \(H\) 是 one-way function 得证

Hash Functions

Exercise: Hash Functions based on Number-Theoretic Primitives

这题真有点难
我们用以下的方法证明当 \(H^s\) 出现冲突时，能够 efficiently 计算 \(y\) 的 \(e\)-th root
首先，研究一下函数 \(f\): 举几个例子来理解

• 对于数列 \(\{101\}\): 由里到外计算 \(H^s(x)=y((y\cdot 1^e)^e)^e=y^{e^2+1}\)，括号由里到外分别是 \(y^1(1), y^{e}(10), y^{e^2+1}(101)\)
• 对于数列 \(\{111\}\): 由里到外计算 \(H^s(x)=y\cdot(y\cdot(y\cdot 1^e)^e)^e=y^{e^2+e+1}\)，括号由里到外分别是 \(y(1), y^{e+1}(11), y^{e^2+e+1}(111)\)

我们定义函数 \(F_i:=f_{x_i}^s(F_{i-1})\), \(F_0=1\)
\(F\) 即是在计算 \(H^s\) 时，每一次拆括号时所得到的数值，例如对于数列 \(\{101\}\), \(F_0=1, F_1=y^1, F_2=y^e, F_3=y^{e^2+1}\)
对于 \(x\in\{0,1\}^{3n}\), \(H^s(x)=F_{3n}(x)\)

当 \(H\) 发生 collision 时，存在 \(H^s(x)=H^s(z)\)，即 \(F_{3n}(x)=F_{3n}(z)\)
由于最终的结果 \(F_{3n}(x)=F_{3n}(z)\), 想象 \(F_i(x)\) 与 \(F_i(z)\) 两个数列，在由 \(1\) 到 \(3n\) 逐步产生的过程中，一定存在某个位置 \(j<3n\)，使得
\(F_j(x)\neq F_j(z)\) 而 \(F_{j+1}(x)=F_{j+1}(z)\)
因为 \(F_{j+1}(x)=f_{x_j}^s(F_j(x)), F_{j+1}(z)=f_{z_j}^s(F_j(z))\)
由于 \(F_{j+1}(x)=F_{j+1}(z)\)，而 \(F_j(x)\neq F_j(z)\)，且函数 \(f\) 是 deterministic 的，可以得出结论 \(f_{x_j}^s\) 与 \(f_{z_j}^s\) 是两个不同的函数
即 \(x_j\neq z_j\)
我们不妨设 \(x_j=0, z_j=1\)，则 \(f_0^s(F_j(x))=f_1^s(F_j(z))\)
那么 \(F_j(x)^e=y\cdot F_j(z)^e\), 整理有 \(y=F_j(x)^eF_j(z)^{-e}\)
由此推出 \(y\) 的 \(e\)-th root \(y^{1/e}=F_j(x)F_j(z)^{-1}\mod{N}\)
由于 \(H^s\) 是 PPT 算法，因此计算 \(F_i\) 也是 efficient 的
所以，若对于 GenRSA, RSA 问题是困难的，则哈希函数 \(H\) 是 collision-resistant 的

Public-Key Encryption

Public-Key Encryption and Key-Exchange Protocol

这题意我还理解了半天：这里的 simulate Alice 可以理解为将 Alice 作为其子程序
这个题目提供了一种通用的方法：对于任意的 Key-Exchange Protocol 构建一个 Public Key Encryption

对于 key-exchange protocol 而言，其安全性是由实验 \(KE^{eav}\) 定义的: 敌手在给定 transcript 的情况下，无法分辨密钥 \(k\) 与任意随机串
我们构建 proof of reduction，构建 KE 不可分辨实验的敌手 \(A\)，使用公钥加密敌手 \(A'\) 作为其子程序

这道题的重点：

• \(KE^{eav}\) 实验的定义
  敌手获得了公钥交换中的 transcript ( 在类似 Diffie-Hellman 的 2-round key-exchange 中，获得 \((t_1, t_2)\) ) 与串 \(r\)
  若敌手能够分辨 \(r\) 是公钥还是某个随机串，那么敌手胜利

• 公钥加密的 CPA 安全
  由于公钥加密中的敌手能够获得公钥 \(pk\)，相当于获得了 \(Enc(\cdot)\) 的 oracle access
  所以公钥加密的 CPA 安全与 EAV 安全等价

• 密钥交换协议与公钥加密
  搞清楚他们之间的联系与区别 (因为这一点没捋清楚想了很久)

  • 密钥交换协议：
    Bob 与 Alice 双方通过交换信息 ( 即 \(\mathtt{trans}\) transcript )，共同设立了密钥 \(k\)
    (这一密钥 \(k\) 可接下来可作为其他单钥加密的密钥，但这样的加密并不是公钥加密，而是密钥交换+单钥加密)
    敌手进行 \(\mathtt{KE}^{eav}\) 实验：在得到 \(\mathtt{trans}\) 的情况下，能否成功分辨密钥 \(k\) 与某个随机串
  • 公钥加密
    Alice (作为 receiver) 生成公钥 \(pk\) 与私钥 \(sk\)，其中公钥 \(pk\) 被公布 ( 一般包括 \((G,q,g,h)\) )
    Bob (作为 sender) 使用公钥 \(pk\) 加密信息，Alice 使用私钥 \(sk\) 解密
    由这里可以看出公钥加密与密钥交换+单钥加密的不同之处：其密钥的分布一定是 非对称 (asymmetric) 的
    而密钥交换+单钥加密的本质仍是单钥加密，其密钥的分布是对称 (symmetric) 的

构建 reduction:

接下来的概率分析就比较简单了

Malleability of El Gamel Encryption Scheme

在 El-Gamel 中，公钥 \(pk=(G, q, g, h=g^{x})\)，私钥 \(sk=x\)
sender 将随机选择 \(y\)，密文 \(c=(g^y, g^{xy}\cdot m)\)

对于某个密文 \(c=(c_1=g^y, c_2=g^{xy}\cdot m)\)，我们这样进行修改
随机生成 \(r\)，计算 \(c_1'=c_1\cdot g^r=g^{r+y}\), \(c_2'=c_2\cdot h^r=g^{xy+xr}m=g^{x(r+y)}m\)
仍然符合 \((c_1')^x m=c_2'\)
所以新的 \(c'=(c_1', c_2')=(g^r c_1, \alpha h^r c_2)\)

\(r\) 的随机性使得 \(c'\) 与 \(c\) 是 完全独立 (independent) 的，\(c'\) 可视为对信息 \(\alpha m\) 的随机加密，与 \(c\) 无关